正交匹配追踪 OMP 算法原理分析

小序：           

           最近研究OMP贪婪迭代算法找了Rachel-Zhang的一篇博客《“压缩感知” 之 “Hello World” 》    里面讲到了作者对OMP算法的理解，看完之后有所启发但是有些地方依然不理解，毕竟大牛作者不喜说的很详细，菜鸟看不懂也很常见，所以自己查了一些资料，这里做个更详细的分析，仅供菜鸟分享。

        上文地址为：http://blog.csdn.net/abcjennifer/article/details/7775284    

        另外本人硕士课题方向为压缩感知框架下多模板的超宽带信道估计，有同道的朋友可以共同交流

正文：

           代码作者为香港大学电子工程系沙威，发送信号x为若干个不同周期的正弦波的线性叠加，且假定了接收端与发射端之间无噪声

程序运行结果：  蓝色为原始信号，红色为恢复信号，可见该算法可以高精度的恢复原始信号。

.

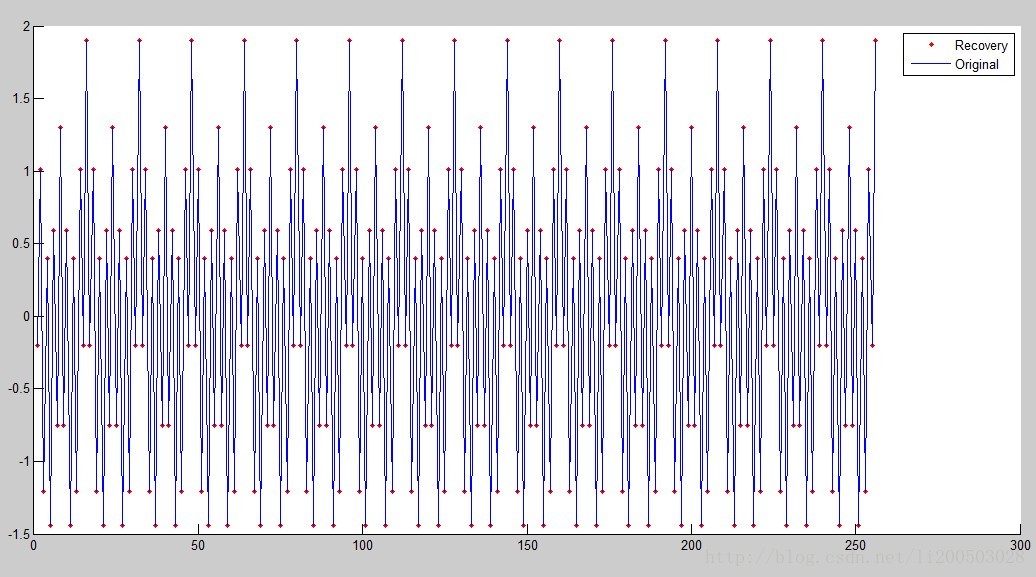
下面介绍Orthogonal Matching Pursuit 算法：

        正交匹配追踪算法迭代的基本思想就是每次迭代过程中从全息矩阵T中选出与测量信号s相关度（内积）最大的那一列，然后从T中去掉该列并加入到扩充矩阵Aug_t中，然后利用最小二乘法原理求出使残差r_n=s-Aug_t*aug_y最小的一个估计aug_y，然后不断的从T中减去相关列重复以上过程，直到达到迭代次数m结束。

        本人开始不理解为什么最小二乘法的求出的估计量就会使残差最小，于是查阅最小二乘法原理如下：

仔细看过推到那想必就会理解式aug_y=(Aug_t'*Aug_t)*Aug_t'*s为什么能得到最优解了，那么我们所说的最小残差r_n=s-Aug_t*aug_y  也就合理了       

          下面OMP代码的按行分析

 for times=1:m;                                         

    for col=1:N;                                             搜寻恢复矩阵的所有列向量
        product(col)=abs(T(:,col)'*r_n)/(T(:,col)'*T(:,col));           找出该矩阵中与残差相关度最大的那一列

    end
     [val,pos]=max(product);                          最大投影系数对应的位置

    Aug_t=[Aug_t,T(:,pos)];                           相关度最大的那一列加入到扩充矩阵Aug_t   

    T(:,pos)=zeros(M,1);                                选中的最大列置零  

   aug_y=(Aug_t'*Aug_t)*Aug_t'*s;               最小二乘,使残差最小  该处假设正在迭代第k次那么  

                                                                                     aug_y（k*1维）=（Aug_t'（k*N维） * Aug_t（N*k维））*  Aug_t'（k*N维） *   s（N*1维）

     r_n=s-Aug_t*aug_y;                              残差 

    pos_array(times)=pos;                            纪录最大投影系数的位置
end
hat_y(pos_array)=aug_y;                            重构的谱域向量       最后一次迭代生成的aug_y（m*1维）按照 pos_array排列之后就是想到的恢复信号hat_y
hat_x=real(Psi'*hat_y.');                              

最后

以上就是懵懂网络为你收集整理的正交匹配追踪 OMP 算法原理分析的全部内容，希望文章能够帮你解决正交匹配追踪 OMP 算法原理分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。