目录
- 1. 原理详解
- 1.1. 线性回归
- 1.2. 回归系数
- 2. 公式推导
- 2.1. 单元线性回归
- 2.2. 多元线性回归
- 3. 简单实例
- 3.1. 实例1：一元线性回归
- 实例2： 多元线性回归
- 3.3. 实例3：房价预测
1. 原理详解
1.1. 线性回归
假设一个空间中有一堆散点，线性回归的目的就是希望用一条直线，最大程度地“概括”这些散点。它不要求经过每一个散点，但是希望能考虑到每个散点的特点。按照西瓜书的例子就是，好瓜的评判标准y可以由
x
i
x_i
xi表示，也就是说，
f
g
o
o
d
(
x
)
=
w
1
x
色泽
+
w
1
x
根蒂
+
w
1
x
敲声
+
b
f_{good}(x)=w_1x_{色泽}+w_1x_{根蒂}+w_1x_{敲声}+b
fgood(x)=w1x色泽+w1x根蒂+w1x敲声+b。
那么我们不难发现，线性回归需要考虑的几个问题：
- 确定系数 w i w_i wi以及偏置 b b b
- 如何确定 f g o o d ( x ) f_{good}(x) fgood(x)能很好地概括瓜的特点
1.2. 回归系数
关于这点，我们需要确定，我们算出来的回归系数一定是当前最优的结果，怎么确定呢？
- 均方误差（西瓜书）
- R^2（用于模型评估）
均方误差（MSE）
这个其实就是残差平方和的平均值。
M
S
E
=
∑
i
=
0
n
y
i
−
f
(
x
i
)
n
MSE=frac{sum_{i=0}^ny_i-f(x_i)}{n}
MSE=n∑i=0nyi−f(xi)
R^2
R 2 = S S R S S T = S S T − S S E S S T = 1 − S S E S S T R^2=frac{SSR}{SST}=frac{SST-SSE}{SST}=1-frac{SSE}{SST} R2=SSTSSR=SSTSST−SSE=1−SSTSSE
其中，SST是总偏差平方和
S
S
T
=
∑
i
=
0
n
(
y
i
−
y
ˉ
)
2
SST=sum_{i=0}^n(y_i-bar y)^2
SST=i=0∑n(yi−yˉ)2
SSR是回归平方和
S
S
R
=
∑
i
=
0
n
(
f
(
x
i
)
−
y
ˉ
)
2
SSR=sum_{i=0}^n(f(x_i)-bar y)^2
SSR=i=0∑n(f(xi)−yˉ)2
SSE是残差平方和
S
S
E
=
∑
i
=
0
n
(
y
i
−
f
(
x
i
)
)
2
SSE=sum_{i=0}^n(y_i-f(x_i))^2
SSE=i=0∑n(yi−f(xi))2
2. 公式推导
2.1. 单元线性回归
这里我们跟西瓜书一样采取均方误差。
计算得w与b。
2.2. 多元线性回归
多元线性回归涉及到矩阵运算。
若X为m * n的矩阵，则 X T X X^TX XTX为n * n的方阵。 X T X X^TX XTX的意义在于保持其为可逆矩阵，因为若它不可逆，则导致其行列式为0，就会导致w趋向无穷。
3. 简单实例
3.1. 实例1：一元线性回归
计算这个二元线性回归
| index | x | y |
|---|---|---|
| 1 | 6 | 2 |
| 2 | 8 | 1 |
| 3 | 10 | 0 |
| 4 | 14 | 2 |
| 5 | 18 | 0 |
我们这里采用几种解法
- 西瓜书内的公式
- 最小二乘估计w, b
- linalg直接解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60# -*- coding:utf-8 -*- # 2022.09.05 import matplotlib.pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D def task1_vis(x, y, w, b): fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.scatter(x, y) x = np.linspace(0, 20, 100) y = w * x + b ax.plot(x, y) # plt.title('Pizza price plotted against diameter') ax.set_xlabel('x', fontdict={'size': 10, 'color': 'black'}) ax.set_ylabel('y', fontdict={'size': 10, 'color': 'black'}) plt.show() def task1_way1(x, y): w = np.dot(y, (x - x.mean())).sum() / (sum(np.square(x)) - np.square(sum(x)) / x.shape[0]) b = sum(y - np.multiply(w, x)) / x.shape[0] print("方法一：ttw：{}tb：{}".format(w, b)) def task1_way2(x, y): x_bar = x.mean() y_bar = y.mean() # 计算协方差 cov = np.multiply((x - x_bar).transpose(), (y - y_bar)).sum() / (x.shape[0] - 1) var = np.var(x, ddof=1) w = cov / var # w = (y_bar - w * x_bar) / (x.shape[0]) b = y_bar - w * x_bar print("方法二：ttw：{}tb：{}".format(w, b)) def task1_way3(x, y): from numpy.linalg import lstsq x = np.vstack([x, [1 for i in range(x.shape[0])]]) w = lstsq(x.T, y.reshape(-1, 1))[0][0][0] b = lstsq(x.T, y.reshape(-1, 1))[0][1][0] print("方法三：ttw：{}tb：{}".format(w, b)) return w, b def task1(): x = np.array([6, 8, 10, 14, 18]) y = np.array([7, 9, 13, 17.5, 18]) task1_way1(x, y) task1_way2(x, y) w, b = task1_way3(x, y) task1_vis(x, y, w, b) if __name__ == '__main__': task1()
运行结果如下
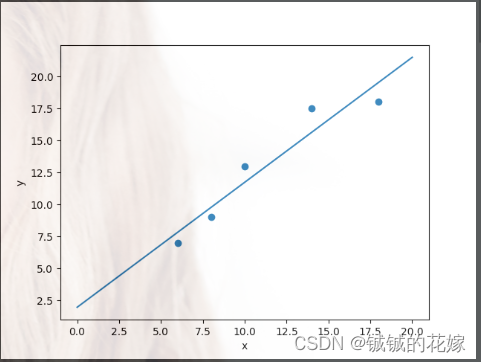
实例2： 多元线性回归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20# -*- coding:utf-8 -*- import matplotlib.pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D def task2(): from numpy.linalg import inv X = np.array([[1, 6, 2], [1, 8, 1], [1, 10, 0], [1, 14, 2], [1, 18, 0]]) X[:, 2] = X[:, 1] * X[:, 1] Y = np.array([[7], [9], [13], [17.5], [18]]) beita = np.dot(inv(np.dot(np.transpose(X), X)), np.dot(np.transpose(X), Y)) print(beita) from numpy.linalg import lstsq print(lstsq(X, Y)[0]) if __name__ == '__main__': # task1() task2()
3.3. 实例3：房价预测
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83# -*- coding:utf-8 -*- # 2022.09.05 import matplotlib.pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D def task1_vis(x, y, w, b): fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.scatter(x, y) y = w * x + b ax.plot(x, y, 'r') # plt.title('Pizza price plotted against diameter') ax.set_xlabel('x', fontdict={'size': 10, 'color': 'black'}) ax.set_ylabel('y', fontdict={'size': 10, 'color': 'black'}) plt.show() def task1_way1(x, y): w = np.dot(y, (x - x.mean())).sum() / (sum(np.square(x)) - np.square(sum(x)) / x.shape[0]) b = sum(y - np.multiply(w, x)) / x.shape[0] print("方法一：ttw：{}tb：{}".format(w, b)) return w, b def task1_way2(x, y): x_bar = x.mean() y_bar = y.mean() # 计算协方差 cov = np.multiply((x - x_bar).transpose(), (y - y_bar)).sum() / (x.shape[0] - 1) var = np.var(x, ddof=1) w = cov / var # w = (y_bar - w * x_bar) / (x.shape[0]) b = y_bar - w * x_bar print("方法二：ttw：{}tb：{}".format(w, b)) def task1_way3(x, y): from numpy.linalg import lstsq x = np.vstack([x, [1 for i in range(x.shape[0])]]) w = lstsq(x.T, y.reshape(-1, 1))[0][0][0] b = lstsq(x.T, y.reshape(-1, 1))[0][1][0] print("方法三：ttw：{}tb：{}".format(w, b)) return w, b def task1(): x = np.array([6, 8, 10, 14, 18]) y = np.array([7, 9, 13, 17.5, 18]) task1_way1(x, y) task1_way2(x, y) w, b = task1_way3(x, y) task1_vis(x, y, w, b) def task2(): from numpy.linalg import inv X = np.array([[1, 6, 2], [1, 8, 1], [1, 10, 0], [1, 14, 2], [1, 18, 0]]) X[:, 2] = X[:, 1] * X[:, 1] Y = np.array([[7], [9], [13], [17.5], [18]]) beita = np.dot(inv(np.dot(np.transpose(X), X)), np.dot(np.transpose(X), Y)) print(beita) from numpy.linalg import lstsq print(lstsq(X, Y)[0]) def task3(): x_train = np.array([77.36, 116.74, 116.7, 100.68, 116.1, 115.81, 104.24, 106.73, 115.86]) y_train = np.array([470, 730, 760, 680, 700, 720, 700, 690, 730]) x_test = np.array([56.6, 78.4, 58, 123.5, 56.8, 77, 150.6]) w, b = task1_way1(x_train, y_train) y_pre = x_test * w + b print(y_pre) task1_vis(x_train, y_train, w, b) if __name__ == '__main__': # task1() # task2() task3()
最后
以上就是跳跃康乃馨最近收集整理的关于机器学习之线性回归原理详解、公式推导（手推）、简单实例1. 原理详解2. 公式推导3. 简单实例的全部内容，更多相关机器学习之线性回归原理详解、公式推导（手推）、简单实例1.内容请搜索靠谱客的其他文章。
发表评论 取消回复