本系列是一个基于深度学习的NLP教程，2016年之前叫做CS224d: Deep Learning for Natural Language Processing，之后改名为CS224n: Natural Language Processing with Deep Learning。新版主讲人是泰斗Chris Manning和Richard Socher（这是旧版的讲师），两人分别负责不同的章节。博主在学习的同时，对重点内容做成系列教程，与大家分享！

系列目录（系列更新中）

• 第二讲 cs224n系列之word2vec & 词向量

• word2vec进阶之skim-gram和CBOW模型（Hierarchical Softmax、Negative Sampling）

• 第三讲 cs224n系列之skip-pram优化 & Global Vector by Manning & 词向量评价

1 skip-pram回顾

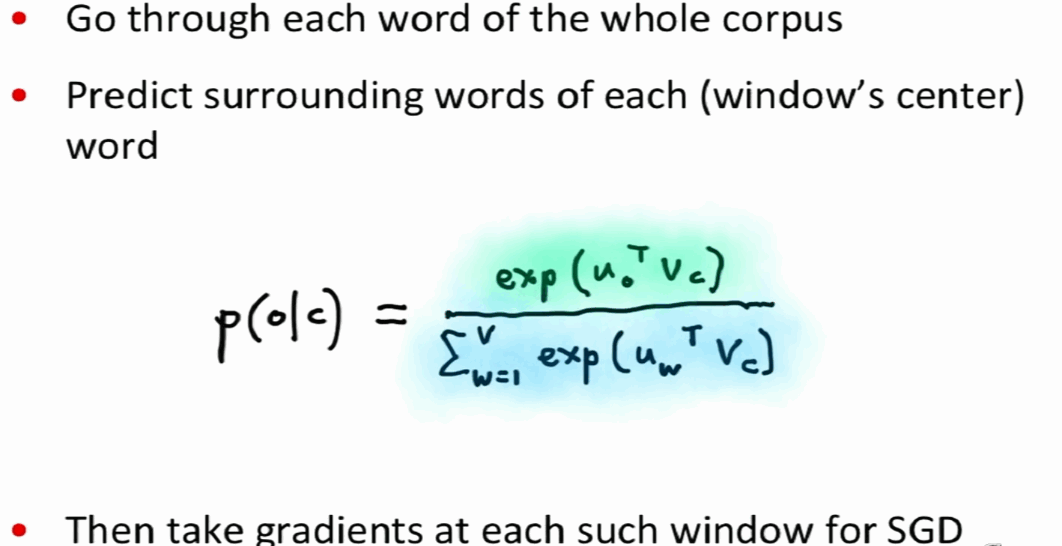$$J_t(theta) = log sigma left ( u_o^Tv_c right ) + sum _ { i=1 } ^k mathbb { E } _ { j sim P ( w ) } left [ log left ( 1- sigma left ( u^T_jv_c right ) right ) right ] $$ 根据公式$1- sigma(lambda)=sigma(-lambda)$ $$J_t(theta) = log sigma left ( u_o^Tv_c right ) + sum _ { i=1 } ^k mathbb { E } _ { j sim P ( w ) } left [ log sigma left (- u^T_jv_c right ) right ] $$

PS：这里的 $ J_t $ 里的t是第t步或者是第t个窗口
到此为止，就可以用tensorflow实现以下skip-pram了，关于skip-pram的tensorflow实现方法教程详见

参考连接链接

---

问答：
如果不是凸函数，这可能会陷入局部最优解，那么初始化就比较关键，但是在实践中，只要是用一个小的随机化初始化，一般不会出现问题。

2 skip-pram优化

在第一部分讲解完成后，我们会发现Word2Vec模型是一个超级大的神经网络（权重矩阵规模非常大）。
举个栗子，我们拥有10000个单词的词汇表，我们如果想嵌入300维的词向量，那么我们的输入-隐层权重矩阵和隐层-输出层的权重矩阵都会有 10000 x 300 = 300万个权重，在如此庞大的神经网络中进行梯度下降是相当慢的。更糟糕的是，你需要大量的训练数据来调整这些权重并且避免过拟合。百万数量级的权重矩阵和亿万数量级的训练样本意味着训练这个模型将会是个灾难（太凶残了）。
相关解决方法就是在skip-pram的基础上优化，主要有如下两种：

• 对高频次单词进行抽样来减少训练样本的个数。
• 对优化目标采用“negative sampling”方法，这样每个训练样本的训练只会更新一小部分的模型权重，从而降低计算负担。

对于这两种方法，我自己的理解是第一种是解决词向量的个数的，也就是one-hot对应词向量矩阵的维数，采用的方法是只构建高频词，换另外一种方式说是减少中心词的个数，也就是对应的 $ V_c $ 的个数，而第二种我认为是从隐层到输出层不会对每个其他的词向量点乘，也就是最后的结果不是和输出对应的那么多维数的向量了，这样就减少了，应该对吧！

以上两种方法详见

参考连接

3 Global Vector by Manning

global vector: Manning

背景

Cbow 或者Skip-Gram取得了很大的成功，不管在训练效率还是在词向量的计算效果上面。
但是考虑到Cbow/Skip-Gram 是一个local context window的方法，比如使用NS来训练，缺乏了整体的词和词的关系，负样本采用sample的方式会缺失词的关系信息。
**另外，直接训练Skip-Gram类型的算法，很容易使得高曝光词汇得到过多的权重 **

Global Vector融合了矩阵分解Latent Semantic Analysis (LSA)的全局统计信息和local context window优势。融入全局的先验统计信息，可以加快模型的训练速度，又可以控制词的相对权重。

概率及表示

首先用符号X来表示词和词之间的表示：
$Xij$：词i在词j的window context里面的次数，同样也是j出现在i window context的次数 (说白了就是，在整个语料库中，单词i和单词j共同出现在一个窗口中的次数。 )
$Xi=\sum kXik$：词i的window context里面的词的总次数
$Pij=P(j|i)=Xij/Xi$: 词j出现在词i 的context里面的概率


这里写图片描述
我们看这个Pij的case：

我们知道solid是ice的形状，gas是steam的状态，如果用概率表示，我们希望
$p(solid|ice)>p(solid|steam)，$
$p(gas|ice)<p(gas|steam)， $
为了数值化这个相对大小，我们引入他们的比例：p(k|ice)/p(k|steam), 这个比例值越大，代表词和ice更加相关，比例的值越小，代表和steam更加相关。

下一步：$PikPjk=p(k|i)/p(k|j) $在机器学习里面怎么计算？

最终的公式是：
$$J(\theta )=\frac{1}{2}\sum _{i,j=1}^{W}f(P_{ij}){\left(u_i^T{v}_j-\log P_{ij}\right)}^2$$
这里的$P_{ij}$是两个词共现的频次，相当于上面的$X_{ij}$f是一个max函数,

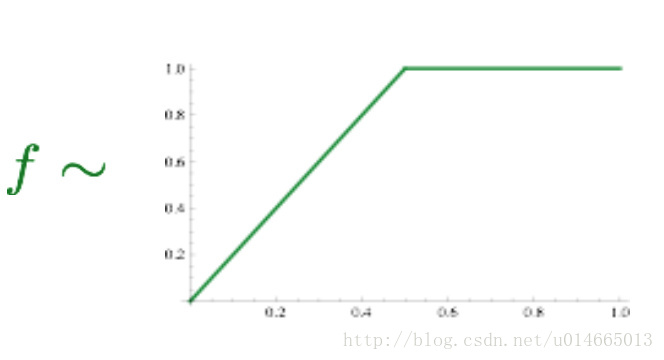
优点是训练快，可以拓展到大规模语料，也适用于小规模语料和小向量。
相对于word2vec只关注窗口内的共现，GloVe这个命名也说明这是全局的（我觉得word2vec在全部语料上取窗口，也不是那么地local，特别是负采样）。

4.词向量评价（Evaluate word vectors）

有了上面的一些算法，但是如何评价运行结果，模型中我们有很多超参数，比如窗口设置多大？词向量的大小如何设置？我们该如何选择这些参数让我们的模型运行的更好

有两种方法：Intrinsic（内部） vs extrinsic（外部）

Intrinsic：专门设计单独的试验，由人工标注词语或句子相似度，与模型结果对比。好处是是计算速度快，但不知道对实际应用有无帮助。有人花了几年时间提高了在某个数据集上的分数，当将其词向量用于真实任务时并没有多少提高效果，想想真悲哀。

Extrinsic：通过对外部实际应用的效果提升来体现。耗时较长，不能排除是否是新的词向量与旧系统的某种契合度产生。需要至少两个subsystems同时证明。这类评测中，往往会用pre-train的向量在外部任务的语料上retrain。

Intrinsic word vector evaluation

也就是词向量类推，或说“A对于B来讲就相当于C对于哪个词？”。这可以通过余弦夹角得到：

这种方法可视化出来，会发现这些类推的向量都是近似平行的：

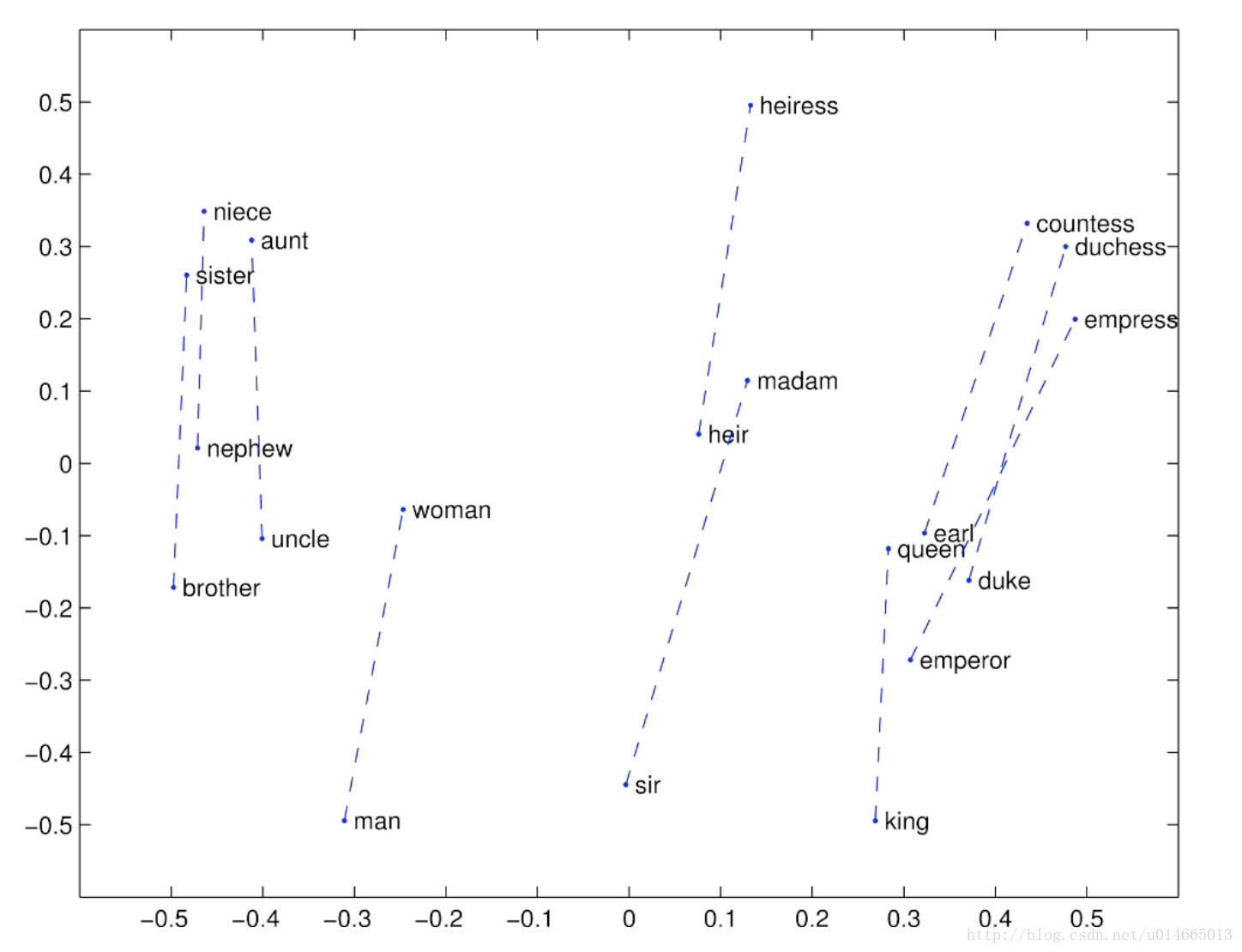
下面这张图说明word2vec还可以做语法上的类比：

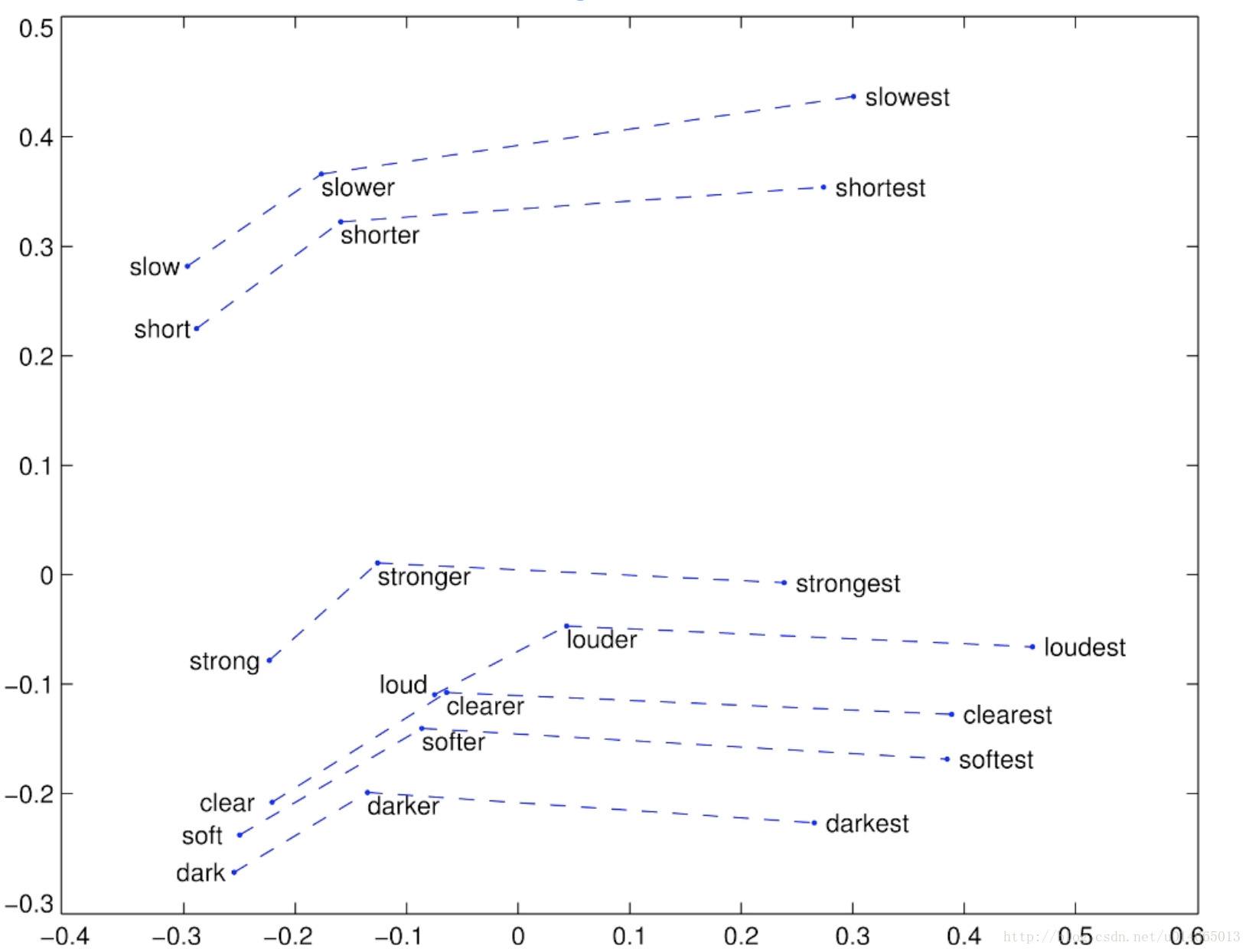
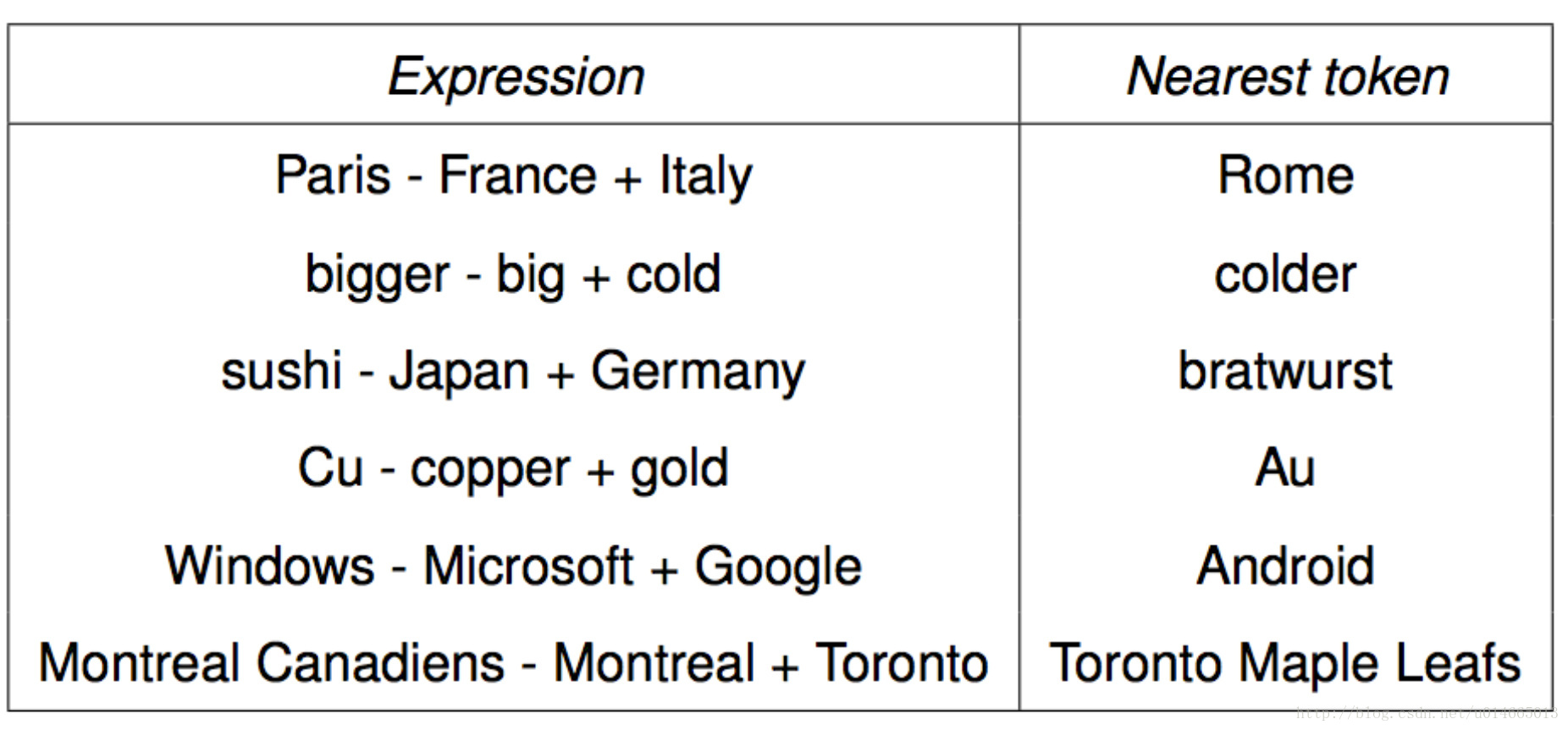
我感觉上面的这种就类似于下面的这种运算，很有意思：

4.1 调参

几个参数的对比：

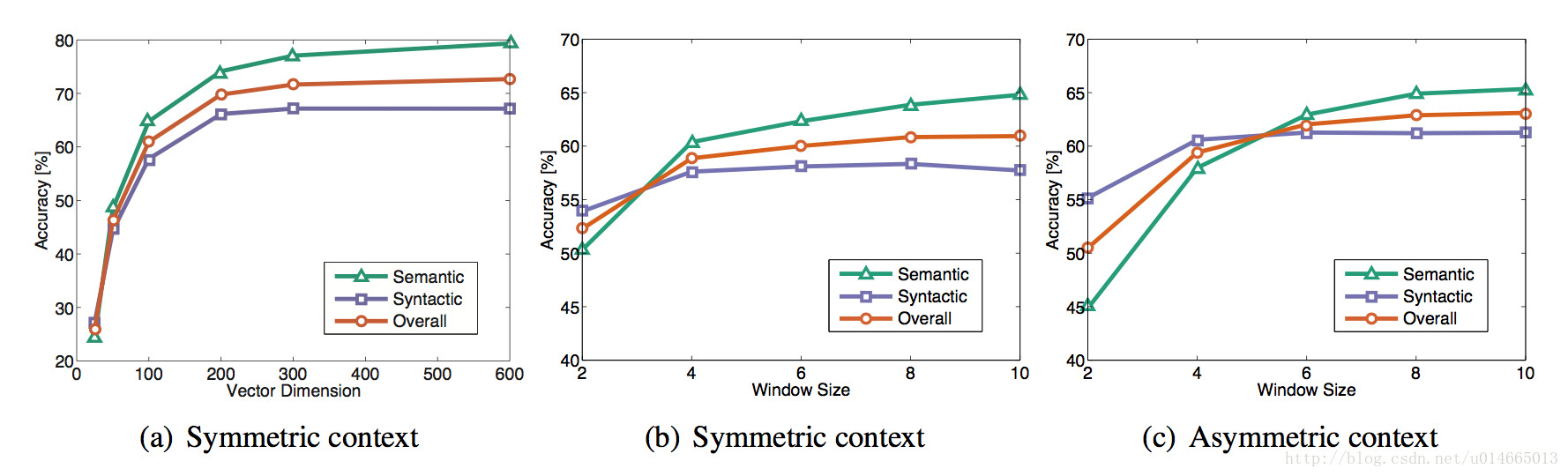
两种模型间的对比：

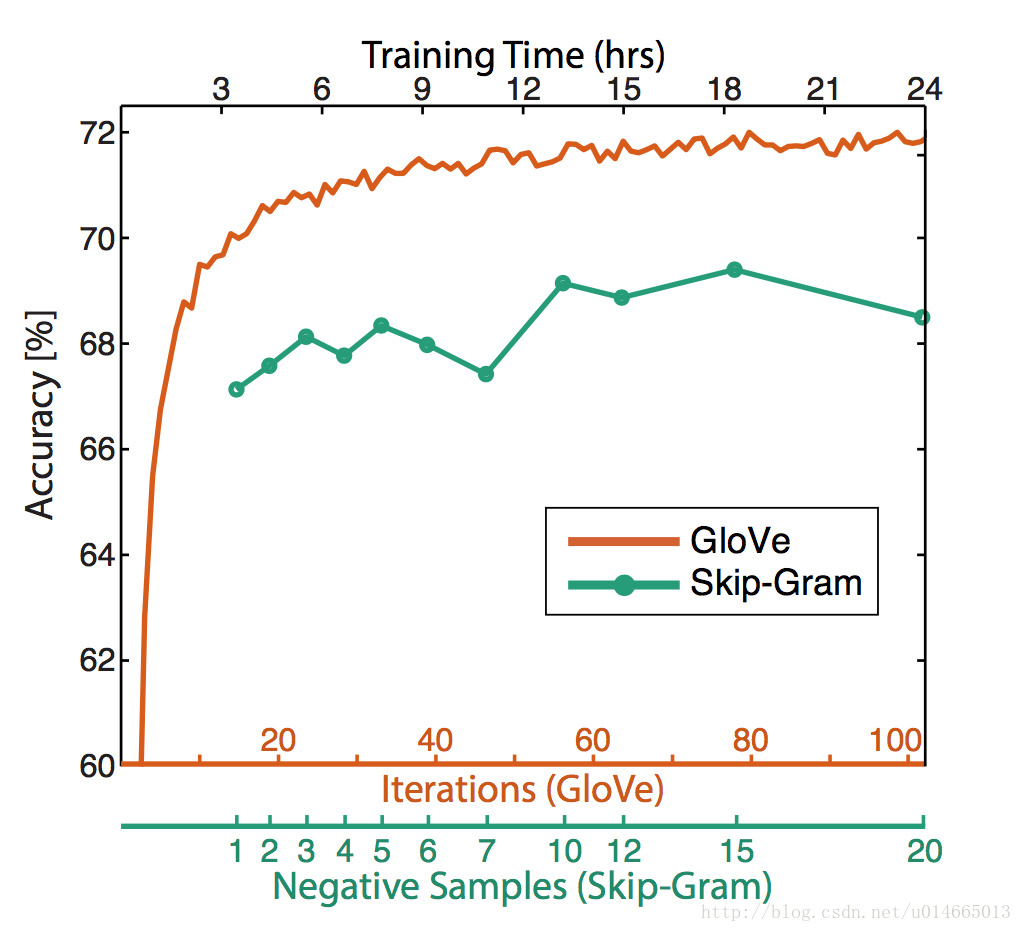
视频中还有很对其他的对比，目前感觉作用不大。

这是是评估，但不是最小化。

参考资料

• CS224n笔记3 高级词向量表示
• cs224n自然语言处理与深度学习简介
• Word Vector的综述
• word2vec原理推导与代码分析
• 各个assignment

相关概念辅助：

• 欧氏距离和余弦相似度的区别是什么？
• 奇异值分解(SVD)
• 交叉熵代价函数（作用及公式推导）

最后

以上就是谦让金针菇为你收集整理的第三讲 cs224n系列之skip-pram优化 & Global Vector by Manning & 词向量评价系列目录（系列更新中）1 skip-pram回顾2 skip-pram优化3 Global Vector by Manning4.词向量评价（Evaluate word vectors）参考资料的全部内容，希望文章能够帮你解决第三讲 cs224n系列之skip-pram优化 & Global Vector by Manning & 词向量评价系列目录（系列更新中）1 skip-pram回顾2 skip-pram优化3 Global Vector by Manning4.词向量评价（Evaluate word vectors）参考资料所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。