Human language and word meaning

语言是一个低带宽的信息传输方式，相比于5G，这决定了语言的熵会很高。

How do we have usable meaning in a computer?

one-hot的字词表示：

1. 词语维度是很高的，而且有很多衍生的词语，接近于无限的维度。
2. 词语之间没有相似度，即one-hot向量是正交的，相似词语和不相似词语之间都是正交关系。

WordNet

一个工具，来获取词语的同义词、hypernyms ( is a relation, eg. panda is a procyonid, ), 缺点：

1. 缺少细微差别
   1. 例如，某些情况下，proficient才是good的同义词，即特定的上下文。
2. 缺少新词，难以实时更新：
3. 主观、需要人力创建和修改，不能计算词语相似度。

分布式表达

使用词语周围的词语来表示其的意义。

Distributional semantics: A word’s meaning is given by the words that frequently appear close-by 、

使用此种方式训练神经网络得到词向量表达，并将其降维到2D，可视化的效果：

可以看到，are, is, were距离很近，向量相似度较高，而实际也是如此。

那么，问题来，怎么训练词向量呢？

Word2vec introduction

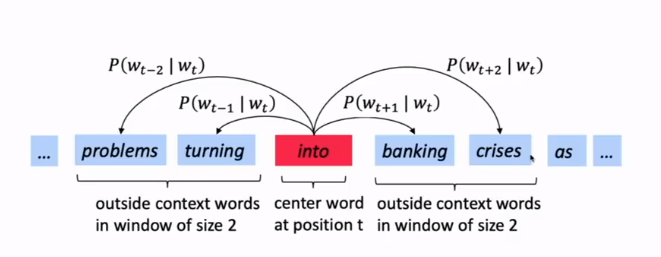
skip-gram：使用中心词语，来预测周围的词语。

最大化似然，目标是对于正确的上下文的词语，给出概率最大, $\theta$是参数：
$$Likelihood=L(\theta )=\prod _{t=1}^T\prod _{\genfrac{}{}{0ex}{}{-m\le j\le m}{j̸=0}}P\left(w_{t+j}|w_t;\theta \right)$$
目标函数，注意加了负号，所以是最小化目标函数 ：
$$J(\theta )=-\frac{1}{T}\log L(\theta )=-\frac{1}{T}\sum _{t=1}^T\sum _{\genfrac{}{}{0ex}{}{-m\le j\le m}{j̸=0}}\log P\left(w_{t+j}|w_t;\theta \right)$$
那么如何计算概率$P(w_{i+j}|w_t;\theta )$?

1. 对于每个词语都有两个向量：
   • w作为中心词的向量$v_w$
   • w作为上下文的向量$u_w$
2. 对于中心词语c，上下文词语o：

$$P(o|c)=\frac{\exp \left(u_o^T{v}_c\right)}{{\sum }_{w\in V}\exp \left(u_w^T{v}_c\right)}$$

那么，参数空间为$\theta \in R^{2d\ast v}$，其实就是词向量。v是单词个数，v是词向量维度。 含义是中心词的词向量和上下文的词向量越相似，其概率就越大。那么想同上下文的词语，他们的词向量也就越相似（因为他们的中心词向量都和上下文词向量相似，他们之间也就相似）。

那么如何通过梯度下降优化呢，
$$\frac{\partial }{\partial v_c}J(\theta )=-\frac{1}{T}\sum _{t=1}^T\sum _{\genfrac{}{}{0ex}{}{-m\le j\le m}{j̸=0}}\frac{\partial }{\partial v_c}\log P\left(w_{t+j}|w_t;\theta \right)$$
其中：
$$\begin{array}{c}\frac{\partial }{\partial v_c}\log P(o|c)=\frac{\partial }{\partial v_c}\log \frac{\exp \left(u_o^T{v}_c\right)}{{\sum }_{w\in V}\exp \left(u_w^T{v}_c\right)}\\ =\frac{\partial }{\partial v_c}\mathrm{logexp}\left(u_o^T{v}_c\right)-\frac{\partial }{\partial v_c}\log {\sum }_{w\in V}\exp \left(u_w^T{v}_c\right)\end{array}$$
对两项分别求偏导：

第一项：$\frac{\partial }{\partial v_c}\mathrm{logexp}\left(u_o^T{v}_c\right)=u_o$

第二项复杂一些，需要用到链式法则，将log(x)看做一个整体展开：
$$\begin{gathered} \frac{\partial }{\partial v_c}\log \sum _{w\in V}\exp \left(u_w^T{v}_c\right)=\frac{1}{{\sum }_{w\in V}\exp \left(u_w^T{v}_c\right)}\ast \frac{\partial }{\partial v_c}(\sum _{x\in V}\exp \left(u_x^T{v}_c\right)) \\ =\frac{1}{{\sum }_{w\in V}\exp \left(u_w^T{v}_c\right)}\ast \sum _{x\in V}\frac{\partial }{\partial v_c}(\exp \left(u_x^T{v}_c\right)) \\ =\frac{1}{{\sum }_{w\in V}\exp \left(u_w^T{v}_c\right)}\ast \sum _{x\in V}\exp \left(u_x^T{v}_c\right)\frac{\partial }{\partial v_c}(u_x^T{v}_c) \\ =\frac{{\sum }_{x\in V}\exp \left(u_x^T{v}_c\right)u_x}{{\sum }_{w\in V}\exp \left(u_w^T{v}_c\right)} \\ =\sum _{x\in V}P(x|c)u_x \end{gathered}$$
最终：
$$\frac{\partial }{\partial v_c}\log P(o|c)=u_o-\sum _{x\in V}P(x|c)u_x$$
理解为在中心词c的情况下，预测的上下文单词和实际上下文单词向量（$u_o$）的差异，

reference

1. http://web.stanford.edu/class/cs224n/
2. https://www.bilibili.com/video/av46216519?t=4557

最后

以上就是发嗲冰棍为你收集整理的斯坦福CS224n课程笔记1-introduction and Word vectors 2019Human language and word meaningWord2vec introductionreference的全部内容，希望文章能够帮你解决斯坦福CS224n课程笔记1-introduction and Word vectors 2019Human language and word meaningWord2vec introductionreference所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。