【CodeForces500E】New Year Domino （线段树+并查集+栈）

77 阅读 0 评论 51 点赞

我是靠谱客的博主忧伤香水，最近开发中收集的这篇文章主要介绍【CodeForces500E】New Year Domino （线段树+并查集+栈），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目大意

有一排多米诺骨牌，按x坐标顺序从左到右输入，每个骨牌有他的位置p，高度l，可以花费1代价使骨牌高度+1，有q个询问，询问一个区间l，r，从l开始推倒，使[l,r]区间全部倒下的最小代价。

题解

考虑将询问排序，离线处理。
因为左边的骨牌有可能会推倒它右边的连续一段区间的骨牌，我们处理询问时应按询问左端点从右往左处理。
这里写图片描述

设当前左端点已经处理到第 l l 个骨牌。
用 $a d d$ 数组存储每个骨牌需要增加的量。
使用栈 stk s t k 存储右边还有的骨牌。

每次往左边添加一个 l l ，则后面几个被覆盖（栈里面前几个）的就需要将它们的 $a d d$ 值清零，统计它们最远的距离 far f a r ，然后使用并查集把这些被覆盖的骨牌与l合并为一个（这些被覆盖的没用了，合并相当于把它们删除），将这些点从栈里弹出，把 l l 加入栈。然后将l的长度更改为使他能达到最远距离，及 $l e n g t h_{l} := f a r - p o s_{l}$ 。将 l l 的 $a d d$ 值，更改为到 far f a r 到后一个骨牌的长度。
因为 add a d d ，需要区间清零，所以使用线段树维护 add a d d 。

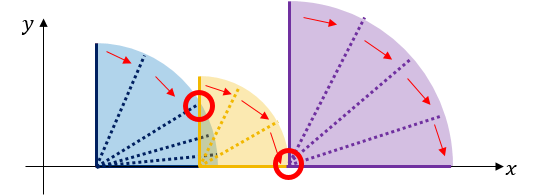
如上图例子 l l 的长度从 $8$ 更改为 10 10 ，然后用线段树将 l+1,l+2,l+3 l + 1 , l + 2 , l + 3 的 add a d d 值清零，使用并查集将这些点都和l合并为一个集合，把 add[l] a d d [ l ] 更改为 1 1 （单点修改），把 $l + 1, l + 2, l + 3$ 弹出栈，将 l l 加入栈。

询问时，l已经处理了，r更改为r所在集合的骨牌的前一个，如上图询问 $(l, l + 4)$ ，即区间查询区间 (l,l+3) ( l , l + 3 ) 的 sum s u m 。

代码

#include<cstdio>
#include<stack>
#include<algorithm>
using namespace std;
const int MAXN=200005;
int n,q;
namespace SegTree
{
int sum[MAXN*4];
bool zero[MAXN*4];
void PushUp(int id)
{
sum[id]=sum[id*2]+sum[id*2+1];
if(sum[id])zero[id]=false;
}
void PushDown(int id)
{
if(zero[id])
{
zero[id*2]=zero[id*2+1]=true;
sum[id*2]=sum[id*2+1]=0;
}
}
void Modify(int pos,int val,int L=1,int R=n,int id=1)
{
if(L==pos&&pos==R)
{
sum[id]=val;
return;
}
int mid=(L+R)/2;
if(pos<=mid)
Modify(pos,val,L,mid,id*2);
else
Modify(pos,val,mid+1,R,id*2+1);
PushUp(id);
}
void Clear(int l,int r,int L=1,int R=n,int id=1)
{
if(l>r)return;
if(l<=L&&R<=r)
{
zero[id]=true;
sum[id]=0;
return;
}
int mid=(L+R)/2;
if(l<=mid)
Clear(l,r,L,mid,id*2);
if(mid<r)
Clear(l,r,mid+1,R,id*2+1);
PushUp(id);
}
int Sum(int l,int r,int L=1,int R=n,int id=1)
{
if(l>r)return 0;
if(l<=L&&R<=r)
return sum[id];
int mid=(L+R)/2,ret=0;
PushDown(id);
if(l<=mid)
ret+=Sum(l,r,L,mid,id*2);
if(mid<r)
ret+=Sum(l,r,mid+1,R,id*2+1);
return ret;
}
}
namespace UFset
{
int fa[MAXN];
int root(int x)
{
if(fa[x]==0)
return x;
fa[x]=root(fa[x]);
return fa[x];
}
void Union(int x,int y)
{fa[y]=x;}
}
struct query
{
int l,r,id;
}que[MAXN];
bool cmp(query a,query b)
{return a.l>b.l||(a.l==b.l&&a.r<b.r);}
pair<int,int> domi[MAXN];
stack<int> stk;
int ans[MAXN];
void solve()
{
int l=n,r=n;
stk.push(n);
for(int i=1;i<=q;i++)
{
while(l>que[i].l)
{
l--;
int far=domi[l].first+domi[l].second,x;
while(!stk.empty())
{
x=stk.top();
if(domi[x].first>far)
break;
UFset::Union(l,x);
far=max(far,domi[x].first+domi[x].second);
stk.pop();
}
SegTree::Clear(l+1,x-(domi[x].first>far));
domi[l].second=far-domi[l].first;
if(far<domi[x].first)
SegTree::Modify(l,domi[x].first-far);
stk.push(l);
}
r=UFset::root(que[i].r);
r--;
if(l>r)
ans[que[i].id]=0;
else
ans[que[i].id]=SegTree::Sum(l,r);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&domi[i].first,&domi[i].second);
scanf("%d",&q);
for(int i=1;i<=q;i++)
scanf("%d%d",&que[i].l,&que[i].r),que[i].id=i;
sort(que+1,que+q+1,cmp);
solve();
for(int i=1;i<=q;i++)
printf("%dn",ans[i]);
return 0;
}