一、逻辑回归的目标
知乎用户谢澎涛是这样解释逻辑回归的目标的
设计一个分类模型,首先要给它设定一个学习目标。
在支持向量机中,这个目标是max-margin;
在adaboost中,目标是优化一个指数损失函数。
那么在logistic regression (LR)中,这个目标是什么呢?
最大化条件似然度。考虑一个二值分类问题,训练数据是一堆(特征,标记)组合,(x1,y1), (x2,y2), .... 其中x是特征向量,y是类标记(y=1表示正类,y=0表示反类)。LR首先定义一个条件概率p(y|x;w)。 p(y|x;w)表示给定特征x,类标记y的概率分布,其中w是LR的模型参数(一个超平面)。有了这个条件概率,就可以在训练数据上定义一个似然函数,然后通过最大似然来学习w。这是LR模型的基本原理。
二、为什么是sigmoid函数
那么接下来的问题是如何定义这个条件概率呢?sigmoid函数就派上用场了。
首先,看下神奇的sigmoid函数
sigmoid函数是一个良好的阈值函数,
连续,光滑严格单调关于(0,0.5)中心对称
其导数f'(x)=f(x)*[1-f(x)],可以节约计算时间
做sigmoid变换的目的是把(-inf,+inf)取值范围的信号(用x表示)映射到(0,1)范围内(用y表示):y=h(x)。
对于大多数(或者说所有)线性分类器,response value(响应值) <w,x> (w和x的内积) 代表了数据x属于正类(y=1)的confidence (置信度)。<w,x>越大,这个数据属于正类的可能性越大;<w,x>越小,属于反类的可能性越大。<w,x>在整个实数范围内取值。现在我们需要用一个函数把<w,x>从实数空间映射到条件概率p(y=1|x,w),并且希望<w,x>越大,p(y=1|x,w)越大;<w,x>越小,p(y=1|x,w)越小(等同于p(y=0|x,w)越大),而sigmoid函数恰好能实现这一功能(参见sigmoid的函数形状):首先,它的值域是(0,1),满足概率的要求;其次,它是一个单调上升函数。最终,p(y=1|x,w)=sigmoid (<w,x>).
综上,LR通过最大化类标记的条件似然度来学习一个线性分类器。为了定义这个条件概率,使用sigmoid 函数将线性分类器的响应值<w,x>映射到一个概率上。sigmoid的值域为(0,1),满足概率的要求;而且是一个单调上升函数,可将较大的<w,x>映射到较大的概率p(y=1|x,w)。sigmoid的这些良好性质恰好能满足LR的需求。
(作者:谢澎涛
链接:https://www.zhihu.com/question/35322351/answer/65308207
来源:知乎)
三、逻辑回归的目标函数与求解
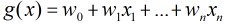
四、逻辑回归是二分类问题,但为什么叫回归
直观上看,逻辑回归是找到一个分离面,将正负样本分开。但是,逻辑回归首先将特征向量(输入值)映射到了(0,1)区间,我们希望当样例越远离分类面时,其输出值越接近0或1(正例接近1,负例接近0)。因此虽然接近的是分类问题,但是我们要训练参数使其接近我们希望的目标,中间用到了回归。
最后
以上就是孤独戒指最近收集整理的关于Logistic 回归(目标、)的全部内容,更多相关Logistic内容请搜索靠谱客的其他文章。








发表评论 取消回复