本系列翻译2003年关于LDA的一篇原始文章
隐狄利克雷分布
摘要
LDA是一种针对离散数据集合(如文本语料库)的概率生成模型。LDA是一种三层贝叶斯模型,其中集合里的每一个元素都可以看为一些潜在主题集合元素的有限次混合。反之,每一个主题可以看做是一个潜在主题概率空间集的无限混合。文本建模中,主题概率清楚的表示了一个文本。本文采用了有效的逼近推导,我们应用变分法以及用EM算法解决经验主义贝叶斯参数估计。本文最后给出了LDA与一元混合模型、PLSI模型在文本建模、文本分类和协同过滤方面的结果对比。
2.概念和术语
本文使用一些文本语言,如“词”,“文本”,“语料”。这可以帮助我们直接理解,特别是当我们引入隐变量来表示一些抽象概念,例如主题。然而,LDA模型并不仅仅适用于文本,它也有其他方面的应用,包括数据集、协同过滤相关的数据集、基于内容的图像检索以及生物信息学。在7.3节,我们将给出它在协同过滤上的实验结果。
定义以下几个概念:
- 词是离散数据的基本单元,可以定义为词库的索引{1,.....V},我们把词表示成单位向量,其中只有一维为1,其他为0。词库里的第v个词,表示成一个V -维向量w (
,
,
)
- 文本是由N个词组成的序列
,其中
为序列的第n个词。
- 语料库由M个文本组成
我们希望找到一个概率模型,使得对给定的语料库,其中的每个文本以高概率出现,并且对于其他相似文本也以高概率出现。
3.隐狄利克雷分布
LDA是关于语料库的生成概率模型,其基本思想是:文本可以表示成潜在主题的随机混合,而每个主题由主题中词的分布决定。
LDA假设语料库![]() 中每篇文章
中每篇文章![]() 的生成过程为:
的生成过程为:
1. 选择![]()


2. 选择![]()


3. 对于文本中的任一词
![]() :
:

(a) 选择一个主题![]()


(b) 在主题![]() 上的一个多项式条件概率分布
上的一个多项式条件概率分布![]() 中选择一个词
中选择一个词![]()


基本模型中,我们有以下几点假设:
1. 狄利克雷分布的维数k(主题变量z的个数)已知且为常量
2. 词的概率分布的参数为一个
![]() 的矩阵
的矩阵
![]() ,其中
,其中
![]() ,我们暂且把它看成一个要估计的固定常量
,我们暂且把它看成一个要估计的固定常量



3. 泊松假设并不是唯一的,可以根据实际文本长度的需要来决定
4. N是独立的辅助变量,我们可以把它看成一个常量
k维随机变量![]() ,可以把它限制在k-1维单纯形上(因为
,可以把它限制在k-1维单纯形上(因为
![]() ),且有如下概率密度:
),且有如下概率密度:


其中![]()
 为k维正实数向量,
为k维正实数向量,![]()
 是伽马函数。狄利克雷分布是一种很实用的分布---它属于指数分布族;有有限维的充分统计量;是多项式分布的共轭分布。这些性质将有助于第五节LDA算法的推导和参数估计。
是伽马函数。狄利克雷分布是一种很实用的分布---它属于指数分布族;有有限维的充分统计量;是多项式分布的共轭分布。这些性质将有助于第五节LDA算法的推导和参数估计。
 为k维正实数向量,
为k维正实数向量, 是伽马函数。狄利克雷分布是一种很实用的分布---它属于指数分布族;有有限维的充分统计量;是多项式分布的共轭分布。这些性质将有助于第五节LDA算法的推导和参数估计。
是伽马函数。狄利克雷分布是一种很实用的分布---它属于指数分布族;有有限维的充分统计量;是多项式分布的共轭分布。这些性质将有助于第五节LDA算法的推导和参数估计。
考虑参数![]()
 和
和![]()
 ,则混合主题
,则混合主题
![]() ,k个主题集
,k个主题集
![]() ,N个词集
,N个词集
![]() 的联合概率分布为:
的联合概率分布为:
 和
和 ,则混合主题
,则混合主题


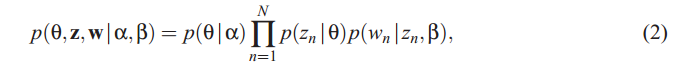
其中
![]() 是p(
是p(![]()
![]()
 |
| )的简化。因此一个文本的边缘分布为:
)的简化。因此一个文本的边缘分布为:

 |
| )的简化。因此一个文本的边缘分布为:
)的简化。因此一个文本的边缘分布为:
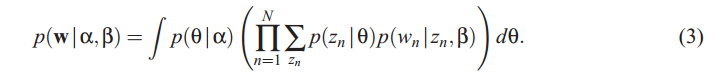
而一个语料库的生成概率为所有文本概率的乘积:

LDA模型可以表示成如图1所示的概率图模型。

如图所示,LDA是一个三层模型。![]()
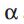 和
和![]()
 为语料层参数,在形成语料库的过程中被取样一次。变量
为语料层参数,在形成语料库的过程中被取样一次。变量
![]() 为文本层变量,在每个文本中取样一次。变量
为文本层变量,在每个文本中取样一次。变量![]()
 和
和![]()
 为词层变量,在文本的每个词中取样一次。
为词层变量,在文本的每个词中取样一次。
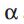 和
和 为语料层参数,在形成语料库的过程中被取样一次。变量
为语料层参数,在形成语料库的过程中被取样一次。变量
 和
和 为词层变量,在文本的每个词中取样一次。
为词层变量,在文本的每个词中取样一次。
LDA与简单的狄利克雷-多项式分布聚类模型有很大区别。典型的聚类模型为二层模型,其中在语料层,狄利克雷分布被取样一次,而在语料的每个文本中取样一次多项式聚类变量,文本的每个词取决于在这些聚类变量上的条件分布,正如其他聚类模型,文本只跟一个主题相关。LDA是三层模型,文本可以跟多个主题相关。
贝叶斯统计模型的结构跟图1类似,我们把它叫着层次模型![]()
 ,准确来讲应该为条件独立的层次模型
,准确来讲应该为条件独立的层次模型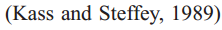 ,这种模型也可称为参数化经验主义的贝叶斯模型,它不仅是一种特殊的模型结构,也可用于参数估计。事实上,在第5节中,我们将采用经验主义的贝叶斯方法估计参数,比如LDA的
,这种模型也可称为参数化经验主义的贝叶斯模型,它不仅是一种特殊的模型结构,也可用于参数估计。事实上,在第5节中,我们将采用经验主义的贝叶斯方法估计参数,比如LDA的![]() 和
和![]() 参数,但我们也会充分利用贝叶斯定理。
参数,但我们也会充分利用贝叶斯定理。
 ,准确来讲应该为条件独立的层次模型
,准确来讲应该为条件独立的层次模型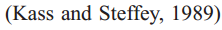 ,这种模型也可称为参数化经验主义的贝叶斯模型,它不仅是一种特殊的模型结构,也可用于参数估计。事实上,在第5节中,我们将采用经验主义的贝叶斯方法估计参数,比如LDA的
,这种模型也可称为参数化经验主义的贝叶斯模型,它不仅是一种特殊的模型结构,也可用于参数估计。事实上,在第5节中,我们将采用经验主义的贝叶斯方法估计参数,比如LDA的
3.1 LDA和可交换性
随机变量有穷集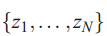
![]() 是可交换的,如果它们的联合分布对置换集不变。即,
是可交换的,如果它们的联合分布对置换集不变。即,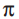 若
若![]() 为整数集1到N的一个置换,则
为整数集1到N的一个置换,则
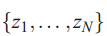
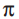 若
若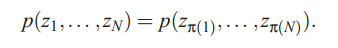
随机变量无穷集是无穷可交换的,如果它的任一有限子序列是可交换的。
 的表示法理论认为随机变量无穷可交换集的联合概率分布,可以看为随机参数服从某种分布,而相应的随机变量是条件独立同分布的。
的表示法理论认为随机变量无穷可交换集的联合概率分布,可以看为随机参数服从某种分布,而相应的随机变量是条件独立同分布的。
在LDA中,我们假设词由主题生成,且某个文本中的主题是无穷可交换的,由![]()
 理论可知,词和主题的概率分布为:
理论可知,词和主题的概率分布为:
 理论可知,词和主题的概率分布为:
理论可知,词和主题的概率分布为:

其中![]()
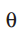 是产生主题的随机参数,通过边缘化主题变量,且
是产生主题的随机参数,通过边缘化主题变量,且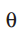
![]() 服从狄利克雷分布,可得文本的LDA分布如方程(3)所示。
服从狄利克雷分布,可得文本的LDA分布如方程(3)所示。
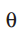 是产生主题的随机参数,通过边缘化主题变量,且
是产生主题的随机参数,通过边缘化主题变量,且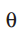
3.2 连续一元混合
图1所示的LDA模型一般比经常用于分类层次贝叶斯语言的二层模型更精细,通过对隐变量主题z边缘化,我们可以把LDA看成二层模型。
词的概率分布![]()
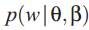 :
:
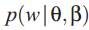 :
:
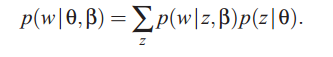
注意这是一个取决于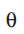
![]() 的随机量。
的随机量。
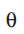
现在我们定义文本![]() 的生成过程:
的生成过程:
1. 选择![]()


2. 对文本中的任一词![]()
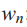 :
:
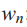 :
:
(a) 从概率分布![]() 中
中 选择
选择![]()
 选择
选择
因此一个文本的边缘分布为连续的混合分布:
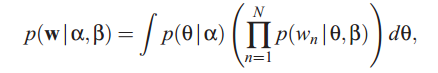
其中![]()
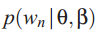 是混合的成分,
是混合的成分,
![]() 是混合的权值。
是混合的权值。
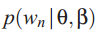 是混合的成分,
是混合的成分,
图2解释了上述LDA的观点。注意,这个只有![]()
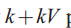 个参数的
个参数的![]()
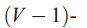 单纯形产生了一个有趣的多峰结构。
单纯形产生了一个有趣的多峰结构。
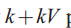 个参数的
个参数的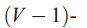 单纯形产生了一个有趣的多峰结构。
单纯形产生了一个有趣的多峰结构。
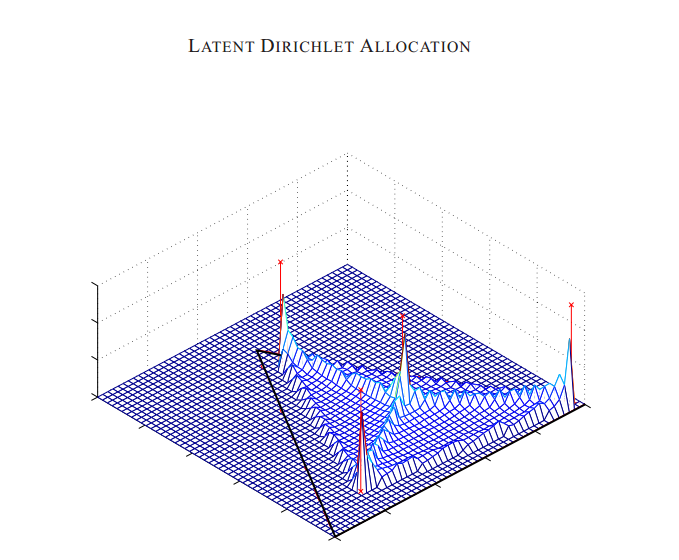
图2:三个词,四个主题的LDA的一元分布
![]() 的例子。
的例子。

在![]() 平面上的三角形区域表示三个词的所有可能的多项式分布。三角形的每个顶点对应于词之间的确定性分布;三角形的边的中点代表给边上二个词的概率都为0.5;而三角形的中心代表这三个词的一元分布;四个标记为x的点为四个主题下的多项式分布
平面上的三角形区域表示三个词的所有可能的多项式分布。三角形的每个顶点对应于词之间的确定性分布;三角形的边的中点代表给边上二个词的概率都为0.5;而三角形的中心代表这三个词的一元分布;四个标记为x的点为四个主题下的多项式分布![]()
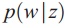 ;在单纯形顶端的表面是关于LDA的
;在单纯形顶端的表面是关于LDA的![]()
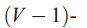 单纯形分布(词的多项式分布)的一个例子
单纯形分布(词的多项式分布)的一个例子
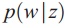 ;在单纯形顶端的表面是关于LDA的
;在单纯形顶端的表面是关于LDA的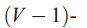 单纯形分布(词的多项式分布)的一个例子
单纯形分布(词的多项式分布)的一个例子
最后
以上就是缓慢红牛最近收集整理的关于LDA--隐狄利克雷分布(摘要以及2,3节)的全部内容,更多相关LDA--隐狄利克雷分布(摘要以及2内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。












发表评论 取消回复