概述
时间序列的反向传播算法
BPTT ： Back-Propagation Through Time
∂
L
∂
U
=
∑
t
∂
L
t
∂
U
frac{partial L}{partial U} = sum_tfrac{partial L_t}{partial U}
∂U∂L=∑t∂U∂Lt
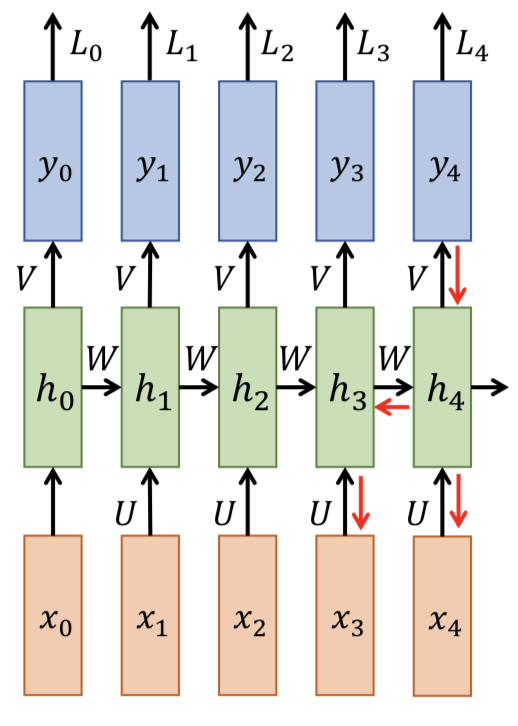
例如t=4 时，
∂ L 4 ∂ U = ∂ L 4 ∂ y 4 ∂ y 4 ∂ h 4 ∂ h 4 ∂ U frac{partial L_4}{partial U} =frac{partial L_4}{partial y_4} frac{partial y_4}{partial h_4} frac{partial h_4}{partial U} ∂U∂L4=∂y4∂L4∂h4∂y4∂U∂h4
where h 4 = t a n h ( W h 3 + U x 4 ) h_4 = tanh(Wh_3 + Ux_4) h4=tanh(Wh3+Ux4)
注意到 h3也依赖U
∂
L
t
∂
U
=
∑
s
=
0
t
∂
L
t
∂
y
t
∂
y
t
∂
h
t
∂
h
t
∂
h
s
∂
h
s
∂
U
frac{partial L_t}{partial U} = sum_{s=0}^tfrac{partial L_t}{partial y_t} frac{partial y_t}{partial h_t} frac{partial h_t}{partial h_s}frac{partial h_s}{partial U}
∂U∂Lt=∑s=0t∂yt∂Lt∂ht∂yt∂hs∂ht∂U∂hs
参数共享是双刃剑，网络预测时具有平稳性，但是梯度计算的时候会有依赖。
随着t和s的距离越来越大，梯度传播的计算，长时序的依赖不足。
∂
h
t
∂
h
s
=
∂
h
t
∂
h
t
−
1
∂
h
t
−
1
∂
h
t
−
2
.
.
.
∂
h
s
+
1
∂
h
s
frac{partial h_t}{partial h_s} = frac{partial h_t}{partial h_{t-1}} frac{partial h_{t-1}}{partial h_{t-2}} ... frac{partial h_{s+1}}{partial h_{s}}
∂hs∂ht=∂ht−1∂ht∂ht−2∂ht−1...∂hs∂hs+1
Truncated BPTT
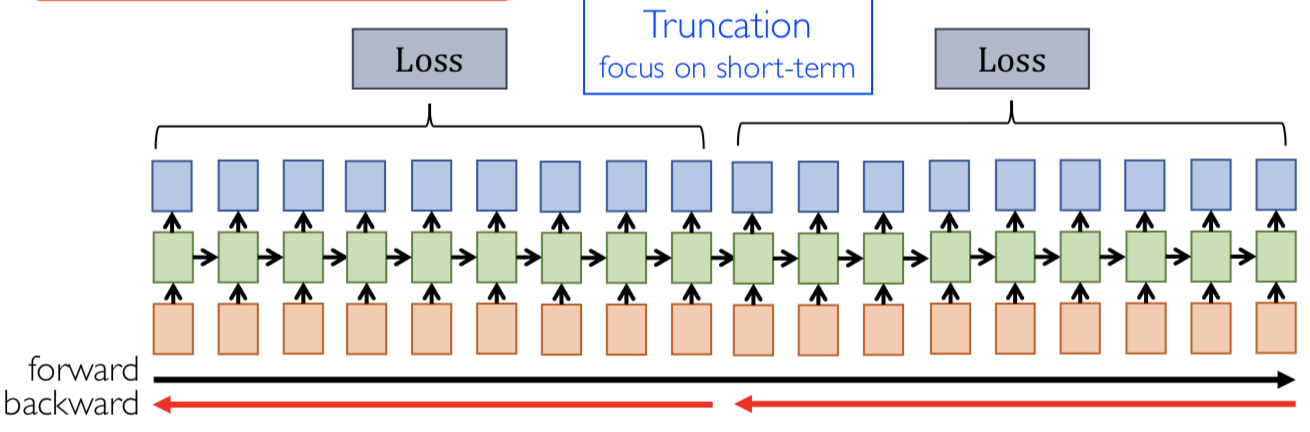
BPTT 只在子序列的内部去做反向传播，只关心内部的计算。在实际的计算中，很少有人用 full BPTT，一般是使用 Truncated BPTT。
最后
以上就是成就钢笔为你收集整理的时间序列的反向传播算法（BPTT）的全部内容，希望文章能够帮你解决时间序列的反向传播算法（BPTT）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复