POJ 1177 picture(扫描线入门)

扫描线

求n个矩形面积并

1. 将每个矩形拆成垂直x轴的两条边,一条为入边,一条为出边
2. 我们假想有一条无限长的垂直x轴的扫描线从最左边的边开始向右进行扫描
3. 每次遇到一条边,他和前面一条边就能构成一个规则的矩形,答案增加两条边x的距离*当前扫描线的长度,若当前边为入边,就扩充扫描线的长度,若为出边,就在扫描线中去掉这条线的长度.
4. 扫描到最后一条边,得出答案

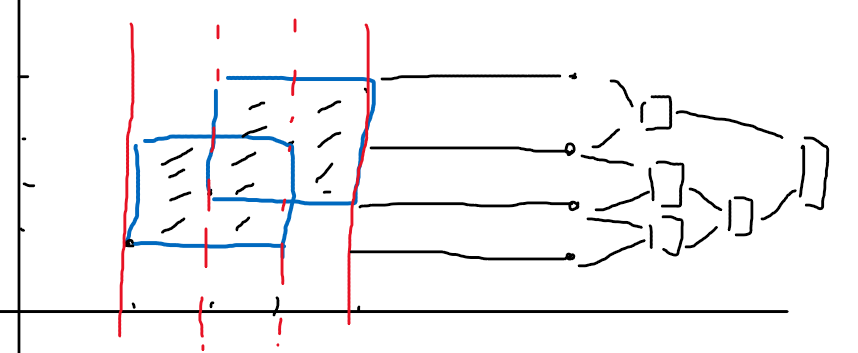
使用线段树来完成线段的操作,右边是建立的线段树的节点,具体看注释

#include<bits/stdc++.h>
#define ll long long
#define ls(i) i<<1
#define rs(i) i<<1|1
using namespace std;
const int N = 2e5+10;
struct node{
// 节点
int l,r;
// l,r为当前节点的左右值域,不再代表区间下标
int len;
int cover;
}sgt[N<<3]; // 8倍空间
int v[N];
// 横边的y坐标
struct L{
int x,y1,y2;
// 一条垂直x轴的线段 y1<y2
int state;
// 入边/出边
bool operator<(L oth)const{return x < oth.x;}// x从小到大排序
}line[N];
// 更新长度
void pushup(int rt){
if(sgt[rt].cover)
sgt[rt].len = sgt[rt].r - sgt[rt].l;
// 如果当前区间被覆盖了,长度就是右端点-左端点
else sgt[rt].len
= sgt[ls(rt)].len + sgt[rs(rt)].len;
// 否则就是左儿子的长度+右儿子的长度
}
void build(int l,int r,int rt=1){
sgt[rt].l = v[l];
sgt[rt].r = v[r]; // 值赋给左右端点
if(l+1>=r)
return ;
// 叶子节点长度为2
int mid = (l+r)>>1;
build(l,mid,ls(rt));
build(mid,r,rs(rt));
// 区间是连续的 mid 而不是 mid+1
}
// 加入下一条线段
yl,yr代表y轴上一段区间
op代表是入边还是出边
void modify(int yl,int yr,int op,int rt=1){
int l = sgt[rt].l, r = sgt[rt].r;
// 左右区间
if(yl<=l && yr>=r){ // 被完全覆盖
sgt[rt].cover += op;
// 修改当前节点被覆盖的线段个数
pushup(rt);
// 更新长度
return ;
}
if(yl<sgt[ls(rt)].r)
modify(yl,yr,op,ls(rt));
// 落在左儿子
if(yr>sgt[rs(rt)].l)
modify(yl,yr,op,rs(rt));
// 落在右儿子
// 注意: 我们对y的每个可能取值都建了节点,所以最终一定会有节点被yl,yr,完全覆盖
pushup(rt);
}
int main(){
int n,x1,x2,y1,y2;
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
v[i] = y1;
v[i+n] = y2;
// 加点
line[i]=(L){x1,y1,y2,1};
// 加边
line[i+n]=(L){x2,y1,y2,-1};
}
sort(v+1,v+1+n*2);
// 点边排序
sort(line+1,line+1+n*2);
build(1,n*2,1);
// 建树 n个矩形,2*n个线段
unsigned ll ans = 0;
for(int i=1;i<=n*2;++i){
// 向右移动
ans += sgt[1].len *1LL* (line[i].x - line[i-1].x);
// 更新答案
modify(line[i].y1,line[i].y2,line[i].state,1);
// 加边
// cout << sgt[1].len << endl;
}
printf("%llun",ans);
}

luogu P5490
大佬视频

POJ 1177 Picture

• 题意: 求矩形并后周长

#include<bits/stdc++.h>
#define ll long long
#define ls(i) i<<1
#define rs(i) i<<1|1
using namespace std;
const int N = 2e5+10;
struct node{
int l,r;
// 左右下标
int len;
// 区间长度
int cover;
// 被覆盖多少次
int num;
// 区间上有多少条线段
int lf,rf;
// 左右区间值域
bool lb,rb;
// 左右孩子是否被覆盖
}sgt[N<<3];
struct L{
int x,y1,y2;
// 垂直x轴的线段
int state;
// 入边/出边
bool operator<(L oth)const{
if(x==oth.x)
return state > oth.state;
return x < oth.x;
}
}line[N];
int y[N];
void pushup(int rt){
if(sgt[rt].cover){
// 被完全覆盖
sgt[rt].len = sgt[rt].rf - sgt[rt].lf;
sgt[rt].num = 1;
sgt[rt].lb = sgt[rt].rb = 1;
}
else if(sgt[rt].l+1==sgt[rt].r){
// 节点为叶子,且没被覆盖
sgt[rt].rb = sgt[rt].lb = 0;
sgt[rt].len = sgt[rt].num = 0;
}else{
// 用左右儿子更新自己
sgt[rt].rb = sgt[rs(rt)].rb;
sgt[rt].lb = sgt[ls(rt)].lb;
sgt[rt].len = sgt[ls(rt)].len + sgt[rs(rt)].len;
sgt[rt].num = sgt[ls(rt)].num + sgt[rs(rt)].num ;
if(sgt[ls(rt)].rb && sgt[rs(rt)].lb) sgt[rt].num--;
// 左儿子右边被覆盖,右儿子左边被覆盖,是被同一条线段覆盖,个数--
}
}
// 建树
void build(int l,int r,int rt=1){
sgt[rt].l = l;
sgt[rt].r = r;
sgt[rt].num = 0;
sgt[rt].lf = y[l];
sgt[rt].rf = y[r];
if(l+1>=r)
return ;
int mid = (l+r)>>1;
build(l,mid,ls(rt));
build(mid,r,rs(rt));
}
// 加边
void modify(int yl,int yr,int op,int rt=1){
int lf = sgt[rt].lf, rf = sgt[rt].rf;
if(yl<=lf && yr>=rf){
// 被覆盖
sgt[rt].cover += op;
pushup(rt);
return ;
}
if(yl<sgt[ls(rt)].rf)
modify(yl,yr,op,ls(rt));
// 落入左儿子
if(yr>sgt[rs(rt)].lf)
modify(yl,yr,op,rs(rt));
// 落入右儿子
pushup(rt);
}
int main(){
int n,x1,x2,y1,y2;
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
y[i] = y1;
y[i+n] = y2;
line[i]=(L){x1,y1,y2,1};
line[i+n]=(L){x2,y1,y2,-1};
}
sort(y+1,y+1+n*2);
sort(line+1,line+1+n*2);
int m = unique(y+1,y+1+n*2)-y-1;// 离散化 获得y值个数
build(1,m,1);
// 根据y的个数建树
int ans = 0,last = 0,lines = 0;
for(int i=1;i<=n*2;++i){
// 扫描
modify(line[i].y1,line[i].y2,line[i].state,1);
// 加入当前边
ans += lines *2LL* (line[i].x - line[i-1].x);
// 算平行于x轴的周长,每条线段贡献两次
ans += abs(sgt[1].len - last);
// 计算垂直x轴的长度,根节点存的是当前扫描线的长度,与上一次做差,即为变化的长度(变长为入边,变少为出边)
last = sgt[1].len;
// 上一次的长度
lines = sgt[1].num; //
上一次线段个数
}
printf("%dn",ans);
}

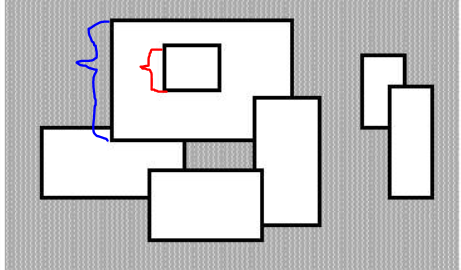
一开始不明白这种情况,在更新红线时,因为蓝线已经把大区间完全覆盖了,所以虽然红线会更新大区间的子区间,但子区间的信息并不会传递到大区间上