【HDU 1828】Picture 线段树扫描线

60 阅读 0 评论 40 点赞

我是靠谱客的博主洁净滑板，最近开发中收集的这篇文章主要介绍【HDU 1828】Picture 线段树扫描线，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Picture

Time Limit: 6000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 6289 Accepted Submission(s): 2935

Problem Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

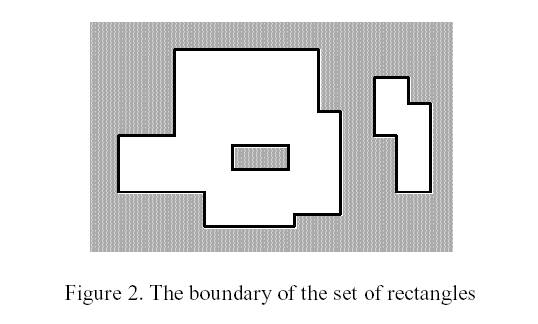
The vertices of all rectangles have integer coordinates.

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Please process to the end of file.

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

Sample Input

7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16

Sample Output

228

题目大意：给出若干个矩形，求这些矩形交叠成的图形的周长。

（如果之前没有了解过扫描线，请移步：https://blog.csdn.net/hxtscjk/article/details/81051412，是一道扫描线求覆盖面积的题，我个人觉得要比求周长容易理解一些。）

首先我们可以把周长分成两类，一类是横线，一类是竖线。

横线的求法比较简单，从下向上扫描，一边扫描一边将图形向下投影，然后计算加入某条线之前和之后的投影长度差，得出的就是加入了这条线后整个图形增加的周长长度。因为既然投影长度改变了，那么肯定是扫描到了边缘位置，边缘位置就是周长要计算的地方了。

至于竖线的求法，由于它也涉及到了图形相互覆盖，插入又移除的问题，也需要利用线段树来计算。要计算的竖线所在的位置在投影上也有体现，即：投影上的长度是由N条线段组成，就有2*N条竖线需要计算。所以就可以把问题转化成投影中有几条线段了。这样在树中再定义一个计数的变量，和线段在区间内覆盖的左右端点两个变量，在pushup操作中将它们的计算涵盖进入，就能得出最后的答案了。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
struct node
{
int l,r,pos,s;
}k[10010];
struct node1
{
int left,right,s;//对应节点的左右端点以及上下边的标记
int sumd;//图中横线的总长度
int sumv;//图中被覆盖的部分的块数
int lmax,rmax;//图中被覆盖部分的最左和最右端点
}tree[80010];
int x[10010];
int qwe(node x,node y)
{
return x.pos<y.pos;
}
void build_tree(int root,int left,int right)
{
tree[root].left=left;
tree[root].right=right;
tree[root].s=0;
tree[root].sumd=0;
tree[root].sumv=0;
tree[root].lmax=0;
tree[root].rmax=0;
if(left==right)return ;
int mid=(left+right)/2;
build_tree(root*2,left,mid);
build_tree(root*2+1,mid+1,right);
}
void push_up(int root)
{
if(tree[root].s)
{
tree[root].lmax=tree[root].left;
tree[root].rmax=tree[root].right;
tree[root].sumv=1;
tree[root].sumd=x[tree[root].right+1]-x[tree[root].left];
}
else if(tree[root].left==tree[root].right)
{
tree[root].lmax=0;
tree[root].rmax=0;
tree[root].sumv=0;
tree[root].sumd=0;
}
else
{
tree[root].lmax=tree[root*2].lmax;
tree[root].rmax=tree[root*2+1].rmax;
tree[root].sumd=tree[root*2].sumd+tree[root*2+1].sumd;
if(tree[root*2].rmax==tree[root*2+1].lmax-1)//如果左右端点区间相连
tree[root].sumv=tree[root*2].sumv+tree[root*2+1].sumv-1;
else//不相连
tree[root].sumv=tree[root*2].sumv+tree[root*2+1].sumv;
}
}
void update_tree(int root,int left,int right,int s)
{
if(tree[root].left==left&&tree[root].right==right)
{
tree[root].s+=s;
push_up(root);
return ;
}
int mid=(tree[root].left+tree[root].right)/2;
if(right<=mid)update_tree(root*2,left,right,s);
else if(left>=mid+1)update_tree(root*2+1,left,right,s);
else
{
update_tree(root*2,left,mid,s);
update_tree(root*2+1,mid+1,right,s);
}
push_up(root);
}
int main()
{
int n,x1,y1,x2,y2;
while(~scanf("%d",&n))
{
int cntk=1;int cntx=1;
for(int i=0;i<n;i++)
{
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
k[cntk].l=x1;
k[cntk].r=x2;
k[cntk].s=1;
k[cntk++].pos=y1;
x[cntx++]=x1;
k[cntk].l=x1;
k[cntk].r=x2;
k[cntk].s=-1;
k[cntk++].pos=y2;
x[cntx++]=x2;
}
sort(k+1,k+cntk,qwe);
sort(x+1,x+cntx);
int num=2;//去重
for(int i=2;i<cntx;i++)
{
if(x[i]!=x[i-1])x[num++]=x[i];
}
cntx=num;
build_tree(1,1,cntk-2);
int sum=0;int xx=0;
for(int i=1;i<cntk;i++)
{
int l=lower_bound(x+1,x+cntx,k[i].l)-x;
int r=lower_bound(x+1,x+cntx,k[i].r)-x-1;
update_tree(1,l,r,k[i].s);
sum+=abs(tree[1].sumd-xx);//这次和上次投影的长度差
xx=tree[1].sumd;
sum+=(tree[1].sumv*(k[i+1].pos-k[i].pos)*2);
}//再加上覆盖的段数*高度*左右2条线
printf("%dn",sum);
}
}