一、概述

  近日，随着GPT-3模型的新鲜出炉，NLP领域似乎正朝着“烧钱+烧数据”的方向一去不返。从18年的BERT，到19年XLNet，再到如今的GPT-3，烧钱模式愈演愈烈，NLP似乎已经不适合穷人研究了，调参侠的生存空间被严重挤压。尽管如此，在如今开口不提BERT就不好意思说自己是NLPer的时代，我们还是很有必要对这些模型进行深入的了解的。本文主要是借着课程需要的契机，非常非常非常非常详细的介绍XLNet模型。至于XLNet的源码，看情况考虑是否阅读。

二、背景知识

​   XLNet需要的背景知识非常多，建议不懂的需要补一下。本文也会介绍一些，也会列出一些资料供大家参考。

BERT相关：

​   BERT论文、《attention is all you need》

​    BERT博客（强烈建议）： https://blog.csdn.net/cpluss/article/details/88418176

XLNet相关：

​   XLNet论文、Transformer-xl论文（Transformer-xl并非XLNet的主要思想，但对XLNet非常重要）

1、自编码模型和自回归模型

​   自编码模型定义：给定输入x，经过编码层编码为y，再经过解码层解码为z，要求z和x要尽可能的相同。

​ 图示：

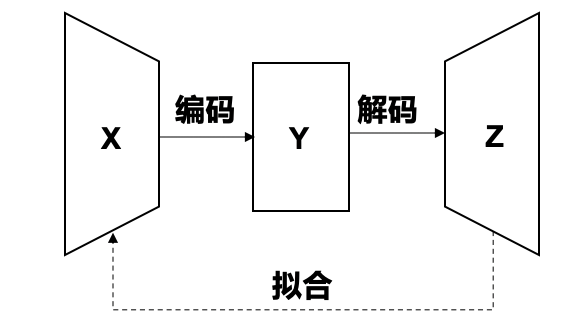
​   解释：从图中可以看出，自编码模型要求输出z尽可能的和输入x相同，二者越相似，说明中间层结果Y就包含了越多的x的信息。那么这种模型有什么作用呢？最显而易见的作用就是降维。假设x是需要降维的数据，y的维度小于x，那么y就可以很好的代表x，因为从y可以解码出z，z又是x的近似。（我们所熟悉的PCA降维，其实就是一种线性自编码器，考虑PCA的“最小化重建误差”，是不是和自编码模型的原理相同呢？）

​   自回归模型定义：时间序列模型，某一时刻t的输出和前面所有t-1个时刻相关。

​ 图示：

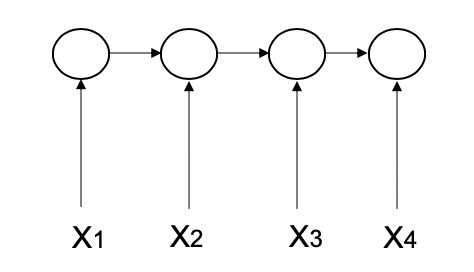
​   解释：从图中可以看出，t=3时刻的输出和t=2、t=1时刻都相关。自回归模型的应用也很多，比如我们熟悉的seq2seq模型的解码阶段，ELMO模型等。

2、BERT模型

​   为什么要介绍BERT呢？XLNet可以说是BERT的改进版，通篇都是根据BERT的缺点进行改进的，所以有必要简单介绍一下BERT，另外，详细的介绍可以参考：https://blog.csdn.net/cpluss/article/details/88418176。

​   BERT最重要的部分就是Transformer了，Transformer最重要的则是self-attention。但是，在这里并不是我们的重点，我们只是简单的给出self-attention图示：

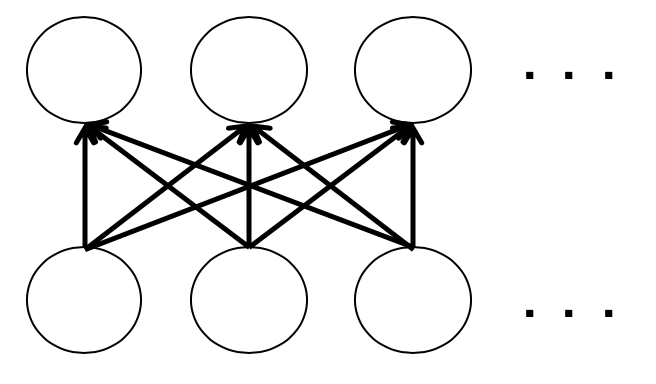
​   解释：这应该是简单的不能再简单的自注意力机制图示了，但是我觉得完全可以说明问题。每一层的输出都和上一层所有的输入相关（这就保证了每一个节点都可以获得上下文的信息）。为什么叫自注意力机制呢？因为query=key=value，什么都是自己，当然叫自注意力了。

​   当然，Transformer的架构显然没有那么简单，但是对于XLNet，了解到这里就够了，详细的可以参考上面列出的博客。

​   另一个重要的点，也是XLNet的突破口，则是Masked Language Model，掩码模型。简单来说，就是BERT模型随机掩盖输入x的15%的单词，然后BERT的目标就是预测这些被掩盖的单词。注意，这是一个预训练任务。我们知道，预训练+微调模式的模型，首先需要预训练，然后根据具体的任务进行微调，这种二阶段模式很有可能成为以后的主流。

​   下面给出第一个结论：BERT模型就是自编码模型，属于降噪自编码模型。

​   什么又是降噪自编码模型呢？就是我们的输入x是有噪声的，然后利用这个有噪声的x作为输入，重构x。用图可以简单的表示为下图：

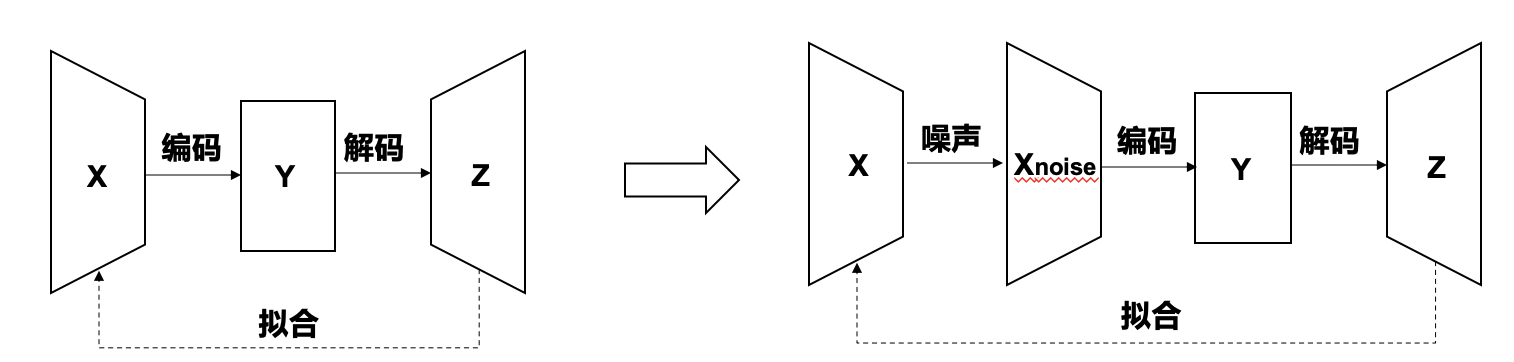
​   Masked LM通过对x进行随机的掩盖单词，生成带有噪声的数据x-noise，然后送进自编码器（也就是BERT），经过编码和解码得到再z，再用z去拟合x（其实是利用解码的输出预测被mask的单词，相当于去还原x）。

3、公式表达

​   公式总是枯燥的，但又是充满信息的。从上面的图示中，很难看出BERT还有什么缺点，因此只有从公示入手。
$$\begin{gathered} 自编码模型：log{P}_{\theta }(x|\tilde{x})\approx log\prod _{t=1}^T{m}_t{p}_{\theta }(x|\tilde{x})=\sum _{t=1}^T{m}_{t}log\frac{exp(H_{\theta }(\tilde{x}{)}_t^{T}e(x_t))}{{\sum }_{x^{,}}exp(H_{\theta }(\tilde{x}{)}_t^{T}e(x^{,}))} \\ x:原始输入\tilde{x}:带有噪声的输入（mask标志）m_t:1代表t位置的词语被mask，0代表没有被mask \\ {H}_{\theta }(\tilde{x}{)}_t^T:t位置transformer的隐层状态输出，T代表转置e(x_t):t位置的embedding表示 \end{gathered}$$
​   公式分析：
$$\begin{gathered} 第一部分用\tilde{x}预测x正是降噪自编码器的定义。重点在于第二部分以及第一部分和第二部分之间为什么要用约等号。 \\ 对于第二部分，m_t=1时(t位置被mask时)，t位置才参与运算，也就是说，连乘的只是被预测单词的概率， \\ 其它没有被mask的单词并不被预测。第三部分则是一个softmax，用t位置的隐状态乘以x_t的embedding。 \\ 注意，H_{\theta }(\tilde{x}{)}_t代表t位置的隐状态，包含t位置的上下文信息（参考transformer机制的含义） \\ 那么为什么用约等号呢？我们注意到在预测一个mask时，另一个mask并没有起作用！（参考图5） \end{gathered}$$

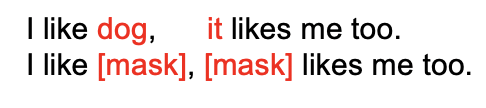
​   图示分析：图五仍然是用来解释为什么用约等号的。原始句子是上句，输入的带噪声的句子是下句。**我们在预测第一个mask时，我们是不知道第二个mask的信息的；同理，我们在预测第二个mask的时候，也是不知道第一个mask的信息的。**以上图为例，预测dog时，知道第二个mask是it很有帮助（至少确定第一个mask不是人）；预测it时，知道第一个mask是dog更有用，这样可以直接排除he/she等。但是遗憾的是，我们不知道。（有人肯定要问，第一个mask处的hidden不是包含上下文的信息吗？那么它应该有第二个mask的信息啊。这句话的前半句话是对的，既是第一个mask处的hidden确实包含上下文的信息，但他的下文信息包含的是mask，而不是it！因为输入并没有it，transformer再强大，也不能从中抽取到it的信息吧，所以第一个mask看不到it。不知道这样说能不能理解）

​   以上是BERT的词语独立性假设，也是XLNet的切入口。另一个缺点就很简单了，姑且翻译成预训练-微调差异吧。什么意思呢？就是预训练时会出现mask标志，微调时具体的任务是不会出现mask的。所以说这个mask就是个噪声。

​   总结一下BERT的优缺点，就可以发现全是mask lm造成的，真是万恶之源！

优点：能看到上下文信息
缺点1:词语独立性假设
缺点2:预训练-微调差异

​   讲完了以BERT为代表的自编码模型的优缺点，就可以分析自回归模型的优缺点了。“巧合的是”，二者的优缺点是互换的：自回归模型没有引入mask，所以BERT的缺点他没有。但是注意，自回归模型是逐个预测单词，预测一个单词时，需要看到前面所有的单词，但是并没有去看后面的单词，因此自回归模型是一个单向模型，无法看到下文信息，这也是自回归模型目前效果比较差的原因。

​   既然写出了自编码模型的公式表达，就把自回归模型的表达也补充一下：
$$自回归模型：log{P}_{\theta }(x)=log\prod _{t=1}^{T}p(x_t|x_{<t})=\sum _{t=1}^{T}log\frac{exp(h_{\theta }(x_{1:t-1}{)}^{T}e(x_t))}{{\sum }_{x^{,}}exp(H_{\theta }(x_{1:t-1}{)}^{T}e(x^{,}))}$$

三、XLNet模型核心思想

1、why

​   讲了那么多，其实也只是背景知识，但这些背景知识很重要。他告诉了我们要做什么，为什么要这么做，为我们指明了方向。那么为什么要提出XLNet？当然是因为BERT优缺点，自回归有优点了。优缺点上面说的已经很明白了，XLNet的使命就是组合自回归模型和自编码模型的优点。想想一个既能看到上下文，又没有独立性假设和预训练微调差异的模型，是有多完美！目标有了，下面的就是如何实现了。其实到此为止，才刚刚进入正式环节，但是我觉得知道动机和目标很重要，所以花了一点时间去总结。

2、how

​   XLNet的基本盘是自回归模型，不引入mask标志，那么很显然就没有BERT的那两个缺点了，**现在问题是如何让自回归模型既能看到上文信息，又能看到下文信息。**XLNet最最最最最最最最核心的思想就在于此。

Permutation Language Model

​   中文名叫排列语言模型。这个模型就是为了解决自回归模型只能看到上文或只能看到下文的缺点。下面将分成若干步骤来介绍这个模型。

1、什么是排列语言模型

​   排列，就是给定一个系列数据，然后随机排列成一个新的序列。例如：
$$[1,2,3]的排列:[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]$$
​   所谓排列语言模型，就是不针对正常的顺序建模，而是针对正常顺序的某一个排列建模。举个例子就很好明白了：
$$\begin{gathered} 输入：x_1{x}_2{x}_3{x}_4 \\ 正常[1,2,3,4]建模：log\prod _{t=1}^{T}p(x_t|x_{<t})=logp(x_1)p(x_2|x_1)p(x_3|x_2{x}_1)p(x_4|x_3{x}_2{x}_1) \\ 排列[3,1,4,2]建模:logp(x_3)p(x_1|x_3)p(x_4|x_1{x}_3)p(x_2|x_4{x}_1{x}_3) \\ 排列[2,4,3,1]建模:logp(x_2)p(x_4|x_2)p(x_3|x_4{x}_2)p(x_1|x_3{x}_4{x}_2) \end{gathered}$$
​   这就是排列语言模型。注意，一个序列长度为10的输入，他的全排列就有10！个，因此显然不能为所有的排列建模，而是随机选取一个进行建模。

​   因此，排列模型有什么优点和缺点呢？他又解决了什么问题呢？

2、排列语言模型的优点

​   我们知道，排列语言模型是为了解决自回归模型不能看到上下文而提出的，那么很显然，排列语言模型的优点就是能看到上下文。排列语言模型是如何做到这一点的呢？考虑一个排列[2,4,3,1]，我们在计算3的概率的时候，是不是既看到了2，又看到了4。因此是能看到上下文。现在有个点需要明确一下：并不是所有的排列都能看到上下文。例如，上例中的4只能看到2，那么这个排列预测4时，就只能看到上文，而且是部分上文。

​   可能看到这里还比较模糊，那就上图举例。

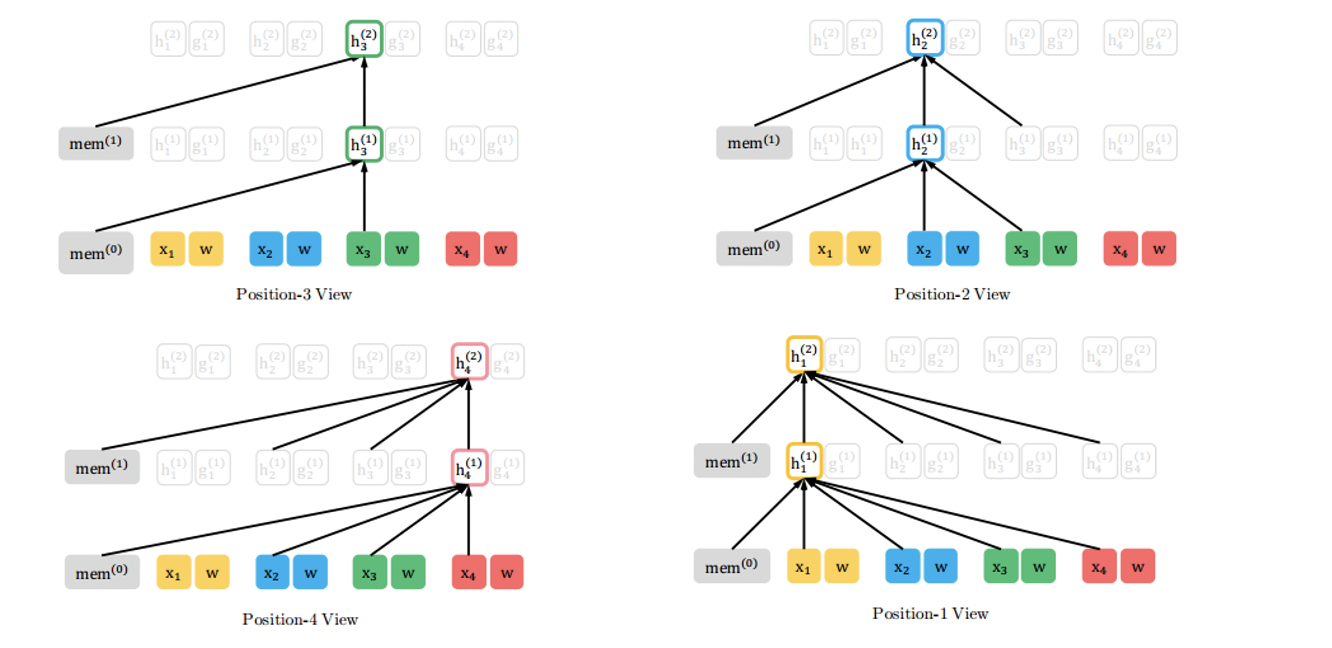
​   图示分析：暂时先不考虑图中的mem的含义。对于排列[3,2,4,1]，我们看左上图，第三个位置只看到了他自己（只和自己相连接）；右上图，第二个位置能看到位置2和位置3（和位置2位置3相连）；左下图，第四个位置能够看到位置2、3、4；右下图，位置1能够看到所有的节点。

​   看到右下图，你是不是想到了什么？是的，BERT。让我们回到图三（自注意力机制图示），我们看到，每一个节点都和上一层的所有节点连接，而右下图的节点一也做到了和上一层所有节点相连。在某种意义上，BERT和XLNet的结构在某种程度上是相同的！

​   鉴于上述结论，为了更加清楚的了解排列语言模型，我们换个角度出发。考虑一个具体的例子：
$$\begin{array}{rl}& 输入：Iamsohandsome\\ & BERT掩码输入：I[mask][mask]handsome\\ & XLNet随机选取的一个排列：[4,1,2,3]\end{array}$$
​   很显然，BERT的任务是预测出am和so；对于XLNet任务，我们同样的规定，只预测最后两个单词，也就是位置2和位置3，对应的单词也就是am和so。这样，BERT和XLNet的目标就相同了，有利于我们对比他们之间的相似和区别。

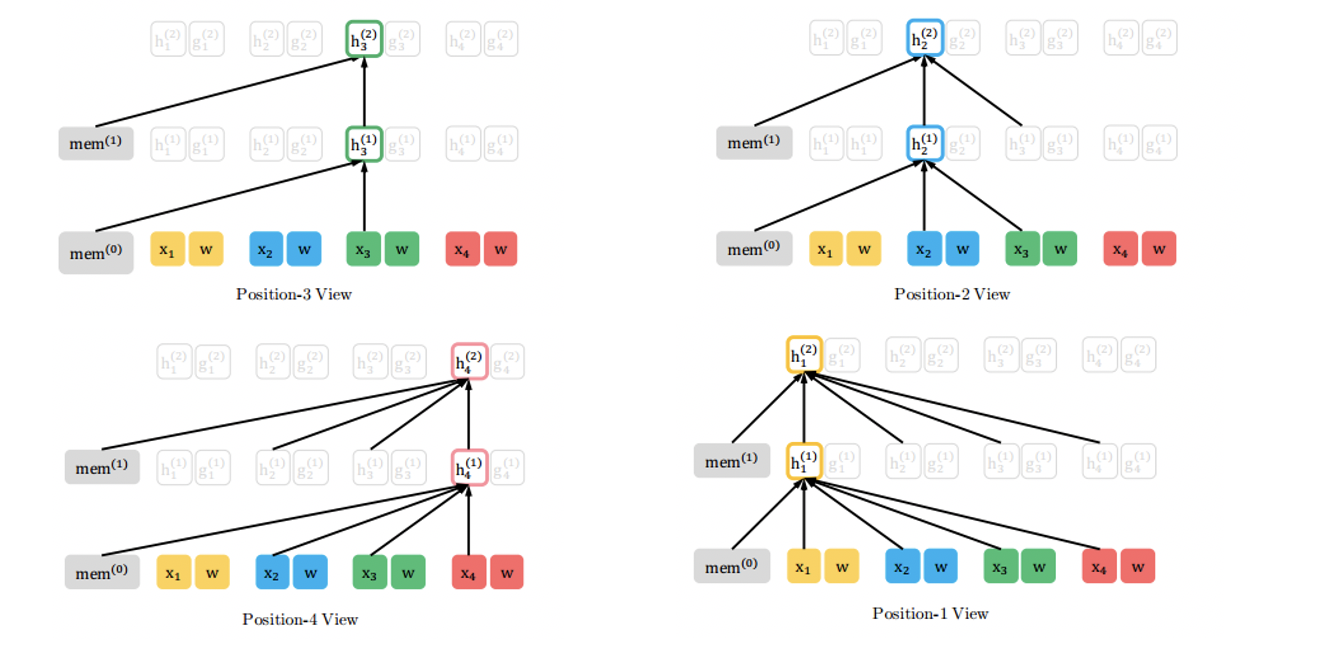
​   图示分析：怎么样，是不是很相似？我们逐个分析一下。首先是BERT，我们在预测第一个单词“am”时（红色圈），表面上看起来这个红色圈和上一层的每一个单词都相连，但实际上，上一层有两个单词是mask的，因此即使相连，你也看不到里面的信息（这就是上文中提到的词语独立性假设，也是BERT的缺点之一）。

​    然后是XLNet。根据[4,1,2,3]这个排列，我们在预测第一个单词am时，看不到so（注意图中红线并不是全联接的）。但是我们在预测"so"时，却可以看到"am"，因为和BERT不同，这里没有mask。所以XLNet的优点在这里就体现出来了：1、能看到上下文信息。2、没有词语独立性假设，预测的单词可以看到上一个预测的单词，BERT做不到这一点。

​    我在阅读文章的时候，出现了这样一个困惑，在这里解释一下。对于XLNet，第二层的红色圈并没有和上一层的“so”相连接，那么是不是意味着红色圈和“so”的参数没有得到训练呢？答案是肯定的。但是，也仅限在这个排列中，红色圈与与第三个位置的“so”没有训练到参数；这并不意味着二者之间没有参数，只是在这个排列中没有得到更新，在其它排列中有可能是得到更新的

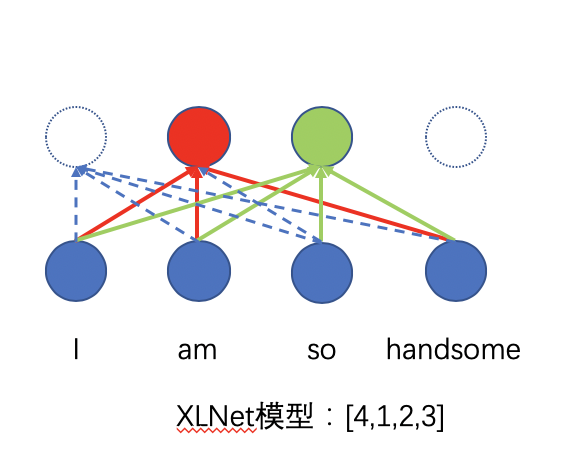
​    如图八所示，实线是这个排列中实际参与训练的参数，虚线的在这个排列中不参与训练，但是他们是存在的，可能会在其它排列中得到训练（图中虚线并没有画完，最右边的虚线圈和下面所有圈也是相互连接的，且是虚线连接）。因此可以得到一个结论，**每个位置都会和其他位置相连接，都会训练到相关的参数，只是在某个排列中，并不一定所有的参数参与训练而已。**例如对于[4,3,2,1]这个排列，位置2就会位置3相连接，参数就会得到训练。（注意这里的相连接，其实是计算注意力）。

​   再深入思考一下，其实BERT也具有这个问题。例如在上例中，由于“am”和"so"被mask，所以第二个位置和第三个位置在这里是训练不到的，但是在其它样例中，被mask的位置就有可能不是2和3了，这样此样例不会被训练到的参数在其它样例中就会参与训练。从这个角度来看，XLNet和BERT越来越像了。

3、排列语言模型的实现

​   上面我们已经讨论了排列语言模型的优点，就是能看到上下文信息，且没有词语独立性假设。下面就是如何实现的问题了。看起来排列语言模型挺简单的，只要随机选取一个排列，输入建模就完事了。但是，事实上并没有那么简单：简单的实现会导致很多问题，下面逐个分析产生的问题。

​   问题一：真实的输入是排列后的顺序吗？例如，对于[I am so handsome]，如果排列顺序是[2,3,4,1]，那么输入是[am, so, handsome, I]吗？

​   答案：显然不是。一是从我们上面的图可以看出，顺序并没有打乱。二是我们在预测的过程中，输入的是一个正常的句子，是不需要排列的。那么是怎么实现排序模型的呢？很简单，就是attention mask：随着正常输入进去的，还有attention mask，而根据attention mask可以知道排列顺序，如图所示：

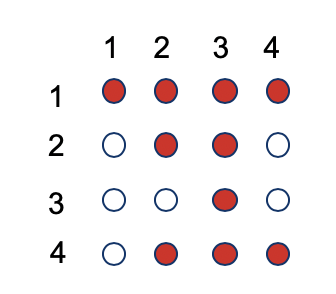
​   图示分析：红色代表可看见（相互连接，计算attention权重），1的四个圈都是红色的，说明和四个词语都是相连接的，因此1一定是排列中的最后一个元素。同样的，4能看见3个元素，因此4是倒数第二个元素。。。当然，具体的代码实现我还没有看，以后有时间回去研究一下。

​   问题二：考虑两个分解顺序[2,3,1,4]和[2,3,4,1]。假设我们都要预测第三个位置词语等于单词w的概率，可以计算如下
$$\begin{array}{r}顺序1=p(x_1=w|x_3{x}_2)=p(x_4=w|x_3{x}_2)=顺序2\end{array}$$
​   这显然不科学，**不同位置等于同一个词的概率怎么会相同呢？**那么造成这种问题的原因是什么呢？我们可以追溯到自回归模型的公式,如下所示。
$$\begin{gathered} log{P}_{\theta }(x)=log\prod _{t=1}^{T}p(x_t|x_{<t})=\sum _{t=1}^{T}log\frac{exp(h_{\theta }(x_{1:t-1}{)}^{T}e(x_t))}{{\sum }_{x^{,}}exp(H_{\theta }(x_{1:t-1}{)}^{T}e(x^{,}))} \\ 我们发现，预测x_t时，并没有用到位置信息。按照上例来说，我们在预测x_1时，并不知我们要预测第一个位置，预测 \\ {x}_4时，并不知我们要预测第4个位置，所以二者才会想等。因此解决办法就是加入预测的位置信息，区分不同位置。 \end{gathered}$$
​ 加入位置信息后，如下面的公式所示：
$$\begin{gathered} log{P}_{\theta }(x)=log\prod _{t=1}^{T}p(x_t|x_{<t})=\sum _{t=1}^{T}log\frac{exp(g_{\theta }(x_{1:t-1},z_t{)}^{T}e(x_t))}{{\sum }_{x^{,}}exp(g_{\theta }(x_{1:t-1},z_t{)}^{T}e(x^{,}))} \\ 看到没，原先的h变成了g，且参数包含了位置信息z_t，在分解顺序1中，z_3=1，在分解顺序2中，z_3=4 \end{gathered}$$
​    上述的两个问题都解决了，我们就得到最终的目标函数，就是上面的式子，下面的重点就是在于g怎么表达，g在神经网络中应该是怎样的一个形式？于是乎，我们就来到了XLNet最后一个知识点，也就是双流注意力机制。值得注意的是，双流注意力机制是为了解决上述设计的一个缺陷而提出的，要不然直接用正常的注意力就完事了。那么这个缺陷是什么呢，很简单：
$$\begin{gathered} 对于输入[I,am,so,handsome],假设分解顺序是[2,3,1,4],也就是[am,so,I,handsome] \\ 再次强调一下，真正的输入是正常的，并不是乱序的，乱序是通过attentionmask实现的，这里写成乱序只是为了方便 \\ 假设我们只预测后面两个词语，也就是I和handsome。 \\ 1、预测I时，我们不应该知道I，如果知道是I，也就是用到了I的信息，再去预测I，还有什么意义？ \\ 2、预测handsome时，我们应该知道I，因为根据自回归模型，预测一个词语啊，应该知道其上文 \end{gathered}$$
​   看明白了没有？1和2是矛盾的！（可能讲的有点乱，建议结合论文食用）。总结起来就一句话，预测某个词语A不能知道事先词语A，否则预测就没意义了；预测A后面的单词B，就需要知道A，因为预测B需要上文信息。双流自注意力机制就是为了解决上述的缺点。（双流自注意力机制实现了上述目标函数的同时，也解决了这个缺陷）。那么对于分解顺序[3,2,4,1],具体实现就是如下：

​    1、content representation：就是正常的注意力机制。图中的h

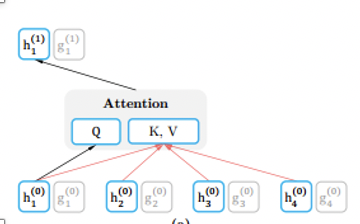
​   位置1由于在排列的最后，能看到所有的信息，包括等待预测的自己的所有信息

​   2、query representation：只能看到等待预测的位置信息，却看不到内容信息，图中的g

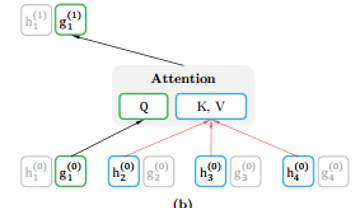
$$\begin{gathered} 比较一下两个图，并分析。h是正常的注意力机制，包含内容信息和位置信息 \\ g是queryrepresentation，包含上文的内容信息和位置信息，包含待预测词语的位置信息，但是不包含待预测词语的内容信息 \\ 上图很简单，不分析。看下图，Query是g_1^0(上标代表层数，下标代表位置) \\ Key和Value是h_2^0,h_3^0,h_4^0,就是没有h_1^0,因为h_1^0包含待预测词语的内容信息。 \end{gathered}$$
  用公式表达就是如下：

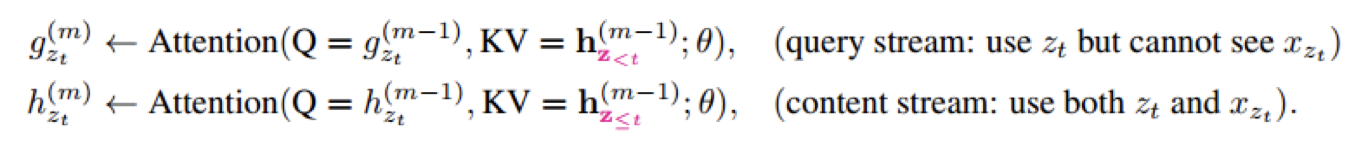
  这样，图中的g就是只包含待预测词语的位置信息，不包含待预测词语的内容信息，正符合我们的要求。这个g也就是我们最终目标函数中的g。

​   在这里放一张全图。

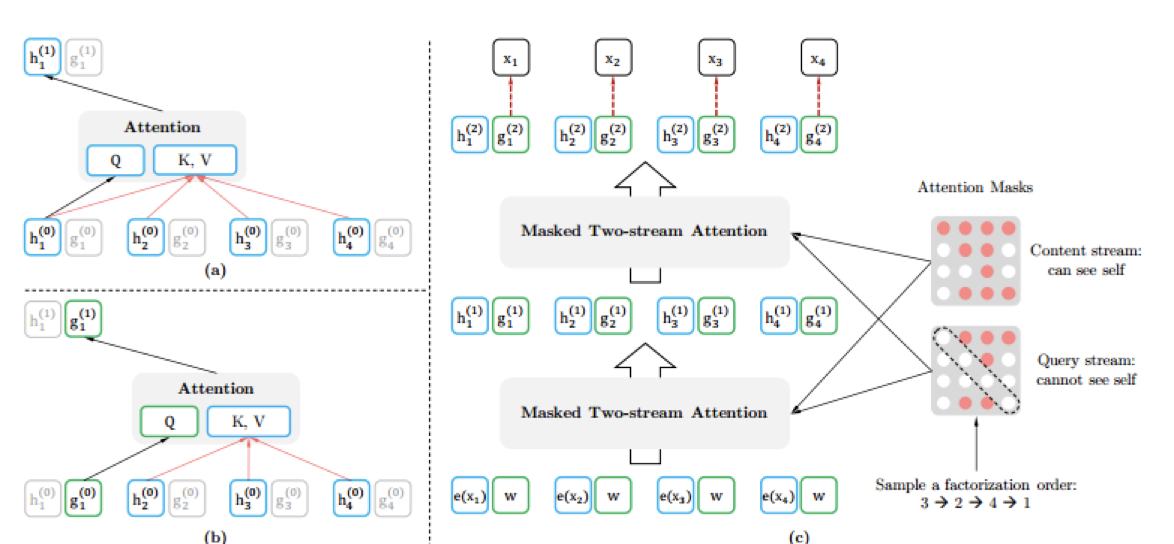
​   讲到这里，基本就结束了，但还有几个小点需要解释一下。

  1、训练的时候，用g预测某个位置的单词。但是训练结束，真正用到下游任务时，我们是不需要g的，只留下h即可。h就包含了丰富的上下文信息。也就是g只是为了训练用，只是为了训练h的参数，真正使用时，是要用h的。

  2、不知道有没有人有这么个疑问，为什么BERT使用正常的注意力不会出现最后那个问题呢？因为BERT的掩码，你都盖住了待预测词语，怎么会看到待预测预测的内容信息。而XLNet没有mask，如果不处理的话，会看到待预测词语的内容信息。

  3、XLNet在真正的训练中确实是只预测最后几个单词，是按照一个的方法来决定预测几个单词的。

四、总结

  ​ 你以为XLNet结束了，其实没有。你没有想过为什么叫XLNet吗？因为他接见了Transformer-xl的思想。所以想要全面了解XLNet，还需要去了解Transformer-xl的思想。但是对于本文来说，我们的重点应该在于XLNet的思想，对于Transformer-xl，那就看本文的反馈如何再决定是否更新了。

​   本文花了我一个周去写和调研资料，真的很辛苦。就这还是没看源码，看了源码之后才是真正的了解，对于源码的分析，都是后话吧。XLNet的网上资料很多，我都看了一下，发现天下文章一大抄，总共就两个流派，一个流派是CSDN上广为流传的那个，写的还不错，但不知到原作者是谁。另一个则是张成俊老师的文章，本文就是在他的影响下写的，与BERT的对比也是在他文章的启发下写出来的。

​

最后

以上就是专一山水为你收集整理的XLNet模型四、总结的全部内容，希望文章能够帮你解决XLNet模型四、总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。