1.1 统计学习
1、统计学习方法的三要素:模型、策略和算法
2、统计学习的方法是基于数据构建统计模型从而对数据进行预测与分析。
3、统计学习由监督学习、非监督学习、半监督学习和强化学习等组成。
1.2 监督学习
1、监督学习的任务是学习一个模型,使模型能够对任意给定的输入,对其相应的输出做出一个好的预测。
2、输入变量与输出变量均为连续变量的预测问题称为回归问题;输出变量为有限个离散变量的预测问题称为分类问题;输入变量与输出变量均为变量的序列的预测问题称为标注问题。
1.3 统计学习三要素
统计学习方法都是由模型、策略和算法构成的。
方法=模型+策略+算法
1.3.1 模型
1、在监督学习中,模型就是所要学习的条件概率分布或决策函数。模型的假设空间包含所有可能的条件概率分布或决策函数。
1.3.2 策略
有了模型的假设空,统计学习接着需要考虑的是按照什么样的准则学习或选择最优的模型。统计学习的目的在于从假设空间中选取最优模型。
损失函数度量模型一次预测的好坏,风险函数度量平均意义下模型预测的好坏。
1、损失函数和风险函数
预测值f(X)与真实值Y可能一致,也可能不一致,用一个损失函数或代价函数来度量预测错误的程度。损失韩式是f(X)和Y的非负实值函数,记作L(Y,f(X)).
常用的损失函数如下:
(1)0-1损失函数
(3)绝对损失函数
(4)对数损失函数或对数似然损失函数
2、损失函数值越小,模型就越好。由于模型的输入、输出(X,Y)是随机变量,遵循联合分布P(X,Y),所以损失函数的期望是
这称为风险函数或期望损失。
3、模型f(X)关于训练数据集的平均损失称为经验风险或经验损失,记作
4、经验风险最小化(ERM)的策略认为,经验风险最小化的模型是最优模型,根据这一策略,经验风险最小化求最优模型就是求解最优化问题:
5、极大似然估计就是经验风险最小化的一个例子。当模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化等价于似然估计。
6、当样本容量很小时,经验风险最小化学习的效果不好,会产生过拟合现象。为解决过拟合问题,提出了结构风险最小化的策略,结构风险最小化等价于正则化。结构风险最小化实在经验风险上加上表示模型复杂度的正则项或罚项。结构风险的定义是:
其中J(f)为模型的复杂度,模型f越复杂,复杂度J(f)就越大,反之,模型f越简单,复杂度J(f)就越小。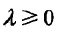
7、结构风险最小化的策略认为结构风险最小的模型是最优的模型。所以求最优模型,就是求解最优化的问题:
1.4 模型评估与模型选择
1、通常将学习方法对未知数据的预测能力称为泛化能力。
2、模型选择时,不仅要考虑对已知数据的预测能力,而且还要考虑对未知数据的预测能力。
1.5 正则化与交叉验证
1.5.1 正则化
模型选择的典型方法是正则化。正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项或者罚项。正则化一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大。比如,正则化项可以是模型参数向量的范数。
正则化一般具有如下形式:
其中,第一项是经验风险,第二项是正则化项,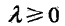
正则化项可以取不同的形式。例如,回归问题中,损失函数时平方损失,正则化项可以是参数向量的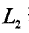
注:简单说,0范数表示向量中非零元素的个数;1范数表示为向量元素绝对值之和;2范数表示向量元素的平方和再开方。
正则化的作用是选择经验风险与模型复杂度同时较小的模型。
1.5.2 交叉验证
另一种常用的模型选择方法是交叉验证。
如果样本充足,进行模型选择的另一种方法是随机地将数据集切分成训练集、验证集和测试集。训练集用来训练模型,验证集用于模型的选择,而测试集用于最终对学习方法的评估。
但是,大部分应用中数据集是不充足的。为了选择好的模型,可以采用交叉验证方法。交叉验证的基本思想是重复地使用数据;把给定的数据进行切分,将切分的数据集组合为训练集和测试集,在此基础上反复的进行训练、测试以及模型的选择。
1、简单交叉验证
简单交叉验证方法是:随机的将数据集分为两部分,一部分作为训练集,另一部分作为测试集。
2、S折交叉验证(应用最多)
方法是:首先随机地将已给的数据切分为S个互不相交的大小相同的子集;然后利用S-1个子集的数据训练模型,利用余下的子集测试模型;将这一过程对可能的S种选择重复进行;最后选出S次评测中平均测试误差最小的模型。
3、留一交叉验证
S折交叉验证的特殊情况是S=N,称为留一交叉验证,往往在数据缺乏的情况下使用,N是给定数据集的容量。
1.6 泛化能力
学习方法的泛化能力是指由该方法学习到的模型对未知数据的预测能力。
1.6.1 泛化误差
模型对未知数据预测的误差就是泛化误差。事实上,泛化误差就是模型的期望风险。
1.7 生成模型与判别模型
监督学习方法可以分为生成方法和判别方法,所学到的模型分别称为生成模型和判别模型。
生成方法由数据学习联合概率分布P(X,Y),然后求出条件概率分布P(Y|X)作为预测的模型,即生成模型:
这样的方法之所以称为生成方法,是因为模型表示了给定输入X产生输出Y的生成关系。典型的生成模型有:朴素贝叶斯法和隐马尔可夫模型。
判别方法由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测的模型,即判别模型。判别方法关心的是对给定的输入X,应该预测什么样的输出Y。典型的判别模型包括:k近邻法、感知机、决策树、逻辑斯蒂回归、最大熵模型、支持向量机、提升方法和条件随机场等。
1.8 回归问题
1、回归用于预测输入变量和输出变量之间的关系。回归模型表示从输入变量到输出变量之间的映射的函数。
2、回归问题按照输入变量和输出变量之间关系的类型即模型的类型,分为线性回归和非线性回归。
线性回归和非线性回归的区别:通过指数来进行判断即可,线性回归就是每个变量的指数都是1(一次方),为直线形态,而非线性回归就是至少有一个变量的指数不是1(二次方或多次方),为曲线形态。
最后
以上就是俭朴金针菇最近收集整理的关于《统计学习方法》总结 第1章-统计学习方法概论1.1 统计学习1.2 监督学习的全部内容,更多相关《统计学习方法》总结内容请搜索靠谱客的其他文章。
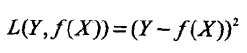
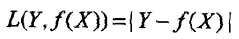


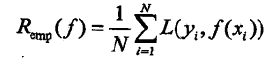


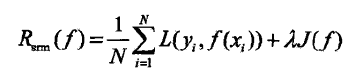

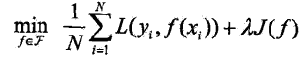

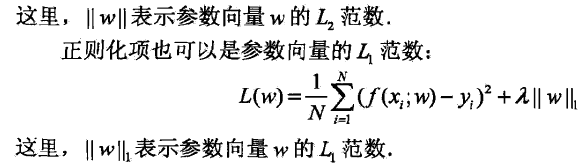

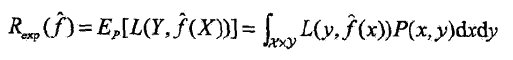
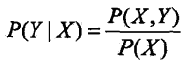








发表评论 取消回复