使用simhash算法对网页去重

如果搜索文档有很多重复的文本，比如一些文档是转载的其他的文档，只是布局不同，那么就需要把重复的文档去掉，一方面节省存储空间，一方面节省搜索时间，当然搜索质量也会提高。
simhash是google用来处理海量文本去重的算法。

1. 原理：

simhash将一个文档转换成一个64位的字节，暂且称之为签名值，然后判断两篇文档的签名值的距离是不是小于等于n（根据经验这个n一般取值为3），就可以判断两个文档是否相似。

2. simhash和传统的hash算法有什么不同？

simhash和传统的hash都可以将文档转换为一个签名值，它们有什么不同呢？
simhash基于局部敏感哈希框架，即如果两个文档内容越相似，则其对应的两个哈希值也越接近，所以就可以将文本内容相似性问题转换为哈希值的相近性问题。
而传统的hash算法只负责将原始内容尽量均匀随机地映射为一个签名值，原理上相当于伪随机数产生算法。产生的两个签名，如果相等，说明原始内容在一定概率下是相等的；如果不相等，除了说明原始内容不相等外，不再提供任何信息，因为即使原始内容只相差一个字节，所产生的签名也很可能差别极大。而simhash的签名值除了提供原始内容是否相等的信息外，还能额外提供不相等的原始内容的差异程度的信息。

3. simhash算法步骤描述：

simhash算法步骤见下图：

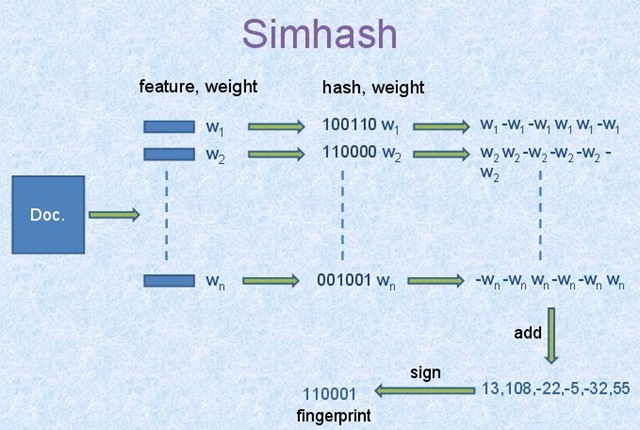
1）首先从文档内容中抽取n个能表征文档的特征，至于具体实现，则可以采用不同的抽取方法，经过此步骤，获得文档的特征词及其权值对，即图中的n个(feature,weight)。方法之一可以参考 使用向量空间模型（df-idf）计算搜索文档与查询词的相关性中的（6）使用TF*IDF框架提取文档和用户查询的特征词及其权重。
2）利用一个哈希函数将每个特征词映射成bit_count位的二进制数值。图中所示算法将每个特征词转换为了bit_count=6的二进制数值，这样每个（feature，weight）就转换为图中的（hash，weight）了。
3）利用权重改写特征的二进制hash值，将权重融入其中，将bit_count位的二进制数值改写为bit_count个实数，形成一个实数向量。假设某个特征的权值是w，则对二进制向量做如下改写：如果二进制的某个比特位是数值1，则实数向量中对应位置改写为数值w；如果比特位数值为0，则实数向量中对应位置改写为数值-w，即权值的负数。通过以上规则，就将bit_count的二进制数改为了特征权重的实数向量。
4）当n个特征都进行了上述改写后，对所有特征的实数向量累加获得一个代表文档整体的实数向量。累加规则也很简单，就是将对应位置的数值累加即可。
5）再次将实数向量转换为bit_count位的二进制数值。转换规则如下：如果对应位置的数值大于0，则设置为二进制数字1；如果小于等于0，则设置为二进制数字0。如此就得到了文档的信息指纹，即最终的simhash值。
上图将文档特征词hash为6位的二进制数值，在实际计算中，往往会将长度设定为64，即每个文档转换为64比特的simhash值。

4. 利用simhash对文档去重

将文档转换为simhash值后，如何利用simhash值比较两个文档的相似性呢？对于两个文档A和B，其内容相似性可以通过比较simhash值的差异来体现，内容越相似，则二进制数值对应位置的相同的0或者1越多，两个二进制数值不同的二进制位数称为“海明距离”（也就是两个二进制数值xor 后二进制中1的个数）。
举例如下：

A = 100111;
B = 101010;
hamming_distance(A, B) = count_1(A xor B) = count_1(001101) = 3;

当我们算出所有文档的simhash值之后，需要计算文档 A和文档 B之间是否相似的条件是：A和B的海明距离是否小于等于n。
一般对于64位二进制数来说，判断两个文档是否近似重复的标准是：海明距离是否小于等于3，如果两个文档的二进制数值小于等于3位不同，则判定为近似重复文档。

5. simhash的c++实现：

1）https://github.com/yanyiwu/simhash （读过）
2）https://github.com/seomoz/simhash-cpp （未读）
两者将字符串hash为64位数都是使用jenkins hash

6. 处理海量文档

1）利用hash查找海量simhash（一）
海量的网页经过上述步骤，转换为海量的二进制数值，此时如果新抓取到一个网页，如何找出近似重复的内容呢？
一个很容易想到的方式是一一匹配，将新网页转换为64比特的二进制数值，之后和所有网页的simhash一一比较，如果两者的海明距离小于等于3，则可以认为是近似重复网页。这种方法虽然直观，但是计算量过大，所以在以亿计的网页中，实际是不太可行的。
假设我们要寻找海明距离3以内的数值，根据抽屉原理，只要我们将整个64位的二进制串划分为4块，无论如何，匹配的两个simhash之间至少有一块区域是完全相同的，所以我们可以借鉴hash查找的方法，把这一区域的数值作为key，先找到哪些simhash的key等于目标simhash的key，然后在这些simhash集合中查找那些海明距离在3以内的数值。
这就要求我们在存储simhash时，需要把key相同的simhash存储在一起。
但又因为我们无法事先得知完全相同的是哪一块区域，所以四个区域的每个区域都应该作为我们查找value的key值。
具体做法如下：

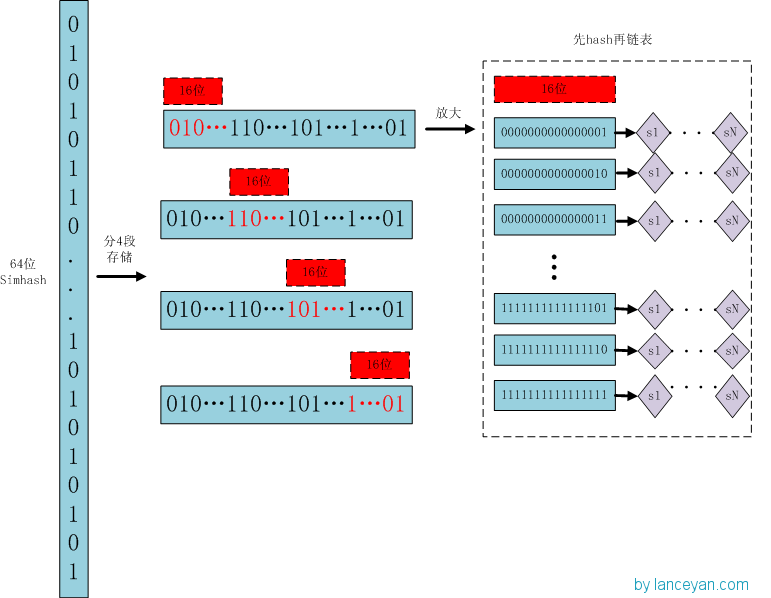
存储：
1）将64位的simhash code平均分成4个区域，每个区域都有16bit。（图上红色的16位）
2）分别以4个16位二进制码作为key，查找该key对应位置上是否有元素。（放大后的16位）
3）对应位置没有元素，直接追加到链表上；对应位置有则直接追加到链表尾端。（图上的 S1 — SN）
查找：
1）将需要比较的simhash code拆分成4个16位的二进制码。
2）分别以4个16位二进制码作为key，查找simhash集合每个key对应位置上是否有元素。
3）如果有元素，则把链表拿出来顺序查找比较，查找那些海明距离小于3的数值，整个过程完成。
2）空间和时间开销（一）
这种方法，由于每个hashcode最多有4个key（显然如果有两个区域的code值相同，则key小于4个），每个key都要存储一遍，所以需要的空间是原来的4倍。但每个key对应的simhash平均数量变为simhash数量总和的 1/216 ，所以搜索时间是一一搜索的 4216 。
3）利用hash查找海量simhash（二）
假设我们还是要寻找海明距离3以内的数值，如果我们要把4个区域变成5个区域，所花的空间和时间又变成多少呢？
因为根据抽屉原理，如果分成5个区域，则至少有两个区域是完全相同的，所以需要将这两块区域的值作为key，查找时先找到哪些simhash的key等于目标simhash的key，然后在这些simhash集合中查找那些海明距离在3以内的数值。
究竟是哪两块区域相同共有 C25 =10种情况，所以两个区域组成的这10个key都应该作为我们查找value的key值。
具体做法如下：
存储：
1）将64位的simhash code分成5个区域，每个区域分别有13 13 13 13 12位。
2）分别以10种26位（13+13）或25位（13+12）二进制码作为key，查找该key对应位置上是否有元素
3）对应位置没有元素，直接追加到链表上；对应位置有则直接追加到链表尾端
查找：
1）将需要比较的simhash code分成5个区域，每个区域分别有13 13 13 13 12位。
2）分别以10种26位（13+13）或25位（13+12）二进制码作为key，查找simhash集合对应key位置上是否有元素。
3）如果有元素，则把链表拿出来顺序查找比较，查找那些海明距离小于3的数值，整个过程完成。
4）空间和时间开销（二）
这种方法，由于每个hashcode最多有10个key，每个key都要存储一遍，所以需要的空间是原来的10倍。但每个key对应的simhash平均数量为simhash数量总和的 1226 或 1225 ，所以搜索时间是一一搜索的 10226 或 10225 。

7. 存储simhash的数据结构：

根据6，存储simhash需要用的数据结构应该为：hash < int,vector < uint_64>>吧。

8. 参考：

1）《这就是搜索引擎–核心技术详解10.4》
2）《simhash算法原理及实现》
3）《海量数据相似度计算之simhash短文本查找》
4）《我的数学之美系列二 —— simhash与重复信息识别》
5）google发布的simhash论文：《Detecting near-duplicates for web crawling》
6）google讲解simhash的ppt《Detecting Near-Duplicates for Web Crawling》
7）《Simhash算法原理和网页查重应用》

最后

以上就是昏睡航空为你收集整理的使用simhash算法对网页去重的全部内容，希望文章能够帮你解决使用simhash算法对网页去重所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。