https://www.cnblogs.com/gaoxiang12/p/5113334.html
前言
转眼间一个学期又将过去,距离我上次写《一起做RGBD SLAM》已经半年之久。《一起做》系列反响很不错,主要由于它为读者提供了一个可以一步步编码、运行的SLAM程序,为读者理解SLAM实现的细节作了详细的介绍。但是我也有很多对它不满意的地方。作为面向实现的介绍,它的代码不够稳定可靠,例如,甚至没有对匹配丢失的情况进行处理,因而只能用于教学。另一方面,对SLAM研究者来说,我只是介绍了编码方面如何调用一些常见的库函数,而没有对这些函数进行深入的,原理上的讲解。这就导致了读者只了解了函数的接口,而没法根据数学原理进行创新。归根到底,研究机器人相关问题,一是要有扎实的数学基础,二是要有强大的动手编程能力,这对大多数刚入门的研究者来说,极具挑战性。我也希望,通过阅读我的博客,你能走进SLAM研究的门槛,有朝一日自己也写出优秀的程序和论文。
有鉴于此,我准备写一写SLAM相关的数学知识,包括代数、几何、概率、运筹等等。对于重要的算法例如ICP,EKF,细致讨论它的原理,并给出它的实现(原生的代码或在某个库的实现)。由于它们的原理较复杂,我会从最基本的东西开始讲起。但是我毕竟不是在写数学书,我不会像数学书那样写成``定义——定理——推论”的结构。我们不会纠缠于一些定理的严格证明,相反的,我们只在必要的情况下加以说明,告诉读者这些数学公式在SLAM中有何应用,如何应用。
由于博客编辑器的限制,我们以斜体字xx表示变量,以粗正体AA表示矢量和字母,以黑板粗体ℝR表示空间。希腊字母没有粗体所以保持原样。向量默认为列向量。其余和普通的数学书一致。
小萝卜:师兄,这么严肃不是你的风格啊!
师兄:啊,数学嘛……
刚体运动
本篇我们讨论一个很基础的问题:如何描述机器人的位姿。这也是研究SLAM的第一个问题。注意这里“位姿”的用语包含了位置和姿态。描述位置是很简单的。如果机器人在平面内运动,那么用两个坐标来描述它的位置:
x=[x,y]T.x=[x,y]T.
相应的,如果它在三维空间中,我们就用三个空间坐标来表示:
x=[x,y,z].x=[x,y,z].
姿态的表达比点稍为复杂。2D的姿态可以只用一个旋转角θθ表达。3D姿态的表达方式则有多种。常见的如欧拉角、四元数、旋转矩阵等。我们将在后文详细介绍。有了位置和姿态,我们就可以描述一个坐标系。进一步,还能描述坐标系间的变换关系。常见的问题如:机器人视野中某个点,对世界坐标系的(或地图的)哪个点?这时,就需要先得到该点针对机器人坐标系坐标值,再根据机器人位姿转换到世界坐标系中。
齐次坐标系
在位姿转换中,通常采用射影空间的齐次坐标表示。齐次坐标是什么呢?记nn维射影空间为ℙnPn,其中一个空间点的坐标为普通的3D坐标加一个齐次分量:
x=[x1,…,xn,w]T.x=[x1,…,xn,w]T.
例如,在2维和3维射影空间中的点,分别表示为:
x2D=[x,y,w]Tx3D=[x,y,z,w]T(1)(1)x2D=[x,y,w]Tx3D=[x,y,z,w]T
小萝卜:既然一个空间点只有3个坐标,为啥非要用四个数表示呢?
师兄:嗯,四个数表示点,说明点和坐标肯定不是一一对应的。没错,在齐次坐标中,某个点xx的每个分量同乘一个非零常数kk后,仍然表示的是同一个点。因此,一个点的具体坐标值不是唯一的。如[1,1,1,1]T[1,1,1,1]T和[2,2,2,2]T[2,2,2,2]T是同一个点。但在w≠0w≠0时,我们可以对每个坐标除以最后一项ww,强制最后一项为1,从而得到一个点唯一的坐标表示:
x3D=[x/w,y/,z/w,1]T(2)(2)x3D=[x/w,y/,z/w,1]T
这时,忽略掉最后一项,这个点的坐标和欧氏空间就是一样的。那么,为要用齐次坐标呢?原因有以下几条。
- 齐次坐标下点和直线(高维空间里为超平面)能够使用同样的表达。
例如,3D空间ℝ3R3中,一个平面ππ可由一个方程定义:
π:ax+by+cz+d=0(3)(3)π:ax+by+cz+d=0
则该平面ππ可以用ℙ3P3中的坐标π=[a,b,c,d]Tπ=[a,b,c,d]T来描述。这样,点位于平面上(2D对应点位于直线上)的事情可以简洁地表示为:
πTx=0.(4)(4)πTx=0.
把点和超平面采用同样的表示,这种做法一个非常直接的好处,是射影几何里的“对偶原理”。该原理是说,任何有关“点”与“平面”的命题,都可以交换“点”与“平面”的概念,得到一个对偶的命题。对偶命题和原命题是一样的。通过“对偶原理”,射影几何的数学家就可以偷懒,只需要证一半定理,因为对偶命题和原命题有同样的涵义。例如,我们证明了ℙ2P2中某条件下三点共线,那么替换概念后的三线共点则自然成立。
小萝卜:数学家真是好懒啊!
- 齐次坐标能囊括无穷远点与无穷远超平面。
最后一项坐标为零的点称为无穷远点,它们在ℙnPn中真实存在,且能够很方便地参与正常的代数运算。根据式44,易见所有无穷远点都在一个平面π∞=[0,0,0,1]Tπ∞=[0,0,0,1]T上,该平面记作无穷远平面(2D对应无穷远直线)。
ℙ2P2中的无穷远直线较容易理解。它就像是地平线,与所有直线相交于位于它之上的无穷远点。而且,在射影变换中(例如照相),很容易在照片中看到地平线并算出它的方程。这说明2D射影变换会把无穷远线变成通常的直线。
- 齐次坐标可以方便地将平移与旋转放在一个矩阵中。
师兄:这应该是最明显的好处啦!大家都爱用齐次坐标,包括我。有关坐标系怎么用齐次坐标进行变换,后文会详细解释。现在我们能表达点了,还剩下一个姿态。由于2D与3D差别较大,我们分而述之。
2D姿态的描述
2D空间中,物体的位姿可用两个平移量tx,tytx,ty加一个旋转角θθ表示,如下图所示。此时,设机器人坐标系O′−X′−Y′O′−X′−Y′下某点的坐标为[xr,yr]T[xr,yr]T,对应在世界坐标系O−X−YO−X−Y下为[xw,yw]T[xw,yw]T,那么由直观推得:
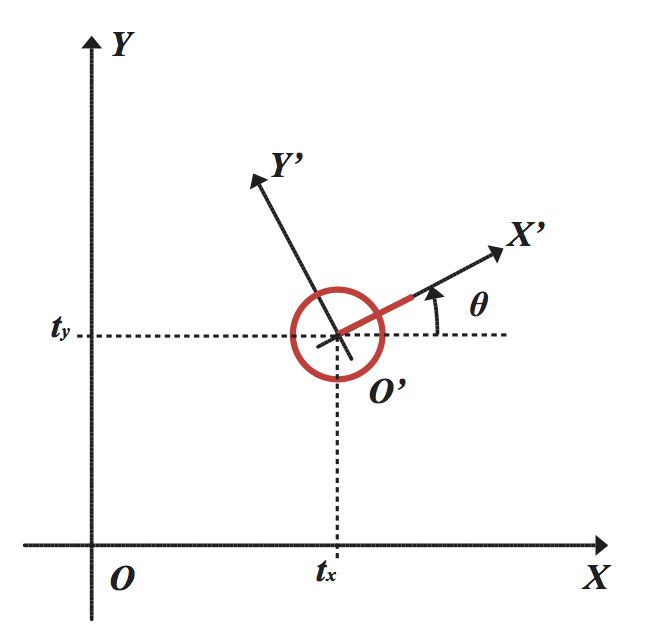
{xw=xrcosθ−yrsinθ+txyw=xrsinθ+yrcosθ+ty(5)(5){xw=xrcosθ−yrsinθ+txyw=xrsinθ+yrcosθ+ty
读者可以自行尝试推导一下,在虚线处建立一个中间坐标系即可。若将该式写成矩阵形式,则有:
xw=Rxr+t(6)(6)xw=Rxr+t
其中
R=[cosθsinθ−sinθcosθ],t=[tx,ty]TR=[cosθ−sinθsinθcosθ],t=[tx,ty]T
RR称为旋转矩阵,tt为平移矢量。注意到RR是一个正交矩阵,且只有一个自由度。加上平移矢量后,一共有三个自由度。
此定义下的旋转阵必是正交阵。而正交阵并非全是旋转矩阵。事实上,行列式为+1+1的正交阵才是旋转矩阵,行列式为−1−1的正交阵是镜像后的旋转矩阵。
式66中,xwxw和xrxr还不是线性关系。下面我们用齐次坐标表示它们,即:
xw=[xw,yw,1]T,xr=[xr,yr,1]Txw=[xw,yw,1]T,xr=[xr,yr,1]T
则有:
xw=[R2×20T1×2t2×1I1×1]xr(7)(7)xw=[R2×2t2×101×2TI1×1]xr
为便于理解,我们在矩阵下方标出了它的维数。可以看使用齐次坐标标满足了线性关系,记作:
xw=Tw,rxr(8)(8)xw=Tw,rxr
其中Tw,rTw,r表示从世界坐标系到机器人坐标系的变换矩阵。我们也可以轻松地写出反向的变换矩阵:
xr=Tr,wxw=T−1w,rxw=[R−10T−R−1t1]xw(9)(9)xr=Tr,wxw=Tw,r−1xw=[R−1−R−1t0T1]xw
既然如此,我们就可用TT表示机器人的位姿,那么机器人在时刻tt的位姿就可以记作TtTt。当然,从存储上来讲,存储TT是不经济的。在2D运动中,它有九个变量,但实际自由度只有三个。所以我们可以只存储位移矢量tt与旋转角θθ,而在需要计算的时候再构建出TT。称2D欧几里得变换,它对矩阵乘法构成群(群是一个集合加一种运算,且运算在该集合上满足封闭性、结合律、有单位元和逆元。),该群记作SE(2)SE(2)。相应的,二维旋转构成二维旋转群(或称特殊正交群)SO(2)SO(2)。有关它们进一步的性质,我们会在以后的李群、李代数中提到。
3D变换
3D的旋转可以由旋转矩阵、欧拉角、四元数等若干种方式描述,它们也统称为三维旋转群SO(3)SO(3)。而3D的变换即旋转加上位移,是为SE(3)SE(3)。为了和2D变换统一起见,我们首先介绍旋转矩阵表示法。
旋转矩阵描述
旋转矩阵是一种3×33×3的正交矩阵,它对变换的描述十分类似于2D情形。参照上一节的数学符号,我们有:
xw=[R3×30T1×3t3×111×1]xr(10)(10)xw=[R3×3t3×101×3T11×1]xr
这里RR为3D的旋转矩阵,同样的,tt为3D的平移矢量。
由于3D旋转都可以归结成按照某个单位向量nn进行大小为θθ的旋转。所以,已知某个旋转时,可以推导出对应的旋转矩阵。该过程由罗德里格斯公式表明,由于过程比较复杂,我们在此不作赘述,只给出转换的结果:
R(n,θ)=⎡⎣⎢⎢⎢n2x(1−cθ)+cθnxny(1−cθ)−nzsθnxnz(1−cθ)+nysθnxny(1−cθ)+nzsθn2y(1−cθ)+cθnynz(1−cθ)−nxsθnxnz(1−cθ)−nysθnynz(1−cθ)+nxsθn2z(1−cθ)+cθ⎤⎦⎥⎥⎥(11)(11)R(n,θ)=[nx2(1−cθ)+cθnxny(1−cθ)+nzsθnxnz(1−cθ)−nysθnxny(1−cθ)−nzsθny2(1−cθ)+cθnynz(1−cθ)+nxsθnxnz(1−cθ)+nysθnynz(1−cθ)−nxsθnz2(1−cθ)+cθ]
这里n=[nx,ny,nz]T,cθ=cosθ,sθ=sinθn=[nx,ny,nz]T,cθ=cosθ,sθ=sinθ。公式虽然较为复杂,但实际写成程序后,只需知道旋转方向和角度后即可完成计算。另一件有趣的事是,如果用
n∧=⎡⎣⎢⎢⎢0nz−ny−nz0nxny−nx0⎤⎦⎥⎥⎥n∧=[0−nznynz0−nx−nynx0]
表示与nn对应的一个反对称矩阵,那么有:
R(n,θ)=cosθI+(1−cosθ)nnT+sinθn∧=exp(θn∧)(12)(12)R(n,θ)=cosθI+(1−cosθ)nnT+sinθn∧=exp(θn∧)
最后那个指数,读者若不理解,可以暂时不管它,这将在之后的李代数中会讲到。根据此式,我们也可以从任意给定的旋转矩阵,求出对应的转轴与转角。关于转角θθ,我们对上式两边求矩阵的迹,可得:
tr(R)===cosθtr(I)+(1−cosθ)tr(nnT)+sinθtr(n∧)3cosθ+(1−cosθ)1+2cosθ(13)(13)tr(R)=cosθtr(I)+(1−cosθ)tr(nnT)+sinθtr(n∧)=3cosθ+(1−cosθ)=1+2cosθ
因此:
θ=arccos(12[tr(R)−1])(14)(14)θ=arccos(12[tr(R)−1])
关于转轴nn,由于旋转轴上的向量在旋转后不发生改变,说明
Rn=n.Rn=n.
因此,只要求此方程的解向量即可。这也说明nn是RR特征值为11的一个特征向量。
总之,读者应当明白在3D时,旋转和平移仍可用转移矩阵TT来描述,其结构也与2D类似。而T4×4T4×4构成了三维欧氏变换群SE(3)SE(3)。注意到TT虽然有16个变量,但真正的自由度只有6个,其中3个旋转,3个位移。
旋转矩阵描述是一种比较适合数学推导及计算机实现的方式,但它不符合人类的思维方式。当你看到一个3×33×3的矩阵时,很难想象物体实际上发生了怎样的旋转。反之,给定一个旋转方式,人也很难直接写出矩阵的数值。所以,为了便于人类理解,人们还使用了其他方法来表示三维旋转。
欧拉角
欧拉角是一种广为使用的姿态描述方式,以直观见长。在最常用的欧拉角表达方式中,我们把旋转分解成沿三个轴转动的量:滚转角-俯仰角-偏航角(roll-pitch-yaw)。它的好处是十分的直观,且只有三个参数描述。缺点是会碰到著名的万向锁问题:在俯仰为±90∘±90∘时,表达某个姿态的形式不唯一。此外,它也不易于插值和迭代。
我们并不会详细介绍欧拉角,因为它在SLAM中用处也很有限。我们既不会在数学推导中使用它,也不会在程序中用欧拉角表示机器人的姿态。不过,在您想验证自己算法输出的姿态是否有错时,转换成欧拉角能让你快速辨认结果是否有错。
四元数
四元数原理和各种运算将在下一篇博客中提到。
本篇小结
本篇博客介绍了2D和3D空间中刚体运动的表示方法,以旋转矩阵为主。下一篇我们将介绍四元数表示法,然后演示如何用Eigen3对这些矩阵进行操作。敬请期待。
最后
以上就是魔幻哑铃最近收集整理的关于视觉SLAM中的数学基础 第一篇 3D空间的位置表示的全部内容,更多相关视觉SLAM中的数学基础内容请搜索靠谱客的其他文章。








发表评论 取消回复