kd-tree详解

kd-tree适用的范围：

        二维平面最近点对之间的操作，动态维护、询问、查询等。包括曼哈顿距离和欧几里德距离。

曼哈顿距离和欧几里德距离：

1.曼哈顿距离

曼哈顿距离又称Manhattan distance，还见到过更加形象的，叫出租车距离的。具体贴一张图，应该就能明白。

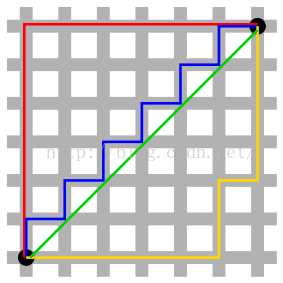
上图摘自维基百科，红蓝黄皆为曼哈顿距离，绿色为欧式距离。

2.欧式距离

欧式距离又称欧几里得距离或欧几里得度量（Euclidean Metric），以空间为基准的两点之间最短距离，只算在空间下。

说的通俗点，就是初中知识，两点之间直线最短的概念。

kd-tree讲解：

我们可以想象在平面上有N个点。首先，按横坐标排序找到最中间的那个点。然后水平划一条线，把平面分成左右两个部分。再递归调用左右两块。注意，在第二次（偶数次）调用的时候，是找到纵坐标中最中间的点，并垂直画一条线。

这样效率看上去很好。维护的时候有点像线段树。每个点记录它的坐标、它辖管的区间4个方向的极值、它的左右（或上下）的两个点的标号。递归两个子树时，注意要up更新这个点辖管的范围。

inline int cmp(arr a,arr b){return a.d[D]<b.d[D]||a.d[D]==b.d[D]&&a.d[D^1]<b.d[D^1];}//D代表竖着排还是横着排
inline void up(int k,int s)
{
  a[k].min[0]=min(a[k].min[0],a[s].min[0]);
  a[k].max[0]=max(a[k].max[0],a[s].max[0]);
  a[k].min[1]=min(a[k].min[1],a[s].min[1]);
  a[k].max[1]=max(a[k].max[1],a[s].max[1]);
}
int build(int l,int r,int dd)
{
  D=dd;int mid=(l+r)>>1;
  nth_element(a+l+1,a+mid+1,a+r+1,cmp);
  a[mid].min[0]=a[mid].max[0]=a[mid].d[0];
  a[mid].min[1]=a[mid].max[1]=a[mid].d[1];
  if (l!=mid) a[mid].l=build(l,mid-1,dd^1);
  if (mid!=r) a[mid].r=build(mid+1,r,dd^1);
  if (a[mid].l) up(mid,a[mid].l);
  if (a[mid].r) up(mid,a[mid].r);
  return mid;
}

插入点，也是类似于线段树的思想：

void insert(int k)
{
  int p=root;D=0;
  while (orzSYC)
  {
    up(p,k);
    if (a[k].d[D]<=a[p].d[D]){if (!a[p].l) {a[p].l=k;return;} p=a[p].l;}
    else {if (!a[p].r) {a[p].r=k;return;} p=a[p].r;}
    D^=1;
  }
}

int getdis(int k)
{
  int res=0;
  if (x<a[k].min[0]) res+=a[k].min[0]-x;
  if (x>a[k].max[0]) res+=x-a[k].max[0];
  if (y<a[k].min[1]) res+=a[k].min[1]-y;
  if (y>a[k].max[1]) res+=y-a[k].max[1];
  return res;
}
void ask(int k)
{
  int d0=abs(a[k].d[0]-x)+abs(a[k].d[1]-y);
  if (d0<ans) ans=d0;
  int dl=(a[k].l)?getdis(a[k].l):INF;
  int dr=(a[k].r)?getdis(a[k].r):INF;
  if (dl<dr){if (dl<ans) ask(a[k].l);if (dr<ans) ask(a[k].r);}
  else {if (dr<ans) ask(a[k].r);if (dl<ans) ask(a[k].l);}
}

getdis有点像Astar中的“估价函数”。计算（x，y）与当前点范围的差距有多少，然后按顺序遍历左二子和右儿子。这样，如果更新到最优值，就能及时退出。这种算法在随机数据上是lg的，但是在构造数据上约是sqrt的。

练习推荐：bzoj2648&& bzoj2716&&bzoj3053

最后

以上就是爱笑小天鹅为你收集整理的kd-tree详解的全部内容，希望文章能够帮你解决kd-tree详解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。