第一章 绪论
1.1 引言
人类可以对很多未知的事物作出有效的预判,是因为我们已经积累了许多经验,而通过对经验的利用,就能对心的情况作出有效的决策。
同样的预判能力,计算机能够完成吗?
机器学习正是这样一门学科,它致力于研究如何通过计算的手段,利用经验来改善系统自身的性能。机器学习所研究的主要内容就是“学习算法”,“学习算法”就是指计算机通过从数据中产生“模型”的过程。有了学习算法,我们为它提供数据,算法基于数据产生模型。产生的模型就可以完成类似于人类的预判能力。
(本书中的“模型”是指从数据中学习得到的结果)
1.2 基本术语
要进行机器学习,数据是必不可少的。
西瓜数据集:
(色泽=青绿;根蒂=蜷缩;敲声=清脆)、
(色泽=乌黑;根蒂=硬挺;敲声=清脆)、
。。。。。。。
样本(sample)/示例(instance):每一条记录了一个事件或者对象的数据记录称为一个样本。
数据集(data set):记录数据的集合。此例中,是指包含了所有的西瓜样本的数据。
特征(feature)/属性(attribute):反应事件或对象在某方面的表现或性质。在此数据中,色泽、根蒂、敲声 这三项就是本数据中的特征。
属性值(attribute value):属性值就是指数据中特征的具体描述。例如本数据中的色泽特征下的属性值就是 青绿、乌黑等关于色泽的描述,也就是色泽的取值。
样本空间(sample space):数据中所有特征组成的空间,称为样本空间。本例中的样本空间就是由三个特征值组成的一个三维空间。每一条数据都可以通过三个特征找到自己在样本空间的位置。
特征向量(feature vector):数据集中的每一样本,在样本空间中都会变成一一对应的向量,所以我们也称一个样本为一个特征向量。
分类:预测的结果是离散的。为了把数据区分出不同的种类。例如区分好瓜,坏瓜。
回归:预测的结果是连续的。为了预测数据对应某种特征的程度。例如判断西瓜的成熟度0.85,0.37。
聚类(clustering): 将训练集中的数据分成若干组,每个组可以称为一个“簇”,这些自动形成的簇可能对应一些潜在的概念划分。这些潜在的划分概念我们是不知道的。
监督学习(supervised learning):通过学习已知的数据得到一个模型,该模型可以预测相同数据的对应结果。分类和回归均属于监督学习。
无监督学习(unsupervised learning):为获得潜在的未知的属性值,对数据集进行学习。聚类为无监督学习的代表。
1.3假设空间
归纳:从特殊到一般的“泛化”过程,即从具体的事实归结出一般性的规律。
演绎:从一般到特殊的“特化”过程,即从基础原理推演出具体状况。
机器学习中,大多是完成归纳任务,所以我们可以将训练过程称为“归纳学习”
我们可以把学习过程看作一个在所有假设组成的空间中进行搜索的过程。假设的表示一旦确定,假设空间及其规模大小就确定了。
西瓜例子中的空间假设:
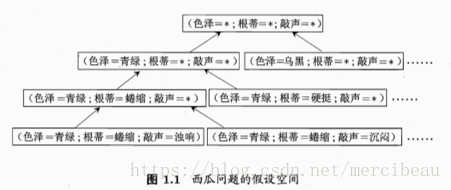
西瓜数据集中存在三个特征色泽,根蒂,敲声。每个特征拥有3个可能的属性值。但是有可能某个特征并不会影响好瓜坏瓜的结果。所以一个西瓜的结果最终会由每个特征的某个确定属性值和忽略这个特征来决定。所以每个特征的三个属性值和忽略这个特征就是我们所有假设。下面我们对一个瓜的结果作假设,那么假设空间的大小就是(3+1)*(3+1)*(3+1) = 64。但是有可能好瓜这个概念根本不存在,没有好瓜这个东西。所以要额外添加一个假设。那么最终的假设空间就是 64 + 1 = 65.
1.4 归纳偏好
机器学习算法在学习过程中对某种类型假设的偏好,称为“归纳偏好”。算法的偏好可以是选择“尽可能一般”的模型,也可以是选择“尽可能特殊的模型”。
任何一个有效的机器学习算法必有其归纳偏好。
奥卡姆剃刀定律:若有多个假设与观察一致,则选择最简单的哪个。
NFL(没有免费的午餐):要谈论算法的相对优劣,必须要针对具体的学习问题。
习题
1.1
| 编号 | 色泽 | 根蒂 | 敲声 | 好瓜 |
| 1 | 青绿 | 卷缩 | 浊响 | 是 |
| 4 | 乌黑 | 稍卷 | 沉闷 | 否 |
根据之前的知识,两个数据中,有一个好瓜,得到一组好瓜数据,根据这组数据我们来推算一个瓜每个的特征取何值时,才能是一个好瓜呢。对于色泽来说,可能的取值为青绿或者无关,根蒂的取值为卷缩或者无关,敲声的取值为浊响或者无关。所以组成的版本空间为2*2*2=8.但是我们知道了乌黑、稍卷、沉闷的瓜不是好瓜。所以之前的8个假设中我们要除去,无关、无关、无关这一条。所以最终这个两条数据组成的版本空间为。
| 1 | 青绿 | 卷缩 | 浊响 |
| 2 | 青绿 | 卷缩 | 无关(任意) |
| 3 | 青绿 | 无关(任意) | 浊响 |
| 4 | 青绿 | 无关(任意) | 无关(任意) |
| 5 | 无关(任意) | 卷缩 | 浊响 |
| 6 | 无关(任意) | 卷缩 | 无关(任意) |
| 7 | 无关(任意) | 无关(任意) | 浊响 |
1.2
| 编号 | 色泽 | 根蒂 | 敲声 | 好瓜 |
| 1 | 青绿 | 卷缩 | 浊响 | 是 |
| 2 | 乌黑 | 卷缩 | 浊响 | 是 |
| 2 | 青绿 | 硬挺 | 清脆 | 否 |
| 4 | 乌黑 | 稍卷 | 沉闷 | 否 |
首先我们先找出所有的假设空间,色泽特征3个取值(青绿、乌黑、任意),根蒂特征4个取值(卷缩、硬挺、稍卷、任意),敲声特征4个取值(浊响、清脆、沉闷、任意)。所以假设空间的大小为 3 * 4 * 4 + 1 = 49.最后的 + 1 是不存在好瓜这个假设。
因为任意可以替代某项特征中的具体取值,所以我们我们需要去除冗余项,即不带任意的假设。共有 2 * 3 * 3 = 18个。所以不冗余的假设空间拥有 18条假设。
所以 k <= 18。
当 k = 1 时,拥有全部48种可能性。
当 k = 2 时,拥有48 * 47 / 2= 1128 - (47 +(2*15+6*11) + (2*9 + 6*6))= 931种可能。
当 k = 3 时,拥有 48*47*46/2*3=17296-(冗余项)
。
。
。
当 k = 18 时,拥有 3*3
代码主要就是先完成所有排列组合,然后删除冗余项。代码很蠢但是还可以运行。
但是结果与
https://blog.csdn.net/icefire_tyh/article/details/52065626
这位高手的结果有区别,除了1,2与他相同,之后的总是比他多一些。
k = 5 , 346712
k = 4 , 72647
k = 3 , 10341
k = 2 , 931
k = 1 , 48
程序太笨只跑到k=5的值。
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import itertools
feature1 = [0,1,2]
feature2 = [0,1,2,3]
feature3 = [0,1,2,3]
equations = []
for a in range(3):
first = feature1[a]
for b in range(4):
second = feature2[b]
for c in range(4):
third = feature3[c]
equation = str(first) + str(second) + str(third)
equations.append(equation)
res = []
ress = res*2
def find(k,equations):
list = [c for c in itertools.combinations(equations,k)]
equa = [0]*len(list)
for i in range(len(list)):
item = list[i]
for j in range(len(item)):
a = str(item[j])
for h in range(len(item)):
if h == j:
continue
b = str(item[h])
#print(a,b,item)
#一个特征冗余
if a[0] == b[0] and a[1] == b[1] and a[0] != '0' and a[1] != '0' and b[2] != '0' and a[2] == '0':
equa[i] = 1
if a[0] == b[0] and a[2] == b[2] and a[0] != '0' and a[2] != '0' and b[1] != '0' and a[1] == '0':
equa[i] = 1
if a[1] == b[1] and a[2] == b[2] and a[1] != '0' and a[2] != '0' and b[0] != '0' and a[0] == '0':
equa[i] = 1
#两个特征冗余
if a[0] == b[0] and a[0] != '0' and a[1] == '0' and a[2] == '0':
equa[i] = 1
if a[1] == b[1] and a[1] != '0' and a[0] == '0' and a[2] == '0':
equa[i] = 1
if a[2] == b[2] and a[2] != '0' and a[0] == '0' and a[1] == '0':
equa[i] = 1
# 三个特征冗余
if a[0] == '0' and a[1] == '0' and a[2] == '0':
equa[i] = 1
#print('3', a, b)
num = 0
for i in range(len(equa)):
if equa[i] == 0:
num += 1
print(list[i])
k -= 1
print(num)
if k > 0:
return find(k, equations)
else:
return len(res)
find(6, equations)
1.3
当假设空间存在不能满足所有训练样本的时候,我的倾向是选择挑选出好瓜更严格的假设空间,因为考虑到实际情况,既然来挑选西瓜了,所以肯定更倾向于挑出好瓜,所以我认为在挑选假设空间的时候,可以根据“尽可能严格”作为归纳偏好。
最后
以上就是朴实滑板最近收集整理的关于机器学习(周志华)读书笔记+课后习题 第一章的全部内容,更多相关机器学习(周志华)读书笔记+课后习题内容请搜索靠谱客的其他文章。








发表评论 取消回复