1. 首页
  2. 文章中心
  3. c++

Codeforces Round #532 (Div. 2) 题解碎碎念A Roman and BrowserB Build a ContestC NN and the Optical IllusionD Dasha and ChessE Andrew and TaxiCF1100F Ivan and Burgers

96 阅读 0 评论
我是靠谱客的博主 害羞鱼，最近开发中收集的这篇文章主要介绍Codeforces Round #532 (Div. 2) 题解碎碎念A Roman and BrowserB Build a ContestC NN and the Optical IllusionD Dasha and ChessE Andrew and TaxiCF1100F Ivan and Burgers，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

碎碎念

最近好颓啊，bzoj权限到期，cf又没时间打，还要忙着快乐文化课。。

翻译来自洛谷

A Roman and Browser

给定一个长度为 n n n的只有 1 1 1和 − 1 −1 −1的序列，选择一个位置 b b b，然后删掉位置为 b + i × k b+itimes k b+i×k的数（ i i i为整数），求操作后 1 1 1和 − 1 −1 −1数量的最大绝对差值

没啥好说的，常规A题难度，直接模拟即可

#include <stdio.h>
#include <string.h>
#include <algorithm>
#define rep(i,st,ed) for (int i=st;i<=ed;++i)

const int N=20005;

int a[N];

int main(void) {
	int n,k,sum=0,mx=0; scanf("%d%d",&n,&k);
	rep(i,1,n) scanf("%d",&a[i]),sum+=a[i];
	rep(i,1,k) {
		int s=sum;
		for (int j=i;j<=n;j+=k) s-=a[j];
		mx=std:: max(mx,abs(s));
	}
	printf("%dn",mx);
	return 0;
}

B Build a Contest

有 n n n个题，每个题有一个难度 a i ( 1 ≤ a i ≤ m ) a_i(1le a_ile m) ai​(1≤ai​≤m)，从左往右加入题，当加入的题中 m m m个难度都出现时，输出 1 1 1并把每个难度都删除一道题，否则输出 0 0 0，求输出序列

我们线段树单点修改+查询全局最小值，实在无脑直接再上一个区间减即可

#include <stdio.h>
#include <string.h>
#include <algorithm>
#define rep(i,st,ed) for (int i=st;i<=ed;++i)

const int N=200005;

int s[N<<2];

int read() {
	int x=0,v=1; char ch=getchar();
	for (;ch<'0'||ch>'9';v=(ch=='-')?(-1):(v),ch=getchar());
	for (;ch<='9'&&ch>='0';x=x*10+ch-'0',ch=getchar());
	return x*v;
}

void mdf(int x,int l,int r,int v) {
	if (v<l||v>r) return ;
	if (l==r) return (void) (s[x]++);
	int md=(l+r)>>1;
	mdf(x<<1,l,md,v); mdf(x<<1|1,md+1,r,v);
	s[x]=std:: min(s[x<<1],s[x<<1|1]);
}

int main(void) {
	int m=read(),n=read(),rec=1;
	rep(i,1,n) {
		int x=read();
		mdf(1,1,m,x);
		if (s[1]>=rec) {
			putchar('1');
			rec++;
		} else putchar('0');
	}
	return 0;
}

C NN and the Optical Illusion

有一个圆，在其周围摆一圈圆，如图所示：
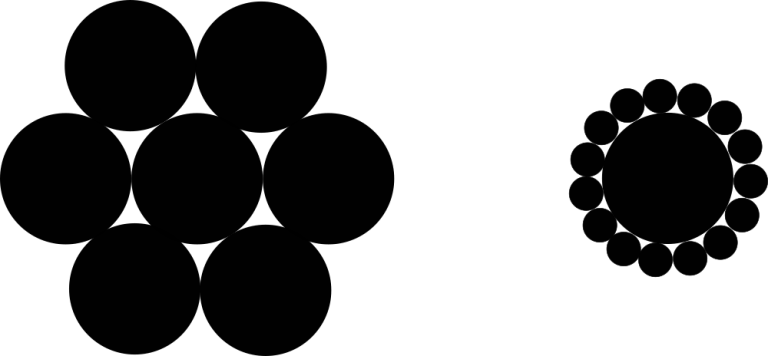
在这里插入图片描述
现已知内圆半径 r r r，和外圆个数 n n n，你要求出外圆半径 R R R。
假设你输出的答案是 a a a，标准答案为 b b b，如果 ∣ a − b ∣ max ⁡ ( 1 , b ) ≤ 1 0 − 6 frac{|a-b|}{max(1,b)}le10^{-6} max(1,b)∣a−b∣​≤10−6，你的答案被算作正确。

高中生数学题。n个圆恰好组成正n边形，我们随便抽一个等腰三角形出来求出顶角，用正弦定理然后化一下柿子就可以了。
R = r s i n α 2 1 − s i n α 2 R=frac{rsinfrac{alpha}{2}}{1-sinfrac{alpha}{2}} R=1−sin2α​rsin2α​​
其中r是内圆半径，R是外圆半径

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <math.h>

const double pi=acos(-1);

int main(void) {
	int n,r; scanf("%d%d",&n,&r);
	double arc=2.0*pi/n;
	double sn=sin(arc*0.5);
	printf("%.7lfn", r*sn/(1-sn));
}

D Dasha and Chess

999 × 999 999×999 999×999的棋盘上，有一个白王和 666 666 666个黑车，每次白王可以往 8 8 8个方向走一格，黑车可以随便移动到某个没有棋子的位置，当黑车移动后白王和某个黑车在同一行/列时白王赢，求白王在 2000 2000 2000步之内的必胜策略

脑洞是好东西，我也想要一个
我们首先走到最中间 ( 500 , 500 ) (500,500) (500,500)，最坏的情况为四个角落分别有(166,166,167,167)个车，我们只需要向着车最多的角落走斜线就可以了
至于正确性，我们从 ( 500 , 500 ) (500,500) (500,500)到任意角落只需要 499 499 499步，而角落车的数量至少有 166 + 167 + 167 = 500 166+167+167=500 166+167+167=500只。
实现的时候注意只能走空格。。

嘴巴AC没有代码

E Andrew and Taxi

给定一个有向图，改变其中某些边的方向，它将成为一个有向无环图。
现在求一个改变边方向的方案，使得所选边边权的最大值最小。

首先答案肯定是单调的。考虑二分答案mid，我们把大于mid的边都加图里判环，若出现环了肯定不可行
考虑没有环的情况。我们对新图做拓扑排序，需要修改的边一定是逆着拓扑序连接的。我们把这些边反向就可以惹

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <vector>
#define rep(i,st,ed) for (register int i=st;i<=ed;++i)
#define fill(x,t) memset(x,t,sizeof(x))

const int N=200005;

struct edge {int x,y,w,next;} e[N],g[N];

std:: vector <int> ans;

int ls[N],d[N],edCnt;
int q[N],p[N];

int read() {
	int x=0,v=1; char ch=getchar();
	for (;ch<'0'||ch>'9';v=(ch=='-')?(-1):(v),ch=getchar());
	for (;ch<='9'&&ch>='0';x=x*10+ch-'0',ch=getchar());
	return x*v;
}

void add_edge(int x,int y,int w) {
	e[++edCnt]=(edge) {x,y,w,ls[x]}; d[y]++; ls[x]=edCnt;
}

bool cmp(edge a,edge b) {
	return a.w<b.w;
}

bool top_sort(int n) {
	int h=1,t=0;
	rep(i,1,n) if (!d[i]) q[++t]=i;
	for (;h<=t;) {
		int x=q[h++]; p[x]=h-1;
		for (int i=ls[x];i;i=e[i].next) {
			if (!(--d[e[i].y])) {
				q[++t]=e[i].y;
			}
		}
	}
	return t==n;
}

bool check(int mid,int n,int m) {
	rep(i,0,n) d[i]=ls[i]=0; edCnt=0;
	rep(i,mid+1,m) add_edge(g[i].x,g[i].y,g[i].y);
	return top_sort(n);
}

int main(void) {
	freopen("data.in","r",stdin);
	int n=read(),m=read();
	rep(i,1,m) {
		int x=read(),y=read(),w=read();
		g[i]=(edge) {x,y,w,i};
	}
	std:: sort(g+1,g+m+1,cmp);
	if (check(0,n,m)) {
		puts("0 0");
		return 0;
	}
	int l=1,r=m;
	for (;l<=r;) {
		int mid=(l+r)>>1;
		if (check(mid,n,m)) {
			r=mid-1; ans.clear();
			rep(i,1,mid) if (p[g[i].x]>p[g[i].y]) {
				ans.push_back(g[i].next);
			}
		}
		else l=mid+1;
	}
	printf("%d %dn", g[r+1].w,(int)ans.size());
	for (int i=0;i<ans.size();++i) printf("%d ", ans[i]); puts("");
	return 0;
}

CF1100F Ivan and Burgers

给定 n n n和 a i … n a_{idots n} ai…n​
有 q q q个询问：
给定 l , r l,r l,r
求在 a l … r a_{ldots r} al…r​​中选取任意个，使得他们的异或和最大。

很容易想到线性基求异或最大值，区间问题自然想到套在线段树上解决，可惜这样是 O ( n l o g 3 n ) O(nlog^3n) O(nlog3n)的
我们离线做。对于跨过mid的询问，维护从mid开始的前缀和后缀线性基，然后合并查询就可以了。对于不跨过的分治即可
分析一下复杂度是 O ( ( n + q ) l o g 2 n ) O((n+q)log^2n) O((n+q)log2n)的，区别在于只有枚举q时合并了线性基，其余时间都只有插入的操作。
实际上还是可以做到一个log的，具体可以看洛谷的题解

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <vector>
#define rep(i,st,ed) for (register int i=st;i<=ed;++i)
#define drp(i,st,ed) for (register int i=st;i>=ed;--i)
#define fill(x,t) memset(x,t,sizeof(x))

const int N=500005;

struct Gay {
	int r[21],size;
	Gay() { fill(r,0),size=0;}
	void clr() { fill(r,0),size=0;}
	void ins(int x) {
		drp(i,19,0) if ((x>>i)&1) {
			if (!r[i]) {
				size++; r[i]=x;
				return ;
			} else x^=r[i];
		}
	}
	int get_max() {
		int res=0;
		drp(i,19,0) if ((res^r[i])>res) res^=r[i];
		return res;
	}
} G[N<<2],wjp;

struct Q {int l,r,id;} q[N];

int ans[N],a[N];

int read() {
	int x=0,v=1; char ch=getchar();
	for (;ch<'0'||ch>'9';v=(ch=='-')?(-1):(v),ch=getchar());
	for (;ch<='9'&&ch>='0';x=x*10+ch-'0',ch=getchar());
	return x*v;
}

void solve(int l,int r,int L,int R) {
	if (R<L) return ;
	int mid=(l+r)>>1;
	G[mid].clr(); G[mid].ins(a[mid]);
	rep(i,mid+1,r) {
		G[i]=G[i-1];
		G[i].ins(a[i]);
	}
	drp(i,mid-1,l) {
		G[i]=G[i+1];
		G[i].ins(a[i]);
	}
	std:: vector <Q> v1,v2;
	rep(i,L,R) if (q[i].r<mid) v1.push_back(q[i]);
	else if (q[i].l>mid) v2.push_back(q[i]);
	else {
		wjp=G[q[i].l];
		rep(j,0,19) wjp.ins(G[q[i].r].r[j]);
		ans[q[i].id]=wjp.get_max();
	}
	int cnt=0,rec;
	for (int i=0;i<v1.size();++i) q[L+cnt++]=v1[i];
	rec=L+cnt;
	for (int i=0;i<v2.size();++i) q[L+cnt++]=v2[i];
	solve(l,mid,L,rec-1);
	solve(mid+1,r,rec,L+cnt-1);
}

int main(void) {
	freopen("data.in","r",stdin);
	freopen("myp.out","w",stdout);
	int n=read();
	rep(i,1,n) a[i]=read();
	int T=read();
	rep(i,1,T) q[i].l=read(),q[i].r=read(),q[i].id=i;
	solve(1,n,1,T);
	rep(i,1,T) printf("%dn", ans[i]);
	return 0;
}

然后就完了。

最后

以上就是害羞鱼为你收集整理的Codeforces Round #532 (Div. 2) 题解碎碎念A Roman and BrowserB Build a ContestC NN and the Optical IllusionD Dasha and ChessE Andrew and TaxiCF1100F Ivan and Burgers的全部内容，希望文章能够帮你解决Codeforces Round #532 (Div. 2) 题解碎碎念A Roman and BrowserB Build a ContestC NN and the Optical IllusionD Dasha and ChessE Andrew and TaxiCF1100F Ivan and Burgers所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(64)

相关文章

解决codeforces访问慢的问题
解决codeforces访问慢的问题
Codeforces Round #541 (Div. 2) 题解
Codeforces Round #541 (Div. 2) 题解
CodeForces - 1368B Codeforces Subsequences（思维）
CodeForces - 1368B Codeforces Subsequences（思维）
E. Andrew and Taxi（二分+拓扑判环）
E. Andrew and Taxi（二分+拓扑判环）
Codeforces Round #532 (Div. 2) 题解碎碎念A Roman and BrowserB Build a ContestC NN and the Optical IllusionD Dasha and ChessE Andrew and TaxiCF1100F Ivan and Burgers
Codeforces Round #532 (Div. 2) 题解碎碎念A Roman and BrowserB Build a ContestC NN and the Optical IllusionD Dasha and ChessE Andrew and TaxiCF1100F Ivan and Burgers
【codeforces】Educational Codeforces Round 141 [Rated for Div. 2]AB题解
【codeforces】Educational Codeforces Round 141 [Rated for Div. 2]AB题解
Codeforces 1249C2 Good Numbers (hard version)思路：代码：
Codeforces 1249C2 Good Numbers (hard version)思路：代码：
Codeforces 1323B
Codeforces 1323B

评论列表共有 0 条评论

立即
投稿
返回
顶部