CodeForces - 1463E Plan of Lectures(拓扑排序+并查集缩点)

83 阅读 0 评论 55 点赞

我是靠谱客的博主尊敬唇膏，最近开发中收集的这篇文章主要介绍CodeForces - 1463E Plan of Lectures(拓扑排序+并查集缩点)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目链接：点击查看

题目大意：给出一棵有根树，树边都是有向边，再给出 $k$ 个关系 $(x, y)$ ，其意义是访问完点 $x$ 后需要立即访问点 $y$ ，问是否存在一种合适的拓扑序

题目分析：因为题目说明了 $k$ 个关系实际上也是一种绑定关系，在访问点 $x$ 后需要立即访问点 $y$ ，所以不妨直接将点 $y$ 与点 $x$ 合并在一起，更具体的说，可以将 $x$ 和 $y$ 进行缩点，然后对缩点后的图进行拓扑，稍微画一下样例的图就能明白了：
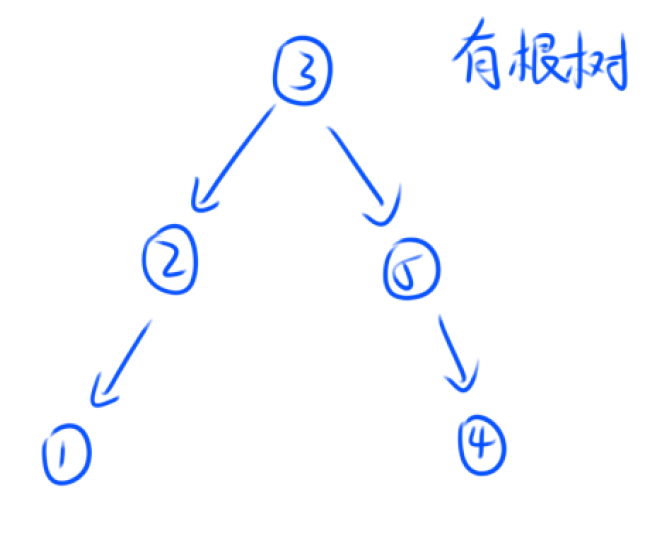
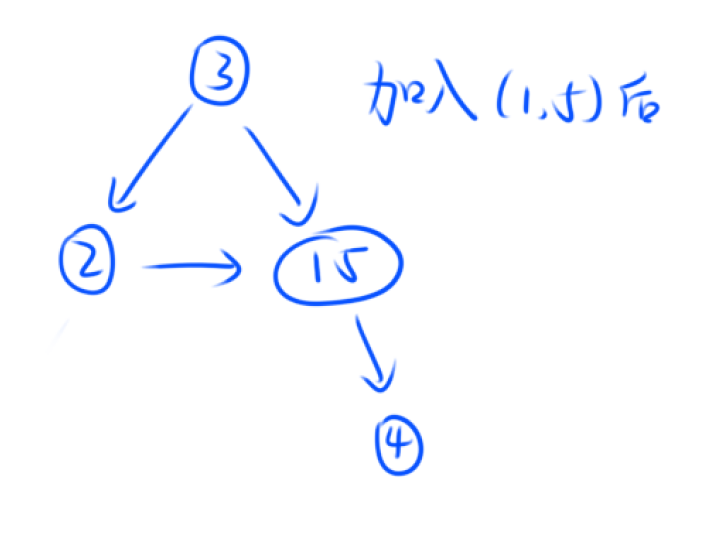
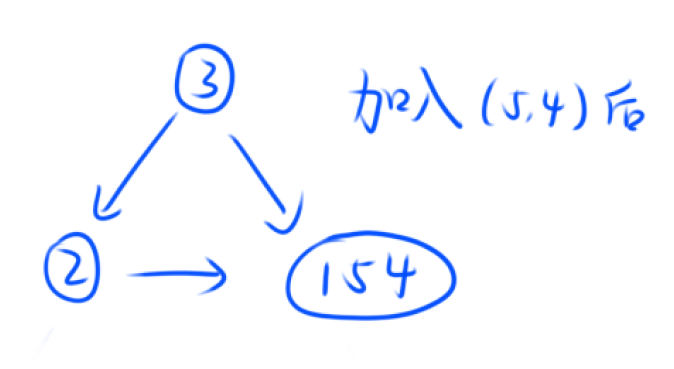
在这里插入图片描述

剩下的注意一下细节直接实现就可以了，需要注意的是， $k$ 个关系可能会组成环，这些都是需要特判的

代码：

// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast","inline","-ffast-math")
// #pragma GCC target("avx,sse2,sse3,sse4,mmx")
#include<iostream>
#include<cstdio>
#include<string>
#include<ctime>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<stack>
#include<climits>
#include<queue>
#include<map>
#include<set>
#include<sstream>
#include<cassert>
#include<bitset>
#include<unordered_map>
using namespace std;

typedef long long LL;

typedef unsigned long long ull;

const int inf=0x3f3f3f3f;

const int N=1e6+100;

int p[N],f[N],nt[N],c[N],ord[N],ban[N],du[N],id;

vector<int>node[N],dcc[N],ans;

int find(int x)
{
	return f[x]==x?x:f[x]=find(f[x]);
}

void merge(int x,int y)//y->x
{
	int xx=find(x),yy=find(y);
	if(xx!=yy)
		f[yy]=xx;
}

int topo(int st)
{
	int cnt=0;
	queue<int>q;
	q.push(st);
	while(q.size())
	{
		int u=q.front();
		q.pop();
		cnt++;
		for(auto it:dcc[u])
			ans.push_back(it);
		for(auto v:node[u])
			if(--du[v]==0)
				q.push(v);
	}
	return cnt;
}

int main()
{
#ifndef ONLINE_JUDGE
//  freopen("data.in.txt","r",stdin);
//  freopen("data.out.txt","w",stdout);
#endif
//  ios::sync_with_stdio(false);
	int n,m,rt;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",p+i);
		if(p[i]==0)
			rt=i;
	}
	for(int i=1;i<=m;i++)//并查集缩点
	{
		int u,v;
		scanf("%d%d",&u,&v);
		nt[u]=v;
		ban[v]=true;//v被缩到u的集合中去，在新图中相当于被ban掉了
		merge(u,v);
	}
	for(int i=1;i<=n;i++)//缩点
	{
		if(ban[i])
			continue;
		id++;
		int pos=i;
		while(pos&&!c[pos])//注意这里会出现环的情况
		{
			ord[pos]=dcc[id].size();
			dcc[id].push_back(pos);
			c[pos]=id;
			pos=nt[pos];
		}
	}
	for(int i=1;i<=n;i++)//如果拓扑存在环的话，就不会被遍历到
		if(!c[i])
			return 0*puts("0");
	for(int i=1;i<=n;i++)//建边
	{
		if(i==rt)
			continue;
		if(c[i]!=c[p[i]])
		{
			node[c[p[i]]].push_back(c[i]);
			du[c[i]]++;
		}
		else if(ord[p[i]]>ord[i])//特判
			return 0*puts("0");
	}
	if(topo(c[rt])!=id)//拓扑中有环
		return 0*puts("0");
	for(auto it:ans)
		printf("%d ",it);
	puts("");
    return 0;
}