想着趁着疫情在家，安心学习一下。加入了Datawhale的公益课程“14天挑战《动手学深度学习》（Pytorch版）”，李沐大神的书早就买了，可是MXNet一直让我望而却步，刚好有这次机会学习Pytorch版的，何乐而不为呢？

刚好需要打卡，便写系列博客用于记录学习过程中的一些想法及笔记吧。
第一天，当然就是机器学习的“Hello World”了——线性回归

本节对应《动手学深度学习》第3章3.1-3.3节
环境为 Pytorch 1.2.0，Python 3.7

原书地址：
http://zh.d2l.ai/chapter_deep-learning-basics/linear-regression.html
pytorch版代码地址：
https://github.com/ShusenTang/Dive-into-DL-PyTorch/tree/master/code/chapter03_DL-basics

基本介绍

线性回归输出连续值，适用于回归问题。关于其介绍，书上以及网上都有很多讲解，而馆长经过反反复复断断续续地学习机器学习，翻过的书前面基本都是线性回归，所以这次学习没什么压力，主要是梳理几个公式。

基本模型

例如预测房价问题，假设只有两个变量，房屋面积$x_1$，房龄$x_2$，售出价格为$y$，线性回归就是通过构造输入与假设输出$\hat{y}$之间的线性关系，来预测输出。
$$\hat{y}=x_1{w}_1+x_2{w}_2+b$$

其中式子的参数为权重$w$和偏差$b$，假设只有一个变量的话，那就是中学非常熟悉的直线方程了$y=ax+b$，参数为斜率与截距，当然这也是单变量线性回归的表达值。
如果扩展到更多的变量，当然不可能一一写出来了，这时就需要用到线性代数的表达形式：
$$\hat{y}=WX+b$$

至于权重与变量到底是谁乘以谁，$WX$还是$XW$，其实主要是看自己的数据维度，馆长在学习神经网络时，常常被这些谁乘谁这个问题搞烦，后来干脆每次都拿出纸笔，根据维度来计算，得到下一层需要的输入维度，吴恩达在机器学习课程上也这么推荐了，这有助于减少程序中因维度问题而可能出现的bug。

模型训练

有了模型，则需要进行训练。训练的目的就是为了让你的某个标准提高，例如预测准确率，而为了衡量预测结果与真实结果又需要一个指标，这就是损失函数(loss function)。损失函数有许多，在线性回归中常使用平方误差损失函数：
$${\ell }^{(i)}(w_1,w_2,b)=\frac{1}{2}{\left({\hat{y}}^{(i)}-y^{(i)}\right)}^2$$

式子除以了2，主要是为了平方求导时更加方便。这个式子针对的是第$i$个样本，对于全部要本则需要把所有的误差加起来：
$$\ell (w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n{\ell }^{(i)}(w_1,w_2,b)$$

训练就是希望找到一组参数，使得损失函数最小，从而预测最准确。
$$\underset{w_1,w_2,b}{\mathrm{argmin}}\ell (w_1,w_2,b)$$

如何找到这一组参数呢？前面说到了为了求导方便，所以实际上这个问题是可以利用数学方法来求解析解的，如果对矩阵微分等内容较为了解，多变量线性回归解析解为（这里的$\Theta$实际上包括了偏差，在此不做详细说明）
$$\Theta =(X^{T}X{)}^{-1}{X}^{T}y$$

然而，并不是每一个问题都可以得到解析解，而且特征过多时，求解析解的计算消耗很大，应该需要一些更加普适的方法。这就是优化算法。

通过优化算法有限次迭代模型参数来尽可能降低损失函数的值，得到的解就是数值解。

书中使用了小批量随机梯度下降（mini-batch stochastic gradient descent）。
……（后续理论懒得写了，直接上代码）

线性回归从零实现

为了理解深度学习工作原理，书中大部分的案例都给出了从零实现，再给出MXNET的实现（这里是Pytorch）。对于线性回归这种简单的案例，还是需要透彻理解的。

生成数据集

这里构造了一个1000个训练样本，特征数为2的训练集，即（1000,2），噪声服从均值为0，标准差为0.01的正太分布，结合权重和偏置如下：

$$y=2x_1-3.4x_2+4.2+ϵ$$

建议在生成数据集时，都定义好dtype，以防有时出问题。

num_inputs = 2
num_examples = 1000

true_w = [2, -3.4]
true_b = 4.2

features = torch.randn(num_examples, num_input, dtype=torch.float32) # [1000, 2]
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32)

在每一次运算时，应该理解清楚数据的格式，行列关系，尤其是以后处理很多特征时。例如此处：features的每⼀⾏是⼀个⻓度为2的向量， 而labels的每⼀⾏是⼀个⻓度为1的向量 。

读取数据

定义函数，每次返回batch_size个随机样本的特征和标签，这个函数保存在前面链接github中的d2lzh_pytorch。

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices) # random read 10 samples
    for i in range(0, num_examples, batch_size):
        # the last time may be not enough for a whole batch
        # 最后一个batch 如果大于num_examples1000，取1000
        j = torch.LongTensor(indices[i: min(i+batch_size, num_examples)])
        yield features.index_select(0, j), labels.index_select(0, j)

添加了yield的函数相当生成器，关于它的理解可以看这篇博客：

python中yield的用法详解——最简单，最清晰的解释: https://blog.csdn.net/mieleizhi0522/article/details/82142856

不妨尝试使用data_iter来读取一下数据样例，可以得到（10,2）的X和（10,1）的y

# 读取一组10个X，y
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, 'n', y)
    break

tensor([[ 0.8900,  0.6786],
        [ 1.2820,  1.0451],
        [ 1.3100, -1.5853],
        [ 0.0556, -0.1727],
        [-0.3048,  0.0427],
        [-0.1345,  0.7214],
        [-0.7889,  0.0265],
        [ 0.2193,  0.4227],
        [-0.5117,  0.2417],
        [ 0.7750, -1.6158]]) 
 tensor([ 3.6749,  3.2164, 12.1911,  4.8974,  3.4356,  1.4775,  2.5383,  3.1946,
         2.3714, 11.2563])

初始化模型参数

在这里初始化$w,b$的参数，权重服从均值为0，方差0.01的正态分布，维度为（2,1），偏差则设为1。
至于为什么需要这么初始化模型参数，可参考书中章节3.15关于数值稳定性和模型初始化的相关内容。主要是为了防止权重衰减和爆炸，如果设置成相同的值则各单元输入相同，具体可看：

《动手学深度学习》3.15. 数值稳定性和模型初始化
http://zh.d2l.ai/chapter_deep-learning-basics/numerical-stability-and-init.html

定义模型

做好准备后就需要定义模型，这里使用torch.mm来进行矩阵运算
$$\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}=w_{\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}}\cdot \mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}+w_{\mathrm{a}\mathrm{g}\mathrm{e}}\cdot \mathrm{a}\mathrm{g}\mathrm{e}+b$$
不妨看一看输出维度：
$$Xw->(1000,2)\times (2,1)=(1000,1)+b(1)->\hat{y}=(1000,1)$$

def linreg(X, w, b):
    return torch.mm(X, w) + b

X与w相乘后得到了一个1000行1列的列向量，再加上b，这里使用了广播机制，将b从1维变成了（1000,1）从而完成运算，得到预测的结果，也是（1000,1）。

虽然这里运算很简单，一眼就可以看出来，但和前面所说一样，要学会使用数学方法来防止bug，避免以后很多特征可能出现的错误。

定义损失函数

将前面介绍的均方误差损失函数用代码实现
$$l^{(i)}(\mathbf{w},b)=\frac{1}{2}{\left({\hat{y}}^{(i)}-y^{(i)}\right)}^2,$$

def squared_loss(y_hat, y):
    #return (y_hat - y)**2 / 2
    return (y_hat - y.view(y_hat.size())) ** 2 / 2

馆长第一次也想，为什么需要把$y$的形状转化成$\hat{y}$的形状，然后使用了注释掉的那一部分，后来发现不对。
分析一番，原来y_hat的形状是[n,1]的列向量，y的形状是[n]的行向量，如果直接相减，根据广播机制，得到[n,n]，但实际上需要得到的是[n,1]，可以动手试一下：

y_hat = torch.rand(5,1)
y = torch.tensor([1,2,3,4,5], dtype=torch.float)
print(y, y.shape)
print(y_hat, y_hat.shape)
a = squared_loss(y_hat, y) # return (y_hat - y.view(y_hat.size())) ** 2 / 2
b = sl(y_hat, y) # return (y_hat - y)**2 / 2
print(a, a.shape)
print(b, b.shape)

结果如下

所以我们需要把真实值y变形成预测值y_hat的形状，故需要reshape/view

伯禹平台的课后题也有这个问题：

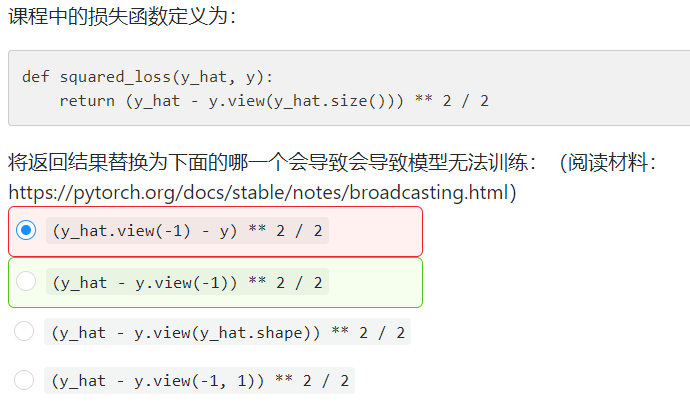
答案解释：
y_hat的形状是[n, 1]，而y的形状是[n]，两者相减得到的结果的形状是[n, n]，相当于用y_hat的每一个元素分别减去y的所有元素，所以无法得到正确的损失值。
对于第一个选项，y_hat.view(-1)的形状是[n]，与y一致，可以相减；
对于第二个选项，y.view(-1)的形状仍是[n]，所以没有解决问题；
对于第三个选项和第四个选项，y.view(y_hat.shape)和y.view(-1, 1)的形状都是[n, 1]，与y_hat一致，可以相减。

定义优化算法

使用随机梯度下降法SGD，函数也在书中配套代码的d2l中，这里写出来

def sgd(params, lr, batch_size):
    # 为了和原书保持一致，这里除以了batch_size，但是应该是不用除的，因为一般用PyTorch计算loss时就默认已经
    # 沿batch维求了平均了。
    for param in params:
        param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data

训练模型

准备好以后就可以开始训练了，首先需要设置超参数：学习率、迭代次数、批量大小，然后定义网络和损失函数

lr = 0.03
num_epochs = 5
batch_size = 10

net = linreg
loss = squared_loss

# training
for epoch in range(num_epochs):
    # in each epoch, all the samples in dataset will be used once
    
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum()
        # calculate the gradient of batch sample loss 
        l.backward()
        # using small batch random gradient descent to iter model parameters
        sgd([w, b], lr, batch_size)
        # reset parameter gradient
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

训练完成后可以发现，得到的权重和偏差与真实的非常接近

w, true_w, b, true_b

至此，线性回归的小案例就已经实现。当然，使用深度学习框架就没这么麻烦了，但是其中的步骤和逻辑大同小异。

线性回归的简洁实现

前面的步骤基本相似

import torch
from torch import nn
import numpy as np
torch.manual_seed(1)

print(torch.__version__)
torch.set_default_tensor_type('torch.FloatTensor')

生成数据集

num_examples = 1000

true_w = [2, -3.4]
true_b = 4.2

features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)

读取数据集

这里使用了pytorch中的DataLoader读取数据，它也是一个可迭代的对象，可以使用多线程并行处理，加快读取数据集的速度，具体可看文档（其实也没写什么）

DataLoader官方文档传送门
https://pytorch.org/docs/stable/torchvision/datasets.html

import torch.utils.data as Data

batch_size = 10

# comebine features and labels of dataset
dataset = Data.TensorDataset(features, labels)

# put dataset into DataLoader
data_iter = Data.DataLoader(
    dataset = dataset, # torch TensorDataset format
    batch_size=batch_size, # mini batch size
    shuffle=True, # wheater shuffle the data 
    num_workers=2, # read data in multithreading
)

定义模型

这里使用Pytorch中定义好了的层，进行一个全连接

net = nn.Sequential(
    nn.Linear(num_inputs, 1)
)

初始化模型参数

分别用正太分布和常量来初始化

nn.init.normal_(net[0].weight, mean=0, std=0.01)
nn.init.constant_(net[0].bias, val=0.0)

定义损失函数和优化函数

这里就体现出框架的便利之处了，直接使用其中预定义的方法

loss = nn.MSELoss()
optimizer = nn.optim.SGD(net.parameters(), lr=0.03)

训练

训练也很简单

num_epochs = 5
for epoch in range(num_epochs):
    for X, y in data_iter:
        output = net(X)
        l = loss(output, y.view(-1, 1))
        optimizer.zero_grad() # reset gradient, equal to net.zero_grad()
        l.backward()
        optimizer.step()
    print('epoch %d, loss: %f' % (epoch, l.item()))

总结

通过这小小的第一步，也算初次了解了Pytorch。总结这次的学习，虽然例子较为简单，但也有不细心可能导致的错误，例如y_hat和y的维度问题。而建立模型基本就是

• 定义模型
• 初始模型参数
• 定义损失函数
• 定义优化器
• 训练

最后，虽然早就想写博客记录一下自己踩过的坑，为其他朋友贡献些力量，无奈数次动笔，都无耐心写下去。此次，才加Pytorch的打卡学习，需要笔记链接来完成打卡，也算是督促自己动动手指吧。如有不足或者错误之处，也欢迎指教。

真菜馆长
2020.2.14 情人节

最后

以上就是笑点低高跟鞋为你收集整理的【动手学深度学习（pytorch版）】笔记1——线性回归基本介绍线性回归从零实现线性回归的简洁实现总结的全部内容，希望文章能够帮你解决【动手学深度学习（pytorch版）】笔记1——线性回归基本介绍线性回归从零实现线性回归的简洁实现总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。