1.给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
leetcode136
def singleNumber(self, nums: List[int]) -> int:
res = 0
for num in nums:
res ^= num
return res
- 异或运算有以下三个性质:
- 任何数和 0 做异或运算,结果仍然是原来的数,即 a ^ 0 = a。
- 任何数和其自身做异或运算,结果是 0,即 a ^ a = 0。
- 异或运算满足交换律和结合律,即 a ^ b ^ a = b ^ a ^ a = b ^ (a ^ a) = b ^ 0 = b。
- 位运算
| 符号 | 运算规则 |
|---|---|
| & | 同为1结果才为1 |
| | | 同为0结果才为0 |
| ^ | 相同为0,不同为1 |
2.使用堆排序方法排序(45,78,57,25,41,89),初始堆为( )
A 78,45,57,25,41,89
B 89,78,57,25,41,45
C 89,78,25,45,41,57
D 89,45,78,41,57,25
- 堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其子结点的值,称为大顶堆;或者每个结点的值都小于或等于其子结点的值,称为小顶堆。
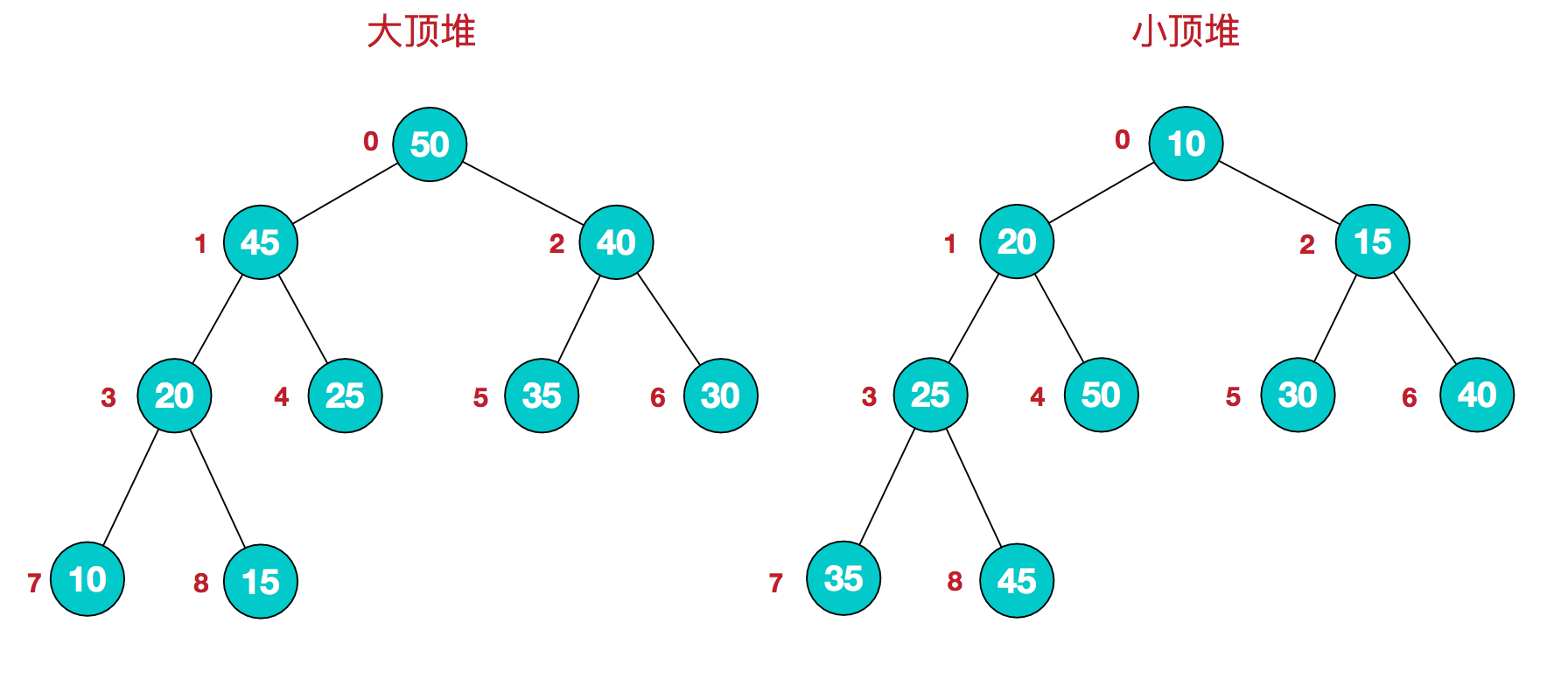
- 对堆中的结点按层进行编号,将其映射到数组中:

- 堆排序的基本思路:
- 将无需序列构建成一个堆,升序采用大顶堆,降序采用小顶堆;
- 将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
- 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,直到整个序列有序。
/**
* 调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上)
* @param arr
* @param i
* @param length
*/
public static void adjustHeap(int []arr,int i,int length){
int temp = arr[i];//先取出当前元素i
for(int k=i*2+1;k<length;k=k*2+1){//从i结点的左子结点开始,也就是2i+1处开始
if(k+1<length && arr[k]<arr[k+1]){//如果左子结点小于右子结点,k指向右子结点
k++;
}
if(arr[k] >temp){//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = temp;//将temp值放到最终的位置
}
答案:B
参考链接:https://www.cnblogs.com/chengxiao/p/6129630.html
3. 回文数:判断一个整数是否是回文数。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
leetcode9
class Solution {
public boolean isPalindrome(int x) {
// 特殊情况:
// 如上所述,当 x < 0 时,x 不是回文数。
// 同样地,如果数字的最后一位是 0,为了使该数字为回文,
// 则其第一位数字也应该是 0
// 只有 0 满足这一属性
if (x < 0 || (x % 10 == 0 && x != 0)) {
return false;
}
int revertedNumber = 0;
// 反转一半数字
while (x > revertedNumber) {
revertedNumber = revertedNumber * 10 + x % 10;
x /= 10;
}
// 当数字长度为奇数时,我们可以通过 revertedNumber/10 去除处于中位的数字。
// 例如,当输入为 12321 时,在 while 循环的末尾我们可以得到 x = 12,revertedNumber = 123,
// 由于处于中位的数字不影响回文(它总是与自己相等),所以我们可以简单地将其去除。
return x == revertedNumber || x == revertedNumber / 10;
}
}
- 整数反转的数学方法:
//pop operation:
pop = x % 10;
x /= 10;
//push operation:
temp = rev * 10 + pop;
rev = temp;
4. 六个圆盘的汉诺塔,总的移动次数是( )
Hanoi(n, a, b):将n个盘子从a柱移到b柱。
f(n):n个盘子的汉诺塔的总移动次数。
- Hanoi(n, a, c) = Hanoi(n-1, a, b) + 1 + Hanoi(n-1, b, c):假设有a、b、c三个柱,要将a上n个盘子移到c,先将a上面n-1个盘子移到b,再将a最下面的盘子移到c,最后将b上的n-1个盘子移到c。
- n盘子汉诺塔问题变成了移动一个盘子 + 两个n-1盘子汉诺塔问题:
f ( n ) = f ( n − 1 ) + 1 + f ( n − 1 ) = 2 f ( n − 1 ) + 1 f ( n ) + 1 = 2 ( f ( n − 1 ) + 1 ) f ( n ) + 1 = 2 ( n − 1 ) ( f ( 1 ) + 1 ) f ( n ) + 1 = 2 n f ( n ) = 2 n − 1 f(n) = f(n-1) + 1 + f(n-1) = 2f(n-1) + 1 \ f(n) + 1 = 2(f(n-1) + 1) \ f(n) + 1 = 2^{(n-1)} (f(1) + 1) \ f(n) + 1 = 2^n \ f(n) = 2^n -1 f(n)=f(n−1)+1+f(n−1)=2f(n−1)+1f(n)+1=2(f(n−1)+1)f(n)+1=2(n−1)(f(1)+1)f(n)+1=2nf(n)=2n−1
答案:2^6 - 1 = 63
5. 设哈希表长度为11,哈希函数为Hash(key)=key%11。存在关键码{47,7,29,11,9,84,54,20,30},采用二次探测法处理冲突,建立的hash表为( )
- 平方探测法:以增量序列 1 2 , − 1 2 , 2 2 , − 2 2 , . . . , q 2 , − q 2 1^2, -1^2, 2^2, -2^2, ... , q^2, -q^2 12,−12,22,−22,...,q2,−q2 且 q<=TableSize/2 循环试探下一个存储地址。
- 一个结论:如果哈希表大小是4k+3的素数(7、11、19),那么只要有空位,就一定能够找的着。
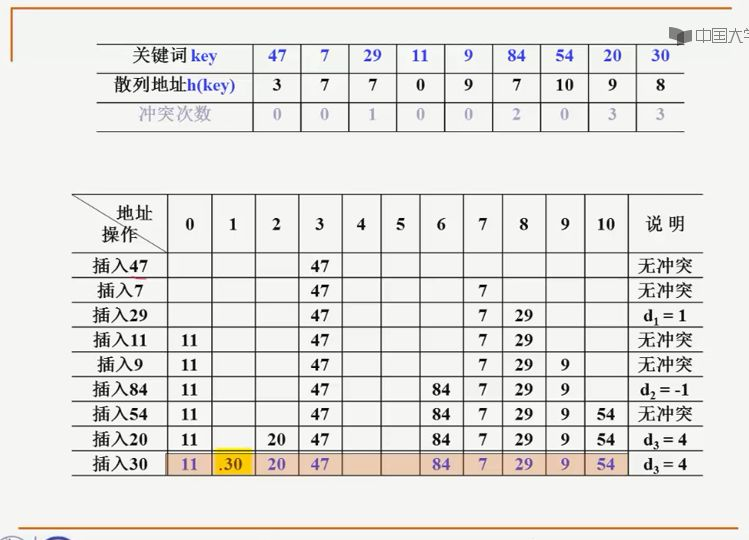
参考地址:https://zhuanlan.zhihu.com/p/34520264
6. 有关希尔排序算法叙述正确的是( )
A.最后一次的步长增量一定为1
B.分割后子序列内部的排序算法是直接插入排序
C.分割后子序列内部的排序算法是直接选择排序
D.希尔排序是稳定排序算法
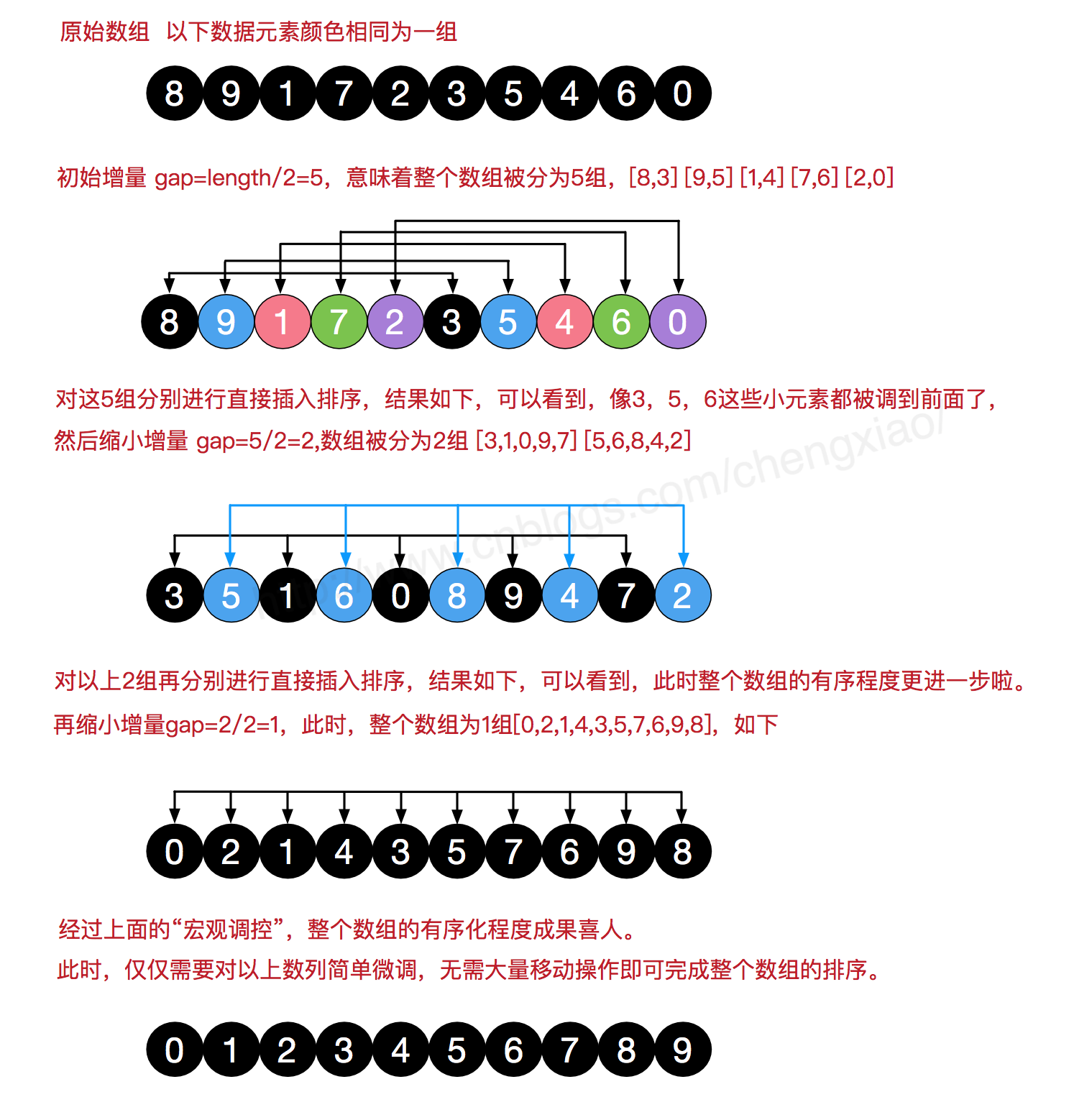
- 希尔排序的步骤:
- 选择增量gap = length/2为起始,以gap = gap/2的方式缩小增量,此增量序列可表示为{n/2, (n/2)/2 , …, 1};
- 通过这个增量将数组元素划分为若干组,分组进行插入排序;
- 然后逐步缩小增量,继续分组进行插入排序,直至增量为1。
/**
* 希尔排序 针对有序序列在插入时采用移动法。
* @param arr
*/
public static void sort1(int []arr){
//增量gap,并逐步缩小增量
for(int gap=arr.length/2;gap>0;gap/=2){
//从第gap个元素,逐个对其所在组进行直接插入排序操作
for(int i=gap;i<arr.length;i++){
int j = i;
int temp = arr[j];
if(arr[j]<arr[j-gap]){
while(j-gap>=0 && temp<arr[j-gap]){
//移动法
arr[j] = arr[j-gap];
j-=gap;
}
arr[j] = temp;
}
}
}
}
正确答案: A B
参考链接:https://www.cnblogs.com/chengxiao/p/6104371.html
最后
以上就是寒冷玉米最近收集整理的关于刷题笔记2020-06-26的全部内容,更多相关刷题笔记2020-06-26内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复