各位高手好！请求PCA与SVD的关系？求解！！！

PCA是得到协方差矩阵的前K个特征向量Uk，然后乘以原数据得到MxK的新数据集以达到降维。我认为：SVD分解之后取前k个奇异值，那么有Vk，原始数据乘以Vk：Data(MxN) X Vk(NxK) = Data(MxK) .这里Vk就是PCA中所求的特征向量。为什么有写书直接拿来Uk或者Vk来计算两条数据的相似度，而不是Data(MxN) X Vk(NxK) = Data(MxK)之后取两行计算相似度呢？已经困惑好几天，求解惑！！！

SVD分解算法及其应用

时间 2013-07-16 11:39:27  十一城

原文  http://elevencitys.com/?p=3923

主题 奇异值分解 算法

矩阵的奇异值分解在矩阵理论的重要性不言而喻，它在最优化问题、特征值问题、最小乘方问题、广义逆矩阵问,统计学,图像压缩等方面都有十分重要的应用。

定义： 设A为m*n阶矩阵， A H A 的n个特征值的非负平方根叫作A的奇异值。记为 σ i (A)。> 如果把A H A的特征值记为λ i (A)，则σ i (A)＝ λ i (A H A)^(1/2)。 

定理 （奇异值分解）设A为m*n阶复矩阵，则存在m阶酉阵U和n阶酉阵V，使得：

A = U*S*V’

其中S=diag(σ i ,σ 2 ,……,σ r )，σ i >0  (i=1,…,r)，r=rank(A) 。 

推论： 设A为m*n阶实矩阵，则存在m阶正交阵U和n阶正交阵V，使得

A = U*S*V’

其中S=diag(σ i ,σ 2 ,……,σ r )，σ i >0  (i=1,…,r)，r=rank(A) 。

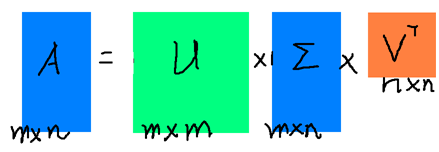
奇异值分解提供了一些关于A的信息，例如非零奇异值的数目（S的阶数）和A的秩相同，一旦秩r确定，那么U的前r 列构成了A的列向量空间的正交基，另外V的从右向左n-r列为A的kernel的基。

非退化的奇异值具有唯一的左、右奇异向量，如果 A 的所有奇异值都是非退化且非零，则它的奇异值分解是唯一的，因为 U 中的一列要乘以一个单位相位因子且同时 V 中相应的列也要乘以同一个相位因子。

根据定义，退化的奇异值具有不唯一的奇异向量。因为，如果 u 1 和 u 2 为奇异值σ的两个左奇异向量，则两个向量的任意规范线性组合也是奇异值σ一个左奇异向量，类似的，右奇异向量也具有相同的性质。因此，如果 MA 具有退化的奇异值，则它的奇异值分解是不唯一的。

在压缩图像应用中，抽象的例子可以入下图所示：

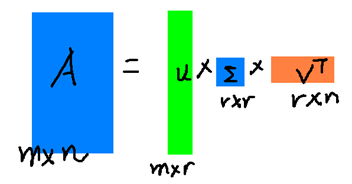
上图中三个矩阵相乘的结果将会是一个接近于A的矩阵，在这儿，r越接近于n，则相乘的结果越接近于A。而这三个矩阵的面积之和（在存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵A，我们如果想要压缩空间来表示原矩阵A，我们存下这里的三个矩阵：U、Σ、V就好了。

主要应用领域

一、奇异值与主成分分析（PCA）

PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量，我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模型的方差很大，那就说明模型不稳定了。但是对于我们用于机器学习的数据（主要是训练数据），方差大才有意义，不然输入的数据都是同一个点，那方差就为0了，这样输入的多个数据就等同于一个数据了。以下面这张图为例子：

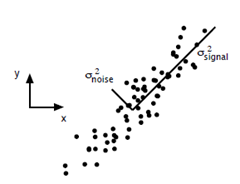
这个假设是一个摄像机采集一个物体运动得到的图片，上面的点表示物体运动的位置，假如我们想要用一条直线去拟合这些点，那我们会选择什么方向的线呢？当然是图上标有signal的那条线。如果我们把这些点单纯的投影到x轴或者y轴上，最后在x轴与y轴上得到的方差是相似的（因为这些点的趋势是在45度左右的方向，所以投影到x轴或者y轴上都是类似的），如果我们使用原来的xy坐标系去看这些点，容易看不出来这些点真正的方向是什么。但是如果我们进行坐标系的变化，横轴变成了signal的方向，纵轴变成了noise的方向，则就很容易发现什么方向的方差大，什么方向的方差小了。

一般来说，方差大的方向是信号的方向，方差小的方向是噪声的方向，我们在数据挖掘中或者数字信号处理中，往往要提高信号与噪声的比例，也就是信噪比。对上图来说，如果我们只保留signal方向的数据，也可以对原数据进行不错的近似了。

PCA的全部工作简单点说，就是对原始的空间中顺序地找一组相互正交的坐标轴，第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的，这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前r个去近似这个空间，这样就从一个N维的空间压缩到r维的空间了，但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。

还是假设我们矩阵每一行表示一个样本，每一列表示一个feature，用矩阵的语言来表示，将一个m * n的矩阵A的进行坐标轴的变化，P就是一个变换的矩阵从一个N维的空间变换到另一个N维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。

而将一个m * n的矩阵A变换成一个m * r的矩阵，这样就会使得本来有n个feature的，变成了有r个feature了（r < n)，这r个其实就是对n个feature的一种提炼，我们就把这个称为feature的压缩。用数学语言表示就是：

但是这个怎么和SVD扯上关系呢？之前谈到，SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子：

在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子

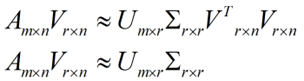
将后面的式子与A * P那个m * n的矩阵变换为m * r的矩阵的式子对照看看，在这里，其实V就是P，也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：

这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U’

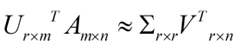
这样我们就得到了对行进行压缩的式子。可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD，那也就实现了PCA了，而且更好的地方是，有了SVD，我们就可以得到两个方向的PCA，如果我们对A’A进行特征值的分解，只能得到一个方向的PCA。

二、奇异值与潜在语义索引LSI

潜在语义索引（Latent Semantic Indexing）与PCA不太一样，至少不是实现了SVD就可以直接用的，不过LSI也是一个严重依赖于SVD的算法，在 矩阵计算与文本处理中的分类问题 中谈到：“三个矩阵有非常清楚的物理含义。

• 第一个矩阵X中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。
• 最后一个矩阵Y中每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。
• 中间的矩阵则表示类词和文章雷之间的相关性。因此，我们只要对关联矩阵A进行一次奇异值分解，w 我们就可以同时完成近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。

下面的例子来自LSA tutorial：

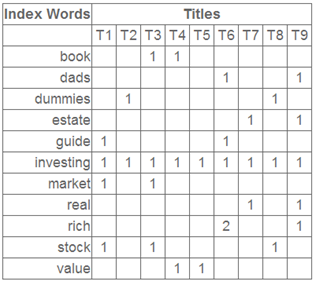
矩阵的一行表示一个词在哪些title中出现了（一行就是之前说的一维feature），一列表示一个title中有哪些词，（这个矩阵其实是我们之前说的那种一行是一个sample的形式的一种转置，这个会使得我们的左右奇异向量的意义产生变化，但是不会影响我们计算的过程）。比如说T1这个title中就有guide、investing、market、stock四个词，各出现了一次，我们将这个矩阵进行SVD，得到下面的矩阵：

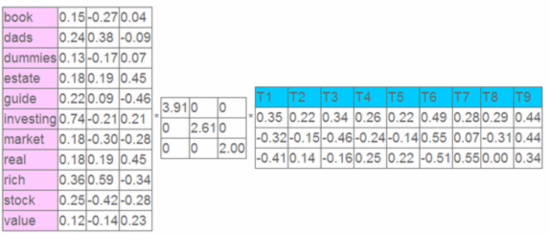
左奇异向量表示“词”的一些特性，右奇异向量表示“文档”的一些特性，中间的奇异值矩阵表示左奇异向量的”一行“与右奇异向量的“一列”的重要程序，数字越大越重要。

另外，左奇异向量的第一列表示每一个词的出现频繁程度，虽然不是线性的，但是可以认为是一个大概的描述，比如book是0.15对应文档中出现的2次，investing是0.74对应了文档中出现了9次，rich是0.36对应文档中出现了3次；右奇异向量中一的第一行表示每一篇文档中的出现词的个数的近似，比如说，T6是0.49，出现了5个词，T2是0.22，出现了2个词。

然后我们反过头来看，我们可以将左奇异向量和右奇异向量都取后2维（之前是3维的矩阵），投影到一个平面上，可以得到：

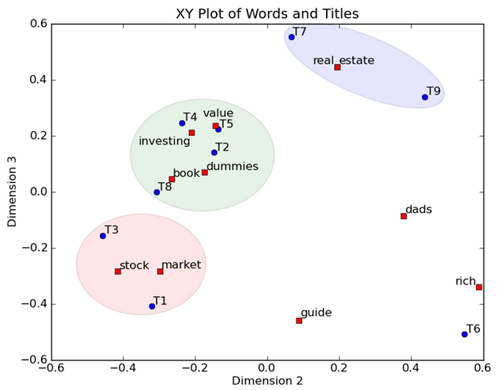
在图上，每一个红色的点，都表示一个词，每一个蓝色的点，都表示一篇文档，这样我们可以对这些词和文档进行聚类，比如说stock 和 market可以放在一类，因为他们老是出现在一起，real和estate可以放在一类，dads，guide这种词就看起来有点孤立了，我们就不对他们进行合并了。

按这样聚类出现的效果，可以提取文档集合中的近义词，这样当用户检索文档的时候，是用语义级别（近义词集合）去检索了，而不是之前的词的级别。这样一减少我们的检索、存储量，因为这样压缩的文档集合和PCA是异曲同工的，二可以提高我们的用户体验，用户输入一个词，我们可以在这个词的近义词的集合中去找，这是传统的索引无法做到的。

对SVD分解与文本挖掘的理解

三、图像压缩

我们来看一个奇异值分解在数据表达上的应用。假设我们有如下的一张 15 x 25 的图像数据。

如图所示，该图像主要由下面三部分构成。

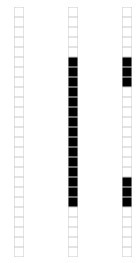
我们将图像表示成 15 x 25 的矩阵，矩阵的元素对应着图像的不同像素，如果像素是白色的话，就取 1，黑色的就取 0. 我们得到了一个具有375个元素的矩阵，如下图所示

如果我们对矩阵M进行奇异值分解以后，得到奇异值分别是

σ 1  = 14.72 
σ 2  = 5.22 
σ 3  = 3.31

矩阵M就可以表示成

M = u 1 σ 1   v 1 T  +  u 2 σ 2   v 2 T  +  u 3 σ 3   v 3 T

v i 具有15个元素， u i  具有25个元素，σ i  对应不同的奇异值。如上图所示，我们就可以用123个元素来表示具有375个元素的图像数据了。

四、去除噪声

前面的例子的奇异值都不为零，或者都还算比较大，下面我们来探索一下拥有零或者非常小的奇异值的情况。通常来讲，大的奇异值对应的部分会包含更多的信息。比如，我们有一张扫描的，带有噪声的图像，如下图所示

我们采用跟实例二相同的处理方式处理该扫描图像。得到图像矩阵的奇异值：

σ 1  = 14.15 
σ 2  = 4.67 
σ 3  = 3.00 
σ 4  = 0.21 
σ 5  = 0.19 
… 
σ 15  = 0.05

很明显，前面三个奇异值远远比后面的奇异值要大，这样矩阵 M 的分解方式就可以如下：

M 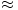     u 1 σ 1   v 1 T  +  u 2 σ 2   v 2 T  +  u 3 σ 3   v 3 T

经过奇异值分解后，我们得到了一张降噪后的图像。

五、数据分析

我们搜集的数据中总是存在噪声：无论采用的设备多精密，方法有多好，总是会存在一些误差的。如果你们还记得上文提到的，大的奇异值对应了矩阵中的主要信息的话，运用SVD进行数据分析，提取其中的主要部分的话，还是相当合理的。

作为例子，假如我们搜集的数据如下所示：

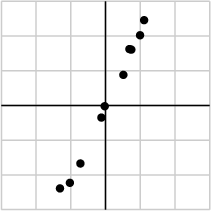
我们将数据用矩阵的形式表示：

经过奇异值分解后，得到

σ 1  = 6.04 
σ 2  = 0.22

由于第一个奇异值远比第二个要大，数据中有包含一些噪声，第二个奇异值在原始矩阵分解相对应的部分可以忽略。经过SVD分解后，保留了主要样本点如图所示

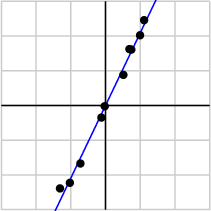
就保留主要样本数据来看，该过程跟PCA( principal component analysis)技术有一些联系，PCA也使用了SVD去检测数据间依赖和冗余信息.

参考资料：

1） http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html 
2）A Tutorial on Principal Component Analysis, Jonathon Shlens 
3） http://www.puffinwarellc.com/index.php/news-and-articles/articles/30-singular-value-decomposition-tutorial.html 
4） http://www.puffinwarellc.com/index.php/news-and-articles/articles/33-latent-semantic-analysis-tutorial.html 
5） http://www.miislita.com/information-retrieval-tutorial/svd-lsi-tutorial-1-understanding.html 
6）Singular Value Decomposition and Principal Component Analysis, Rasmus Elsborg Madsen, Lars Kai Hansen and Ole Winther, 2004 
7） http://blog.sciencenet.cn/blog-696950-699432.html