堆排序
1. 算法思想
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
2. 实现原理
要实现从小到大的排序,就要建立大顶堆,即父节点比子节点都要大。
2.1、初始化数组,创建大顶堆。
1. 大顶堆的创建从下往上比较,不能直接用无序数组从根节点比较,否则有的不符合大顶堆的定义。
2.2、交换根节点和倒数第一个数据,现在倒数第一个数据就是最大的。
2.3、重新建立大顶堆。
1. 因为只有 array[0] 改变,其它都符合大顶堆的定义,所以可以根节点 array[0] 重新建立。
2.4、重复2.2、2.3的步骤,直到只剩根节点 array[0],即 i=1。
3. 动态演示
网上这个就展示的非常好

4. 完整代码
4.1. 核心函数
调整函数:void heap_adjust_max(int* array, int start, int end)
排序函数:void heap_sort(int* array, int size)
4.2. 代码
#include <stdio.h>
#include <stdlib.h> // rand() srand()
#include <time.h> // time()
void display(int* array, int size); // 打印函数
int check_min(int* array, int size); // 检查函数
int check_max(int* array, int size); // 检查函数
void swap(int* a, int* b); // 交换函数
/**
* @brief 从大到小排序:创建小顶堆
*
* @param array 数组首指针
* @param start 调整开始位置
* @param end 调整结束位置
*/
void heap_adjust_min(int* array, int start, int end)
{
int parent = start; // 父节点下标
int child = 2 * start + 1; // 子节点下标
while (child < end) {
// 判断子节点大小,小的与父节点比较
if (child + 1 < end && array[child] > array[child + 1]) {
child++;
}
/**
* 比较父节点和子节点大小
* 小于 表示调整好了,直接退出
* 其他 继续向下调整
*/
if (array[parent] < array[child]) {
return;
} else {
swap(&array[parent], &array[child]); // 交换父节点和子节点
parent = child; // 子节点下标 赋给 父节点下标
child = child * 2 + 1; // 换行,比较下面的父节点和子节点
}
}
}
/**
* @brief 从小到大排序:创建大顶堆
*
* @param array 数组首指针
* @param start 调整开始位置
* @param end 调整结束位置
*/
void heap_adjust_max(int* array, int start, int end)
{
int parent = start; // 父节点下标
int child = 2 * start + 1; // 子节点下标
while (child < end) {
// 判断子节点大小,大的与父节点比较
if (child + 1 < end && array[child] < array[child + 1]) {
child++;
}
/**
* 比较父节点和子节点大小
* 大于 表示调整好了,直接退出
* 其他 继续向下调整
*/
if (array[parent] > array[child]) {
return;
} else {
swap(&array[parent], &array[child]); // 交换父节点和子节点
parent = child; // 子节点下标 赋给 父节点下标
child = child * 2 + 1; // 换行,比较下面的父节点和子节点
}
}
}
/**
* @brief 堆排序
*
* @param array 数组首地址
* @param size 数组大小
*/
void heap_sort(int* array, int size)
{
printf("初始化数组:");
// 初始化堆:倒数一半开始, 因为后面的在最底层不用调整
// 创建大顶堆,必须从下往上比较,否则有的不符合大顶堆定义
for (int i = size / 2 - 1; i >= 0; i--) {
heap_adjust_max(array, i, size);
}
// 查看初始化结果
display(array, size);
// 依次交换排序并调整
for (int i = size - 1; i > 0; i--) {
swap(&array[0], &array[i]); // 交换顶点和第 i 个数据,因为只有 array[0] 改变,其它都符合大顶堆的定义,所以可以从上往下重新建立
heap_adjust_max(array, 0, i); // 需要排序的数组大小逐渐变小,重新建立大顶堆
}
}
int main()
{
// 测试用例
// int array[] = {49, 38, 65, 97, 76, 13, 27, 49, 10};
// int array_size = sizeof(array) / sizeof(array[0]);
// printf("%d n", array_size);
// printf("排序前数组:");
// display(array, array_size);
// heap_sort(array, array_size);
// printf("排序后数组:");
// display(array, array_size);
// 随机测试
int array_num = 20; // 数组数量
int array_size = 20; // 数组大小
int array[array_size]; // 数组初始化
srand((unsigned int)time(NULL)); // 随机数种子,保证每次不一样
for (int i = 0; i < array_num; i++) {
for (int j = 0; j < array_size; j++) {
array[j] = rand() % 1000; // 随机生成数大小 0~999
}
printf("原来的数组:");
display(array, array_size);
heap_sort(array, array_size);
printf("排序后数组:");
display(array, array_size);
// 检测排序结果
if (check_max(array, array_size) != 0) {
exit(-1);
}
printf("n");
}
return 0;
}
/**
* @brief 打印函数
*
* @param array 数组首指针
* @param size 数组大小
*/
void display(int* array, int size)
{
for (int i = 0; i < size; i++) {
printf("%d ", array[i]);
}
printf("n");
}
/**
* @brief 检查函数
*
* @param array 数组首指针
* @param size 数组大小
*/
int check_min(int* array, int size)
{
for (int i = 0; i < size - 1; i++) {
if (array[i] < array[i + 1]) {
printf("sort array fail...n");
return -1;
}
}
printf("sort array success...n");
return 0;
}
int check_max(int* array, int size)
{
for (int i = 0; i < size - 1; i++) {
if (array[i] > array[i + 1]) {
printf("sort array fail...n");
return -1;
}
}
printf("sort array success...n");
return 0;
}
/**
* @brief 交换函数
*
* @param a 第一个交换地址
* @param b 第二个交换地址
*/
void swap(int* a, int* b)
{
int temp = *b;
*b = *a;
*a = temp;
}
5. 结果展示
(显示每次排序结果)
从小到大
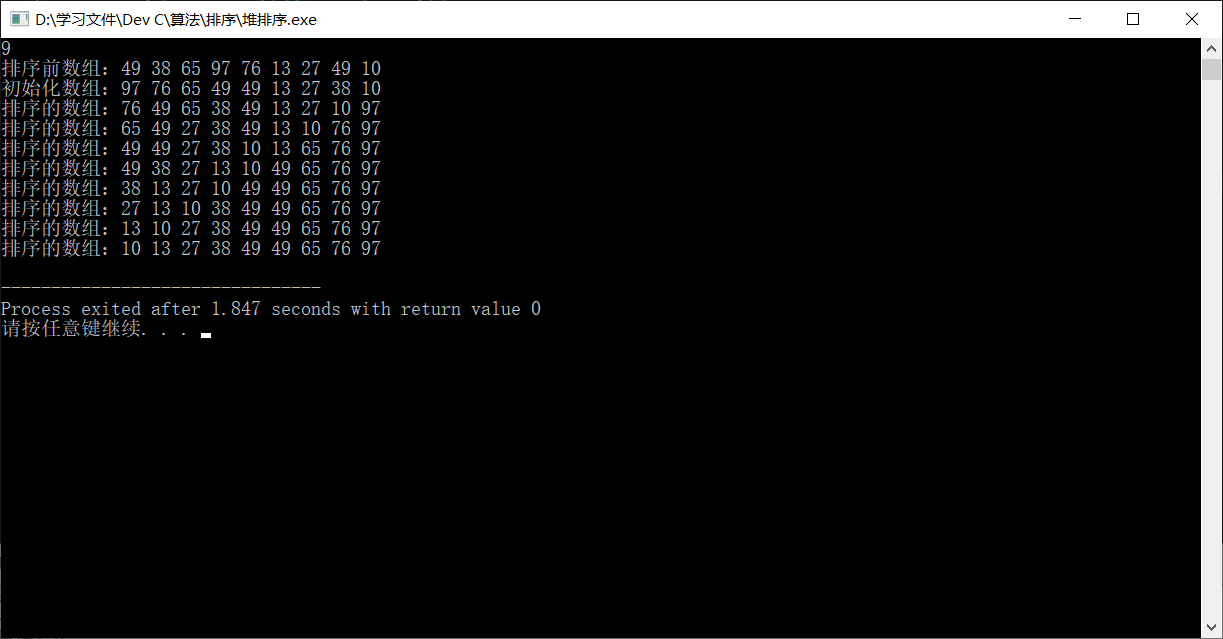 从大到小
从大到小
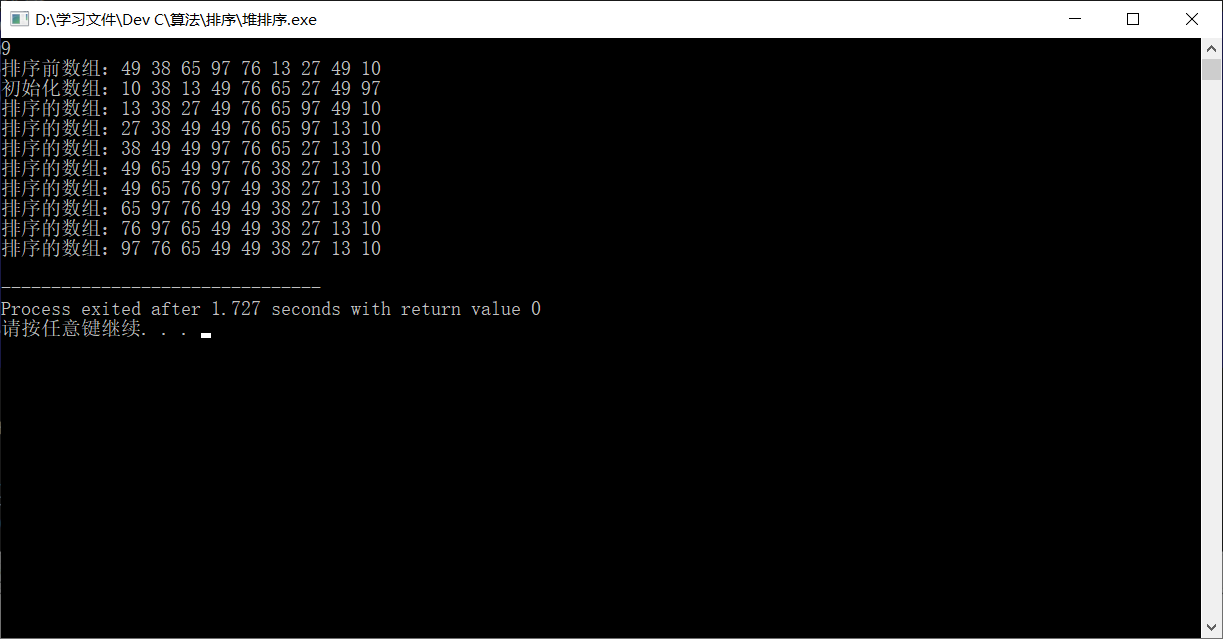
6. 算法分析
时间复杂度:
- 最好:O(n log n)
- 最坏:O(n log n)
- 平均:O(n log n)
空间复杂度:O(1)
稳定性:不稳定
最后
以上就是大方电灯胆最近收集整理的关于堆排序算法——C/C++堆排序的全部内容,更多相关堆排序算法——C/C++堆排序内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。



![[C/C++标准库]_[初级]_[标准库里提供的排序算法]sort()stable_sort()partial_sort()reverse()nth_element()qsort()](https://www.shuijiaxian.com/files_image/reation/bcimg7.png)




发表评论 取消回复