1.问题分析

        给定n种物品和一个背包容量为c的背包，物品i的重量是wi，其价值为vi，利用回溯法来实现求解如何使装入背包中的物品的总价值最大。

2.算法设计思路

（1）物品有n种，背包容量为C，用v[i]和w[i]存储第i种物品的价值和重量，用x[i]标记第i种物品是否装入背包，用bestx[i]存储第i种物品的最优装载方案；

（2）用递归函数Knapsack（i，bv，bw）来实现回溯法搜索子集树（形式参数i表示递归深度，n用来控制递归深度，形式参数bv和bw表示当前总价值和总重量，bestv表示当前最优总价值）；

（3）若i>n，则算法搜索到一个叶子结点，判断当前总价值是否最优；

（4）若bv>bestv，更新当前最优总价值为当前总价值，再更新装载方案；

（5）采用for循环对物品i装与不装两种情况进行讨论（0≤j≤1）：

          1）x[i]=j；

          2）若总重量不大于背包容量（即bw+x[i]*w[i]<=c），则更新当前总价值和总重量（即bw+=w[i]*x[i]，bv+=v[i]*x[i]）, 对物品                     i+1调用递归函数Knapsack (i+1,cp,cw) 继续进行装载；

          3）函数Knapsack (i+1,bv,bw)调用结束后则返回当前总价值和总重量（即 bw-=w[i]*x[i],bv-=v[i]*x[i]）；

          4）当j>1时，for循环结束；

（6）当i=1时，若已测试完所有装载方案，外层调用就全部结束；

（7）主函数调用一次Knapsack (1,0,0)即可完成整个回溯搜索过程，最终得到的bestv和bestx[i]即为所求最大总价值和最优装载方案。

3.算法实现

#include<iostream>
#include<cstdio>
using namespace std;
int n,c,bestv;//物品的个数，背包的容量，最大价值
int v[10000],w[10000],x[10000],bestx[10000];//物品的价值，物品的重量，x[i]暂存物品的选中情况,物品的选中情况

void Knapsack(int i,int bv,int bw)
{
    //bw当前包内物品重量，bv当前包内物品价值
    if(i>n)//回溯结束
    {
        if(bv>bestv)
        {
            bestv=bv;
            for(i=0; i<=n; i++)
                bestx[i]=x[i];
        }
    }
    else
        for(int j=0; j<=1; j++)
        {
            x[i]=j;
            if(bw+x[i]*w[i]<=c)
            {
                bw+=w[i]*x[i];
                bv+=v[i]*x[i];
                Knapsack(i+1,bv,bw);
                bw-=w[i]*x[i];
                bv-=v[i]*x[i];
            }
        }
}

int main()
{
    bestv=0;
    printf("请输入物品个数和背包最大容量:n");
    scanf("%d%d",&n,&c);
    printf("请依次输入物品的价值:n");
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&v[i]);
    }
    printf("请依次输入物品的重量:n");
    for(int i=1; i<=n; i++)
        scanf("%d",&w[i]);
    Knapsack(1,0,0);
    printf("最大价值为:n");
    printf("%dn",bestv);
    printf("被选中的物品依次是(0表示未选中，1表示选中)n");
    for(int i=1; i<=n; i++)
    {
        printf("%d ",bestx[i]);
    }
    printf("n");
    return 0;
}

4.运行结果

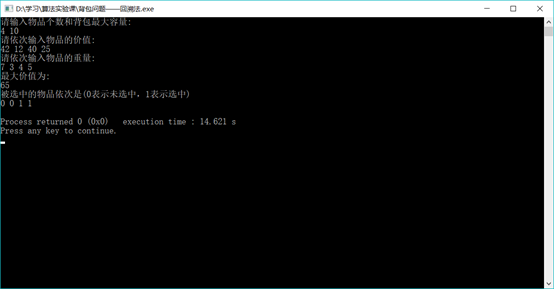
5.算法分析

        计算0-1背包问题的回溯算法的时间复杂度为O(n2的n次方)，在搜索过程中的任何时刻，仅保留从开始结点到当前可扩展结点的路径，其空间需求为O（从开始结点起最长路径的长度）。所以，空间复杂度为O（n）。

6.经验归纳与总结

        对于每个物品若符合约束函数将当前节点加入到活动节点中 ，继续深度探索。若不符合直接将当前节点以及子树"剪枝"处理。当深度探索到叶子节点时。记录下此时背包最优值和对应的物品选择情况。然后从当前叶子节点往上回溯，重复刚才的回溯方法 。注意:  回溯要回溯到根。再由根探索树的另一边子树。当所有节点路径回溯完即可解决问题。

最后

以上就是威武水壶为你收集整理的0/1背包问题（回溯法）1.问题分析2.算法设计思路3.算法实现4.运行结果5.算法分析6.经验归纳与总结 的全部内容，希望文章能够帮你解决0/1背包问题（回溯法）1.问题分析2.算法设计思路3.算法实现4.运行结果5.算法分析6.经验归纳与总结 所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。