Catalan数（卡特兰数）

一.基本公式：

先说明下组合数的公式：

定义：

性质：

递推式：c(n,m)=c(n-1,m-1)+c(n-1,m)

具体证明这里不加赘述，毕竟我们只关心卡特兰数能够解决哪些问题。详细证明请参考维基百科https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%A1%94%E5%85%B0%E6%95%B0

卡特兰数：

求解公式：

递归公式：

1.

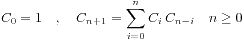
2.h(n)=((4*n-2)/(n+1))*h(n-1);

#include<iostream>
using namespace std;
int n;
unsigned long long c[50];
int get_c1()
{
int i,j,p=1;
for(i=n+1,j=1;i<=2*n;i++,j++)
{
p=p*i/j;
}
return p/(n+1);
}
void get_c2()
{
for(int i=2;i<=30;i++)
{
c[i]=(4*i-2)*c[i-1]/(i+1);
}
}
int main()
{
c[0]=c[1]=1;
get_c2();
while(cin>>n)
{
cout<<"定义： "<<get_c1()<<endl;
cout<<"xingzhi:
"<<c[n]<<endl;
}
}

二.来看几道基本的数学竞赛题：

2003年浙江省小学数学夏令营竞赛考了这个题：圆周上10个点可以连成既不相交，也没有公共端点的5条线段，不同的连法共有_____种。

答：方法的种数是卡特兰数C₅＝42，此题被收录进单墫主编的知识出版社出版的《华数奥赛强化训练》小学六年级册的“计数问题”专题。

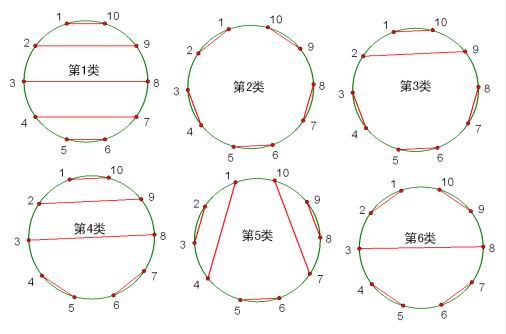
共六种类型，第1类有5种连法，第2类有2种连法，第3类有10种连法，第4类有10种连法，第5类有10种连法，第6类有5种连法。共有42种连法。

1994年《小学数学》有奖征答竞赛：游乐园门票1元一张，每人限购一张。现在有10个小朋友排队购票，其中5个小朋友每人只有1元的钞票一张，另5个小朋友每人只有2元的钞票一张，售票员没有准备零钱。问：有多少种排队方法，使售票员总能找的开零钱？

（此题也被许多奥数资料收录为例题或习题，《华罗庚学校数学课本》小学六年级册的思维训练也收有此题）

答：现把拿1元的5个小朋友看成是相同的，把拿2元的5个小朋友也看成是相同的，使用我们常用的“逐点累加法”：

图中每条小横段表示拿1元的小朋友，每条小竖段表示拿2元的小朋友，要求从A走到B的过程中网格中任何点均有横段数不小于竖段数：拿1元的要先，且人数不能少于拿2元的，即不能越过对角线AB：每个点所标的数即为从A走到此点的方法数。求从A到B的走法的方法数。逐点累加可求出为42，即卡特兰数C₅＝42。

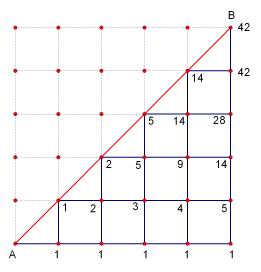
又由于每个小朋友是不相同的，所以共有42×5！×5！＝42×120×120＝604800种情况。

若把此题的10个人，拿1元的有5人，拿2元的有5人改为共有2n个人，拿1元的n人，拿2元的n人，则符合要求的排队方法数为：

再一个卡特兰数的例子：

甲乙两人比赛乒乓球，最后结果为20∶20，问比赛过程中甲始终领先乙的计分情形的种数。

即甲在得到1分到19分的过程中始终领先乙，其种数是卡特兰数

再一个卡特兰数的例子

饭后，姐姐洗碗，妹妹把姐姐洗过的碗一个一个放进碗橱摞成一摞。一共有n个不同的碗，洗前也是摞成一摞的，也许因为小妹贪玩而使碗拿进碗橱不及时，姐姐则把洗过的碗摞在旁边，问：小妹摞起的碗有多少种可能的方式？

答：得数是第n个卡特兰数C_n。

再一个卡特兰数的例子

一个汽车队在狭窄的路面上行驶，不得超车，但可以进入一个死胡同去加油，然后再插队行驶，共有n辆汽车，问共有多少种不同的方式使得车队开出城去？

答：得数是第n个卡特兰数C_n。

三.卡特兰数求解问题汇总

1.括号化问题。

　　矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种)

• Cn= n对括号正确匹配组成的字符串数，例如 3对括号能够组成：

2.出栈次序问题。

　　Cn=一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?

类似：有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)

　　3.三角形问题

• Cn= n+2条边的多边形，能被分割成三角形的方案数，例如 6边型的分割方案有：

　　类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她

　　从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？

　　类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?

• 4.Cn= 拥有 n+1 个叶子节点的二叉树的数量。例如 4个叶子节点的所有二叉树形态：

• 5.Cn= 圆桌周围有 2n个人，他们两两握手，但没有交叉的方案数。

• 6.Cn=n*n的方格地图中，从一个角到另外一个角，不跨越对角线的路径数，例如， 4×4方格地图中的路径有：

最后

以上就是热情鸭子为你收集整理的Catalan数（卡特兰数）的全部内容，希望文章能够帮你解决Catalan数（卡特兰数）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。