简介

莫队是由莫涛队长整理的一种算法，是一种暴力优化的将数据强制离线进行处理的算法。

本文讲介绍几种常见的莫队。但有一个公共前提：莫队算法是个离线算法，对于强制在线的做法是不适用的。与其他很多算法（如树状数组、线段树）类似，莫队算法也用到了分块的思想。

Part 1：普通莫队

原理简述

我们将整一个长度为 $n$ 的数组分成 $\sqrt{n}$ 块。接着，对于任意两个询问 $[l_i,r_i],[l_j,r_j]$，如果 $l_i,l_j$ 所在区间不同，就按区间排序，否则按 $r_i,r_j$ 排序。

排完序后，我们从 $1$ 到 $\sqrt{n}$ 处理每一个块的查询，最终就可以得到结果。

下面是一波不算强的强势图解：

设数组长度为 $9$，有以下询问：$(1,9),(7,8),(2,4),(1,7),(4,9),(5,6),(5,8),(3,6)$。

1. 排序，排序完后如图所示：
   
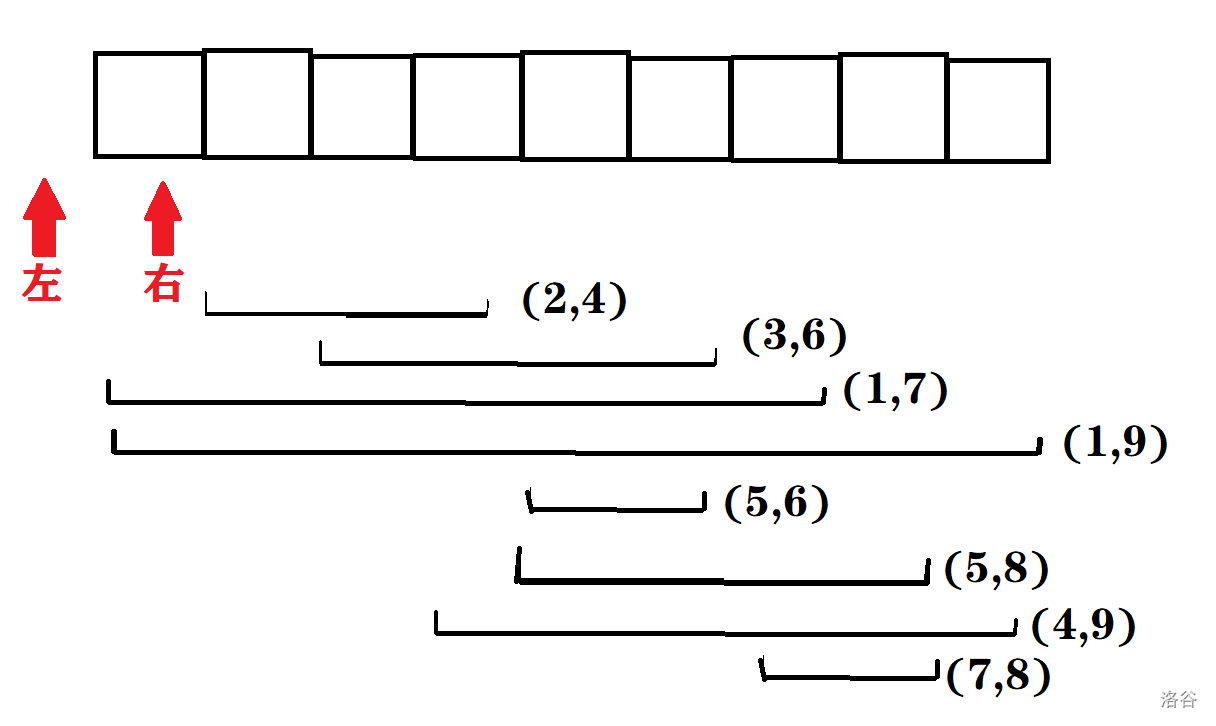
2. 操作。

• 定义一个左指针 $s$ 和一个右指针 $t$，初始时是一个空区间，即$s=1,t=0$（注意 $t=1$ 不是空区间，还有一个元素）。
• 第一组询问：$l=2,r=4$。将左右指针移动到对应位置后，如图：
  
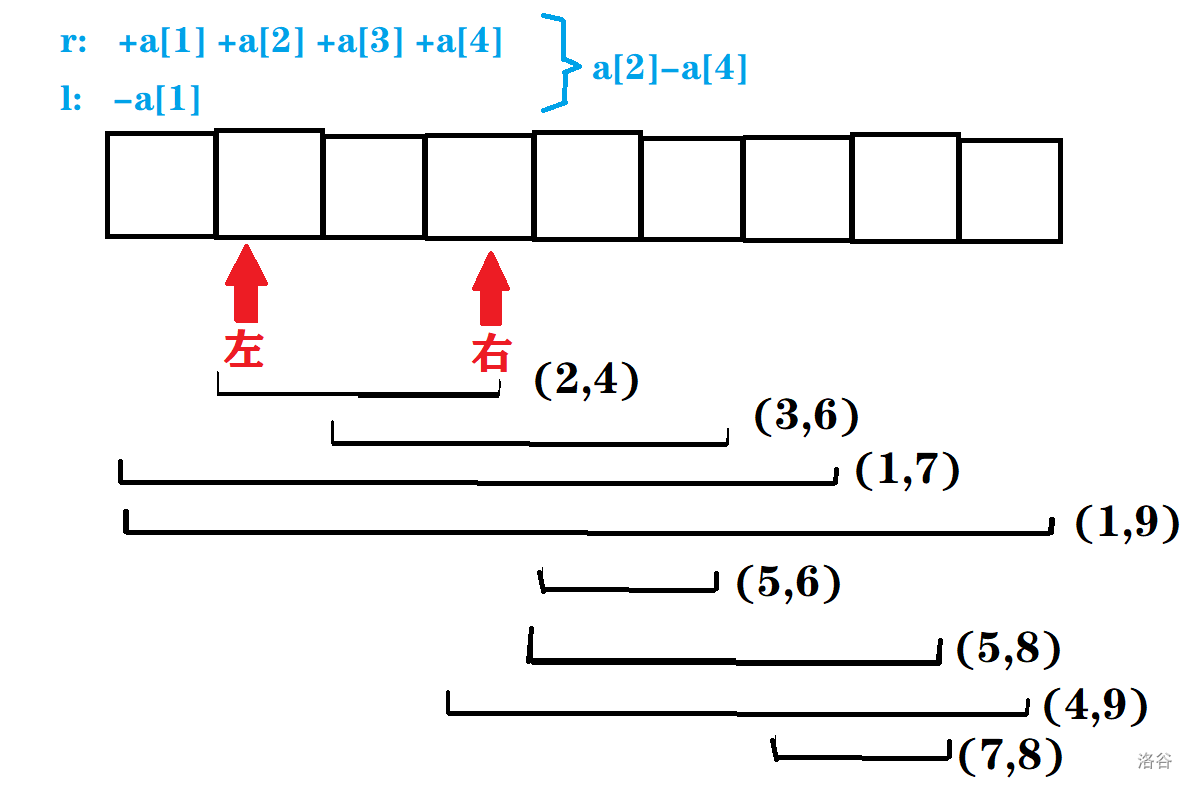
• 第二组询问：$l=3,r=6$。将左右指针移动到对应位置后，如图：
  
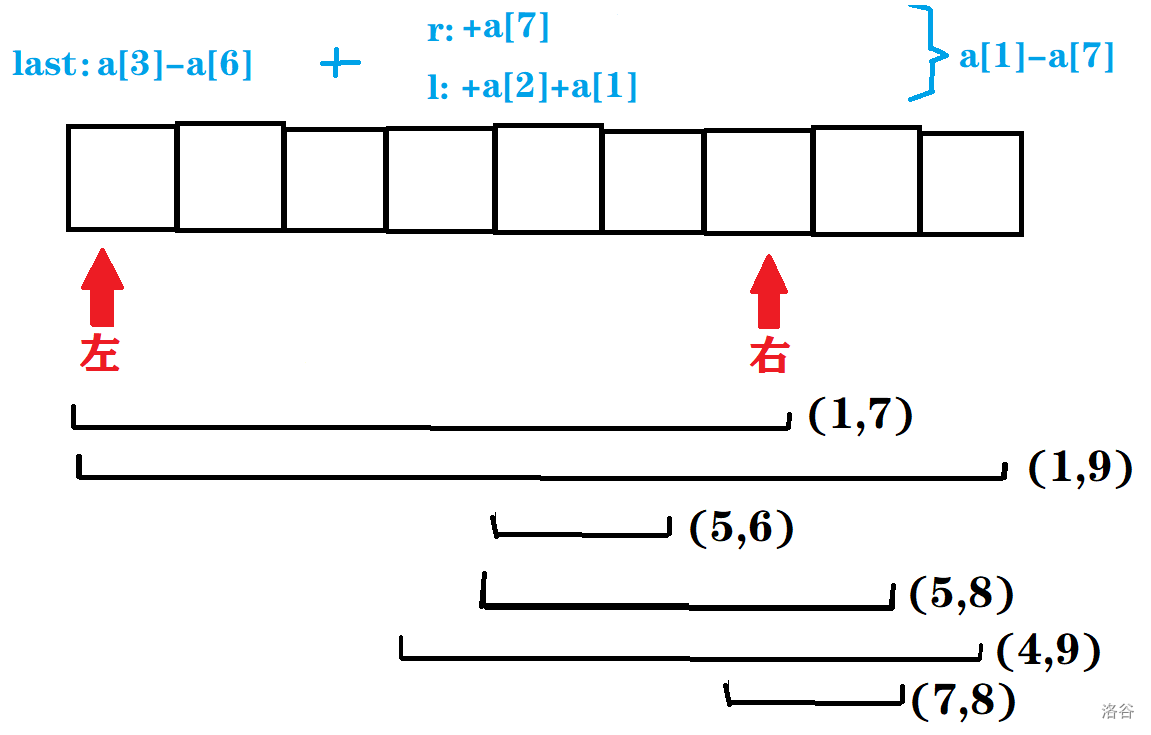
• 第二组询问：$l=3,r=6$。将左右指针移动到对应位置后，如图：
  
• 以此类推，剩下的询问都是这么操作，直到得出最后结果。

看完图示，相信大家应该对莫队的原理有一定的了解了。

复杂度分析

开门见山：莫队算法的时间复杂度是 $O(n\sqrt{n})$。

罕见地证明一下：
首先易得莫队的复杂度主要体现在左右指针的移动上。那我们分左右指针探讨复杂度。

• 左指针 $s$：

1. 因为有 $\sqrt{n}$ 块，所以 $s$ 在区间间跳动的复杂度是 $O(\sqrt{n})$，总距离 $O(n)$。
2. 由 1 可得在同一个块内转移次数为 $O(n-\sqrt{n})$，加上每次查询的时间复杂度是 $O(\sqrt{n})$，可得 $s$ 的总复杂度为 $O(n)+O(n-\sqrt{n})\times O(\sqrt{n})=O(n\sqrt{n})$。

• 右指针 $t$：

1. $t$ 在每一个 $s$ 的转移时间为 $O(n)$（因为排序没有要求右指针的排列，所以它是无序的）。
2. 又因为一共有 $\sqrt{n}$ 块，所以 $t$ 的时间复杂度为 $O(n\sqrt{n})$。

综上所述，莫队算法的时间复杂度就是 $O(n\sqrt{n})$。

例题

P1494 小z的袜子。

首先想到暴力：每次枚举 $[l,r]$ 暴力求解。时间复杂度 $O(nm)$，妥妥的 Time Limit Enough 。

因为是静态区间询问，并且没有强制在线，所以考虑莫队。

设 $cn{t}_i$ 为当前区间第 $i$ 种颜色数量。对于一个区间 $[l,r]$，一共有 $C_{r-l+1}^2$ 种选法；每一对袜子对这个区间的的贡献为 $C_{cn{t}_i}^2$，最后求个最大公因数约分，问题就解决了。

Code：

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N = 50000 + 10;
int n, m, now, k, cnt[N], ret[N], a[N];
struct query{int l, r, id;} q[N];

bool cmp(query i, query j){
	if(i.l / k != j.l / k)	return i.l < j.l;//注意不是 i.l < j.l
	return i.r < j.r;
}

bool cmp2(query i, query j){return i.id < j.id;}//输出答案用的

void add(int x){
	now -= cnt[x] * (cnt[x] - 1) / 2;//减去不在区间内的元素
	cnt[x]++;
	now += cnt[x] * (cnt[x] - 1) / 2;//加上新的元素
}

void del(int x){
	now -= cnt[x] * (cnt[x] - 1) / 2;//减去不在区间内的元素
	cnt[x]--;
	now += cnt[x] * (cnt[x] - 1) / 2;//加上新的元素
}

signed main(){
	scanf("%lld%lld", &n, &m);
	for(int i=1;i<=n;i++)	scanf("%lld", &a[i]);
	for(int i=1;i<=m;i++){
		scanf("%lld%lld", &q[i].l, &q[i].r);
		q[i].id = i;
	}
	k = sqrt(n);//排序要用
	sort(q + 1, q + 1 + m, cmp);
	int s = 1, t = 0;//表示空区间
	//注意:s=1, t=1不是空区间，还有一个元素 
	for(int i=1;i<=m;i++){//以下四步结合图解理解
		while(s > q[i].l)	add(a[--s]);
		while(t < q[i].r)	add(a[++t]);
		while(s < q[i].l)	del(a[s++]);
		while(t > q[i].r)	del(a[t--]);
		ret[q[i].id] = now;//记录答案
	}
	sort(q + 1, q + 1 + m, cmp2);
	for(int i=1;i<=m;i++){
		if(q[i].r == q[i].l){
			printf("0/1n");
			continue;
		}//题目数据特判
		int tot = (q[i].r - q[i].l + 1) * (q[i].r - q[i].l) / 2;//总共选法
		int g = __gcd(ret[i], tot);//约分用的
		printf("%lld/%lldn", ret[i] / g, tot / g);
	}
	return 0;
}

Part 2：带修莫队

原理

其实这东西是跟普通莫队一起学的，但可能题练得少，再看的时候已经没印象了。

带修莫队其实就是在普通莫队上加了个时间维度。类似主席树，我们在每次的查询操作中，记录一个 $ver$ 表示当前查询是基于第几个版本的。当然，这里的查询不算一个新版本，只有更新的时候才会产生新版本。

两个查询的 $ver$ 越相近，证明它们版本的相似度越高，更新次数就越少。但因为其不涉及到左右指针的移动，并且相对来说操作次数较小，所以我们将其作为第三关键字排序，仍然以左右端点作为主要对象。

时间复杂度分析

这个东西显然跟莫队的块长有关系，直接上结论：每块大小在 $n^{\frac{2}{3}}$ 时会有最优复杂度。

怎么取到这个数的我就不讲了，因为证明过程十分复杂，解出来一堆带未知数的东西。我来分析分析移动指针的复杂度（假设 $n,m$ 同阶）：

• 左指针：每个询问最多移动 $n^{\frac{2}{3}}$ 次（全为块内移动），$n$ 次询问总共 $O(n^{\frac{5}{3}})$。
• 右指针：每次询问最多 $n$ 次，但左端点在一个块内时，右指针单调上升，即它最多只会“重置” $n^{\frac{2}{3}}$ 次（每块重置一次），总时间复杂度 $O(n^{\frac{5}{3}})$。
• 时间指针：左右端点皆一致时，$t$ 指针单调上升。而左右端点最多只会变动 $n^{\frac{1}{3}}\times n^{\frac{1}{3}}=n^{\frac{2}{3}}$，加上同块内转移的 $O(n)$，时间复杂度 $O(n^{\frac{5}{3}})$。

综上，三个指针移动的总次数都是 $O(n^{\frac{5}{3}})$，所以总时间复杂度就是 $O(n^{\frac{5}{3}})$。

剩下的就跟普通莫队是一样的了，就是开多一个 $c$ 表示当前版本号，在 $s,t$ 指针移动完之后加个版本号的判断即可。

例题

P1903 是一道不错的题，但是网上到处都是，所以这里给 P2464 的题解，而 P1903 就作为练习题使用。

Part 3：树上莫队

树上莫队其实挺简单的。

显然不可能直接在树上放两个指针瞎搞，你都不知道往哪跳。

想想我们的树链剖分是怎么做的：化树成链，再用数据结构维护区间信息。树上莫队同样运用到了化树成链的思想。

化树成链其实有两种方法，取决于题目问什么。

$dfn$ 序

这个 $dfn$ 序跟树剖是一样的，就是记录这个节点是第几个被访问到的。所以，一个子树的 $dfn$ 序是连续的（它们总是同时被遍历），因此碰到与子树相关的问题时，树上莫队的杀伤力是非常强的。

但是这种方式能被下面的东西代替，所以我们基本上用不到。

Euler 序（dfs 序）

一字之差的确大有不同。我们介绍一下。

原理

dfs 序的原理跟 dfn 序是一样的，但是它的不同之处在于，每个节点进去记一次，出来记一次。

什么意思呢？看图吧。

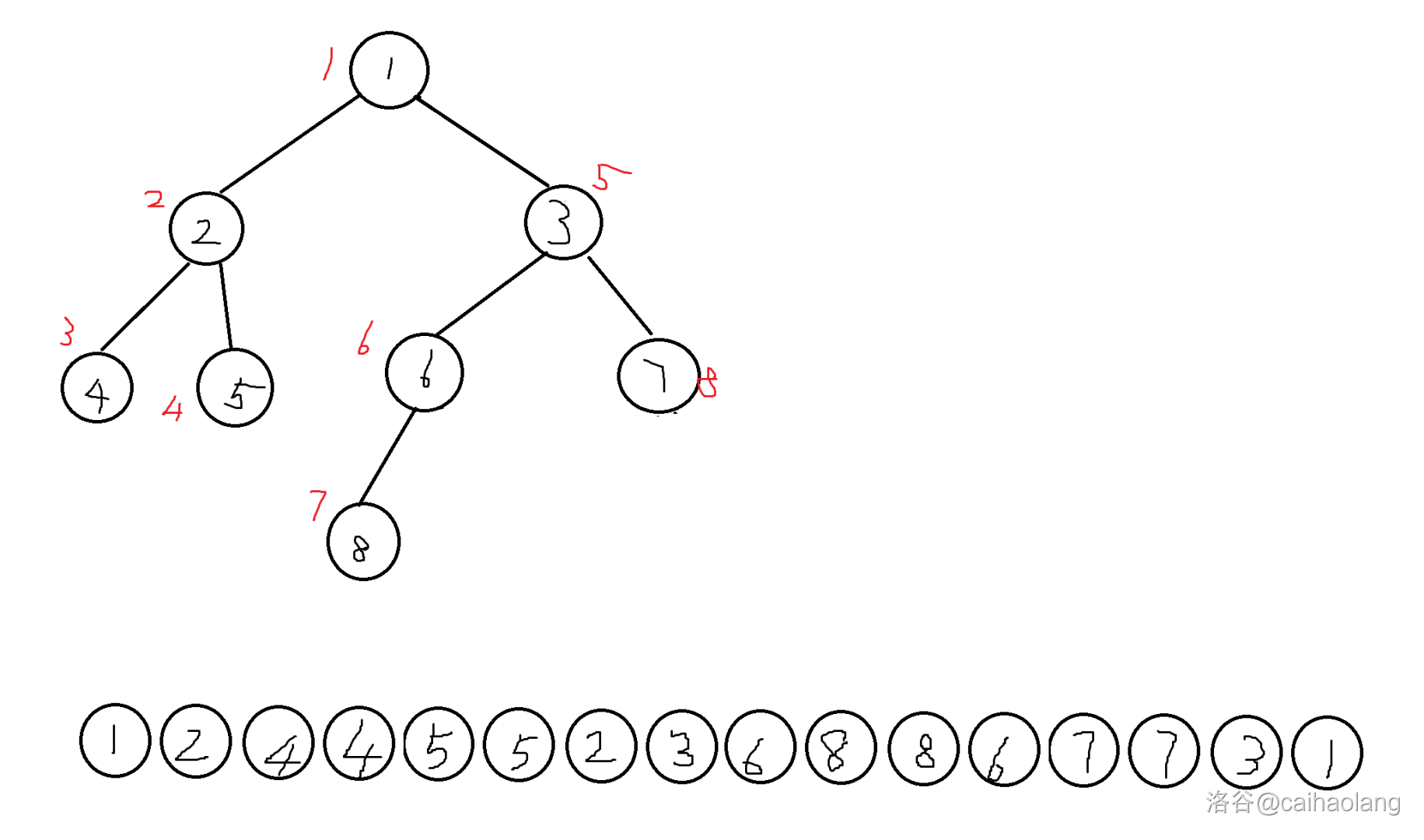如图，这是一棵树。红色笔是它们的 dfn 序，下面是整棵树的 dfs 序。

你会发现每个点都出现两次。是的，dfs 序按照 dfs 的顺序往下遍历，当进入以 $u$ 为根的子树时，就放一个 $u$ 进 dfs 序；离开以 $u$ 为根的子树时，再放一个 $u$ 进去。

这样，第一个 $u$ 就是“进来”的地方，第二个 $u$ 就是“出去”的地方，我们分别记为 $i{n}_u$ 和 $ou{t}_u$。

来看些性质吧：

1. 祖先关系路径：如果两个点 $u,v$，有其中一个是它们的 LCA，那么 $u,v$ 两点的路径就是 $i{n}_u$ 和 $i{n}_v$ 之间只出现过一次的点。比如 $1,8$ 两个点，它们的 $in$ 之间就是 $1244552368$，出现一次的就是 $1368$，正好是 $1$ 到 $8$ 的路径。
2. 非祖先关系路径：如果两个点 $u,v$，有其中一个是它们的 LCA，那么 $u,v$ 两点的路径就是 $ou{t}_u$ 和 $i{n}_v$ 或者 $ou{t}_v$ 和 $i{n}_u$ 之间（哪两个挨得近就是哪个）只出现过一次的点，加上 LCA 这个点。比如 $7,8$ 两个点，它们之间就是 $867$，加个 LCA，就是 $3$，$8673$ 正好是它们的路径。

也就是说，两点之间的路径问题，我们可以转化为区间了！

同时，$u$ 的子树就是 $i{n}_u$ 和 $ou{t}_u$ 之间的所有点了，所以子树问题也可以解决。

这跟莫队联系非常大。因为出现两次的点不在路径上，所以当这个点第一次出现时，我们就添加信息；第二次出现时，我们就删除信息。

例题

然后就做完了。我们来看看例题吧：SP10707 Count on a tree II。

这个题就是把数颜色搬到树上，按上述步骤把其化为序列问题就可以用莫队解决。

注意倍增 LCA dfs 的时候传参是 dfs(1, 1) 而不是 dfs(1, 0)。

struct event{
	int s, t, idx;
	bool operator < (const event &p) const {
		if(s / blk != p.s / blk)
			return s < p.s;
    	return t < p.t;
	}
} q[M];

void add(int u, int v){
	to[++id] = v;
	nxt[id] = head[u], head[u] = id;
}

void dfs(int u, int fa){
	f[u][0] = fa;
	in[u] = ++clk, euler[clk] = u;
	for(int i=1;i<=16;i++)
		f[u][i] = f[f[u][i - 1]][i - 1];
	for(int i=head[u];i;i=nxt[i]){
		int v = to[i];
		if(v == fa)
			continue;
		dep[v] = dep[u] + 1;
		dfs(v, u);
	}
	out[u] = ++clk, euler[clk] = u;
}

int lca(int u, int v){
	if(dep[u] < dep[v])
		swap(u, v);
	for(int i=16;i>=0;i--)
		if(dep[f[u][i]] >= dep[v])
			u = f[u][i];
	if(u == v)
		return u;
	for(int i=16;i>=0;i--)
		if(f[u][i] != f[v][i])
			u = f[u][i], v = f[v][i];
	return f[u][0];
}

void calc(int k){
	if(vis[k])
		tot -= (--tcol[col[k]] == 0);
	else
		tot += (++tcol[col[k]] == 1);
	vis[k] ^= 1;//每出现一次，这个点是否被统计的状态一定会发生改变 
	//统计出现次数也能做 
}

int main(){
	scanf("%d%d", &n, &m);
	for(int i=1;i<=n;i++)
		scanf("%d", &col[i]), a[i] = col[i];
	sort(a + 1, a + 1 + n);
	int len = unique(a + 1, a + 1 + n) - a - 1;
	for(int i=1;i<=n;i++)
		col[i] = lower_bound(a + 1, a + 1 + len, col[i]) - a;
	for(int i=1,u,v;i<n;i++){
		scanf("%d%d", &u, &v);
		add(u, v), add(v, u);
	}
	dfs(1, 1);
	blk = sqrt(clk);
	for(int i=1,u,v;i<=m;i++){
		scanf("%d%d", &u, &v);
		if(in[u] > in[v])
			swap(u, v);//保证 in[u] < in[v]，这样 LCA(u,v) 一定不会等于 v 
		if(lca(u, v) == u)
			q[i] = (event){in[u], in[v], i};
		else
			q[i] = (event){out[u], in[v], i};
		//有个细节：u比v先进，如果u比v后出，那就是上面那种情况，所以必定 out[u]<out[v]
		//而欧拉序遍历的是子树，只有包含关系而没有交错关系，所以 out[u] 必定小于 in[v]
	}
	sort(q + 1, q + 1 + m);
	int l = 1, r = 0;
	for(int i=1;i<=m;i++){
		while(r < q[i].t)
			calc(euler[++r]);
		while(l > q[i].s)
			calc(euler[--l]);
		while(r > q[i].t)
			calc(euler[r--]);
		while(l < q[i].s)
			calc(euler[l++]);
		int chl = lca(euler[q[i].s], euler[q[i].t]);
		if(chl != euler[q[i].s] && chl != euler[q[i].t])
			calc(chl);//记得计算 LCA 的贡献 
		ans[q[i].idx] = tot;
		if(chl != euler[q[i].s] && chl != euler[q[i].t])
			calc(chl);//别忘了还原
	}
	for(int i=1;i<=m;i++)
		printf("%dn", ans[i]);
	return 0;
}

Part 4：回滚莫队

Part 5：莫队二次离线

至此，莫队的几种常用的类型都已讲述完毕。但因为其同样大量运用到了分块的思想，所以十分适合与各种各样奇奇怪怪的分块配合（Ynoi 警告），形成巨大的杀伤力，用途十分广泛，是需要掌握的重要算法之一。

最后

以上就是轻松楼房为你收集整理的莫队全家桶 学习笔记简介Part 1：普通莫队Part 2：带修莫队Part 3：树上莫队Part 4：回滚莫队Part 5：莫队二次离线的全部内容，希望文章能够帮你解决莫队全家桶 学习笔记简介Part 1：普通莫队Part 2：带修莫队Part 3：树上莫队Part 4：回滚莫队Part 5：莫队二次离线所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。