栈简介(先入后出)
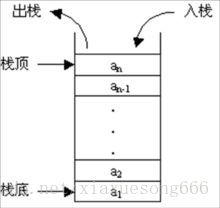
栈(stack)又名堆栈,它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
队列简介(先入先出)
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
顺序队列:
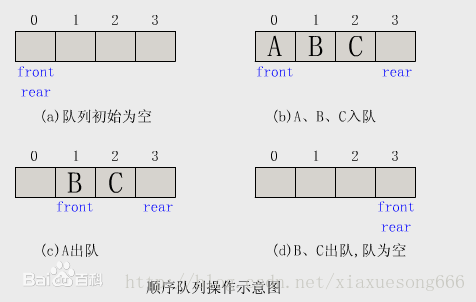
建立顺序队列结构必须为其静态分配或动态申请一片连续的存储空间,并设置两个指针进行管理。一个是队头指针front,它指向队头元素;另一个是队尾指针rear,它指向下一个入队元素的存储位置。
每次在队尾插入一个元素是,rear增1;每次在队头删除一个元素时,front增1。随着插入和删除操作的进行,队列元素的个数不断变化,队列所占的存储空间也在为队列结构所分配的连续空间中移动。当front=rear时,队列中没有任何元素,称为空队列。当rear增加到指向分配的连续空间之外时,队列无法再插入新元素,但这时往往还有大量可用空间未被占用,这些空间是已经出队的队列元素曾经占用过得存储单元。
顺序队列中的溢出现象:
(1) “下溢”现象:当队列为空时,做出队运算产生的溢出现象。“下溢”是正常现象,常用作程序控制转移的条件。
(2)”真上溢”现象:当队列满时,做进栈运算产生空间溢出的现象。“真上溢”是一种出错状态,应设法避免。
(3)”假上溢”现象:由于入队和出队操作中,头尾指针只增加不减小,致使被删元素的空间永远无法重新利用。当队列中实际的元素个数远远小于向量空间的规模时,也可能由于尾指针已超越向量空间的上界而不能做入队操作。该现象称为”假上溢”现象。
循环队列
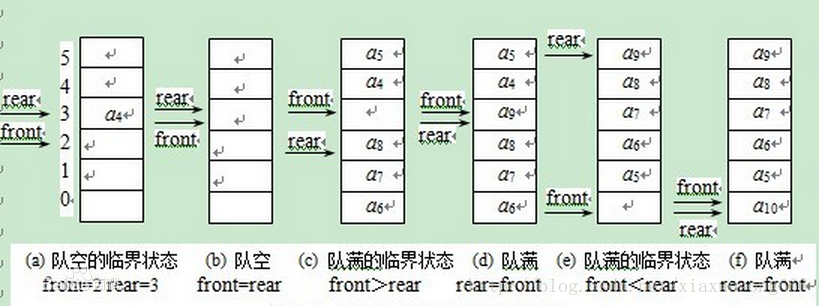
在实际使用队列时,为了使队列空间能重复使用,往往对队列的使用方法稍加改进:无论插入或删除,一旦rear指针增1或front指针增1 时超出了所分配的队列空间,就让它指向这片连续空间的起始位置。自己真从MaxSize-1增1变到0,可用取余运算rear%MaxSize和front%MaxSize来实现。这实际上是把队列空间想象成一个环形空间,环形空间中的存储单元循环使用,用这种方法管理的队列也就称为循环队列。除了一些简单应用之外,真正实用的队列是循环队列。[2]
在循环队列中,当队列为空时,有front=rear,而当所有队列空间全占满时,也有front=rear。为了区别这两种情况,规定循环队列最多只能有MaxSize-1个队列元素,当循环队列中只剩下一个空存储单元时,队列就已经满了。因此,队列判空的条件时front=rear,而队列判满的条件时front=(rear+1)%MaxSize。
1.题目:实现一个特殊的栈,在实现栈的基本功能的基础上,再实现返回栈中最小元素的操作。
1、 pop、push、getMin操作的时间复杂度都是O(1)。
2.、设计的栈类型可以使用现成的栈结构。
【思路】首先定义两个列表来存储,输入的数字和当前栈中最小的数字,接下来定义三种方法,注意的是在push时需要注意比较当前进栈的数字和当前最小的栈内元素进行比较,若当前进栈的数字更小,需要将新数字压入stackMin中(之所以那么做,是为了发生出栈后,无需在栈内寻找最小元素)
class NewStack1:
def __init__(self):
self.stackData = []
self.stackMin = []
def push(self, newNum):
self.stackData.append(newNum)
if len(self.stackMin) == 0 or newNum <= self.getMin():
self.stackMin.append(newNum)
def pop(self):
if len(self.stackData) == 0:
raise Exception("stack is empty!")
value = self.stackData.pop()
if self.getMin() == value:
self.stackMin.pop()
return value
def getMin(self):
if len(self.stackMin) == 0:
raise Exception("stack is empty!")
return self.stackMin[-1]
stack1=NewStack1()
stack1.push(3)
stack1.push(1)
stack1.push(2)
print(stack1.pop())
print(stack1.getMin())2.题目 :编写一个类,用两个栈实现队列,支持队列的基本操作(add, poll, peek)。
【思路】使用两个栈stack1、stack2,stack1栈负责压入数据、stack2栈负责将stack1中的元素逆序,用于获取或者弹出栈顶元素。但是有一个规则:stack2只有为空的时候才再次向stack1栈索要元素,而且,必须一次拿走stack1中当前的所有元素。
| 名称 | 作用 | 说明 |
|---|---|---|
| add | 增加一个元素 | 如果队列已满,则抛出一个IIIegaISlabEepeplian异常 |
| remove | 移除并返回队列头部的元素 | 如果队列为空,则抛出一个NoSuchElementException异常 |
| element | 返回队列头部的元素 | 如果队列为空,则抛出一个NoSuchElementException异常 |
| offer | 添加一个元素并返回true | 如果队列已满,则返回false |
| poll | 移除并返问队列头部的元素 | 如果队列为空,则返回null |
| peek | 返回队列头部的元素 | 如果队列为空,则返回null |
| put | 添加一个元素 | 如果队列满,则阻塞 |
| take | 移除并返回队列头部的元素 | 如果队列为空,则阻塞 |
class stack2Queue:
def __init__(self):
self.stack1=[]
self.stack2=[]
def add(self,newNum):
self.stack1.append(newNum)
def poll(self):
#from ‘not self.stack’ judge whether the stack is empty ,another method if stack ==[]
if not self.stack1 and not self.stack2:
raise Exception('Queue is empty!')
elif not self.stack2:
while(self.stack1):
self.stack2.append(self.stack1.pop())
return self.stack2.pop()
def peek(self):
#from ‘not self.stack’ judge whether the stack is empty ,another method if stack ==[]
if not self.stack1 and not self.stack2:
raise Exception('Queue is empty!')
elif not self.stack2:
while(self.stack1):
self.stack2.append(self.stack1.pop())
return self.stack2[-1]
Queue1=stack2Queue()
Queue1.add(1)
Queue1.add(2)
Queue1.add(3)
print(Queue1.peek())
print(Queue1.poll())
print(Queue1.peek())3.仅用递归函数和栈操作逆序一个栈
一个栈依次压入1、2、3、4、5,那么从栈顶到栈底分别为5、4、3、2、1。将这个栈转置后,从栈顶到栈底为1、2、3、4、5,也就是实现栈中元素的逆序,但是只能用递归函数实现,不能使用其他数据结构。
【思路】
1.不按题目说用递归函数的话,当然只用调用reverse()即可,略过不提。
2.递归方法分为两个部分:
①是将栈底的元素返回并移除
②是逆序这个栈
class StackReverse:
#一直的递归一直到栈底,并一直将栈底元素放到last向上传递,最后剩下去除栈底元素的栈,返回栈底元素
def getandRemove(self,A):
res = A.pop()
if len(A)==0:
return res
else:
last = self.getandRemove(A)
A.append(res)
return last
#将栈底元素再次压入栈中,一直到将整个栈的元素逆序
def reverseStack(self, A,n):
if len(A) == 0:
return
i = self.getandRemove(A)
self.reverseStack(A,len(A))
A.append(i)
return A4.用一个栈实现另一个栈的排序
一个栈中元素的类型是整型,现在想将该栈从顶到底按从大到小的顺序排序,只许申请一个栈。除此之外,可以申请新的变量,但不能申请额外的数据结构。
【思路】 这道题和汉诺塔的思想基本是一样 的,不断将栈顶元素cur弹出,如果新栈为空、或者新栈栈顶元素大于cur,直接将cur压入新栈中;否则,将新栈中所有的元素压回原来的栈中,再将cur压入新栈中.继续弹出原来栈的栈顶元素,重复上述操作即可。
def sortByStack(stack):
#若stack只有一个元素,直接返回
if len(stack) < 2:
return stack
stack1 = []
while stack:
cur = stack.pop()
#新栈为空或者是新栈栈顶元素大于cur
if len(stack1) == 0 or stack1[-1] >= cur:
stack1.append(cur)
else:
while stack1:
#将新栈中的元素全部存入到待排序的stack中
stack.append(stack1.pop())
stack1.append(cur)
#最终将stack1中的元素存入到stack中
while stack1:
stack.append(stack1.pop())
return stack5.生成窗口最大值数组
有一个整型数组arr和一个大小为w的窗口从数组的最左边滑到最右边,窗口每次向右滑动一个位置。
例如,数组为[4,3,5,4,3,3,6,7],窗口大小为3时:依次出现的窗口为[4,3,5], [3,5,4], [5,4,3], [4,3,3], [3,3,6], [3,6,7]。
如果数组长度是n,窗口大小是w,则一共产生n-w+1个窗口。
请实现一个函数。
1、输入:整型数组arr,窗口大小w
2、输出:一个长度大小为n-w+1的数组res,res[i]表示每一种窗口下的最大值。例如上面的例子,应该返回[5,5,5,4,6,7]。
【基本思路】使用双端队列,遍历一遍数组,假设遍历到的位置是 i,如果队列为空或者队尾所对应的元素大于arr[i],将位置 i 压入队列;否则将队尾元素弹出,再将 i 压入队列。此时,判断队头元素是否等于i - w,如果是的话说明此时队头已经不在当前窗口的范围内,删去。这样,这个队列就成了一个维护窗口为w的子数组的最大值更新的结构,队头元素就是每个窗口的最大值。
def getMaxWindow(arr, w):
if arr == None or w < 1 or len(arr) < w:
return
deque = []
res = []
for i in range(len(arr)):
while deque and arr[deque[-1]] <= arr[i]:
deque.pop()
deque.append(i)
if deque[0] <= i - w:
deque.pop(0)
if i-w+1 >= 0:
res.append(arr[deque[0]])
return res方法二:将窗口元素放到某一个列表中并得到其中的最大值,将最大值存储到一个新的list中
def getList(list1,w):
list3=[]
#如果窗口值为1,那么直接返回
if w =1:
return list1
#窗口值小于1报错
elif w<0:
raise Exception ('the length of w is small than 1')
elif len(list1)>=w:
list2=[]
list3=[]
#将前w个元素放入list2中
for i in range(w):
list2.append(list1[i])
#将当前的最大值添加到list3中,这里可以直接使用一个list完成,拿出w为存储窗口值,其他的位存储窗口的最大值,返回时只返回这些最大值即可
list3.append(getMax(list2))
for j in range(w,len(list1)):
print (j)
list2.append(list1[j])
list2=list2[1:]
list3.append(getMax(list2))
return list3
#得到当前列表的最大值
def getMax(list4):
t=0
for k in range(len(list4)):
if list4[k] > t:
t=list4[k]
return t
list0=[4,3,5,4,3,3,6,7]
w=3
print(getList(list0,w)) 6.构造数组的MaxTree
定义二叉树节点如下:
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None 一个数组的MaxTree定义如下:
1、数组中必须没有重复元素
2、MaxTree是一棵二叉树,数组的每一个值对应一个二叉树的节点
3、包括MaxTree树在内且在其中的每一棵子树上,值最大的节点就是树的头。
给定一个没有重复元素的数组arr,写出生成这个数组的MaxTree的函数,要求如果数组长度为N,则时间复杂度为O(N)、额外空间复杂度为O(N)
参考资料:
1.题目来源于《程序员代码面试指南—IT名企算法与数据结构题目最优解》
2.https://github.com/Liwenbin1996/Data_Structures_and_Algorithms
3.http://blog.csdn.net/qq_34342154/article/details/77918297
最后
以上就是直率枕头最近收集整理的关于python数据结构1 栈和队列问题的全部内容,更多相关python数据结构1内容请搜索靠谱客的其他文章。








发表评论 取消回复