LeetCode133-克隆图（附详细测试用例构建方法）

54 阅读 0 评论 36 点赞

我是靠谱客的博主时尚发夹，最近开发中收集的这篇文章主要介绍LeetCode133-克隆图（附详细测试用例构建方法），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

今天最最最开心激动的一件事

就是自己的论文终于出版了

虽然是一篇口碑不好的文章

但还是有些激动啊

千里之行始于足下

希望自己有个好的前景

题目描述：

给你无向连通图中一个节点的引用，请你返回该图的深拷贝（克隆）。

图中的每个节点都包含它的值 val（int）和其邻居的列表（list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1，第二个节点值为 2，以此类推。该图在测试用例中使用邻接列表表示。

邻接列表是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将给定节点的拷贝作为对克隆图的引用返回。

示例 1：

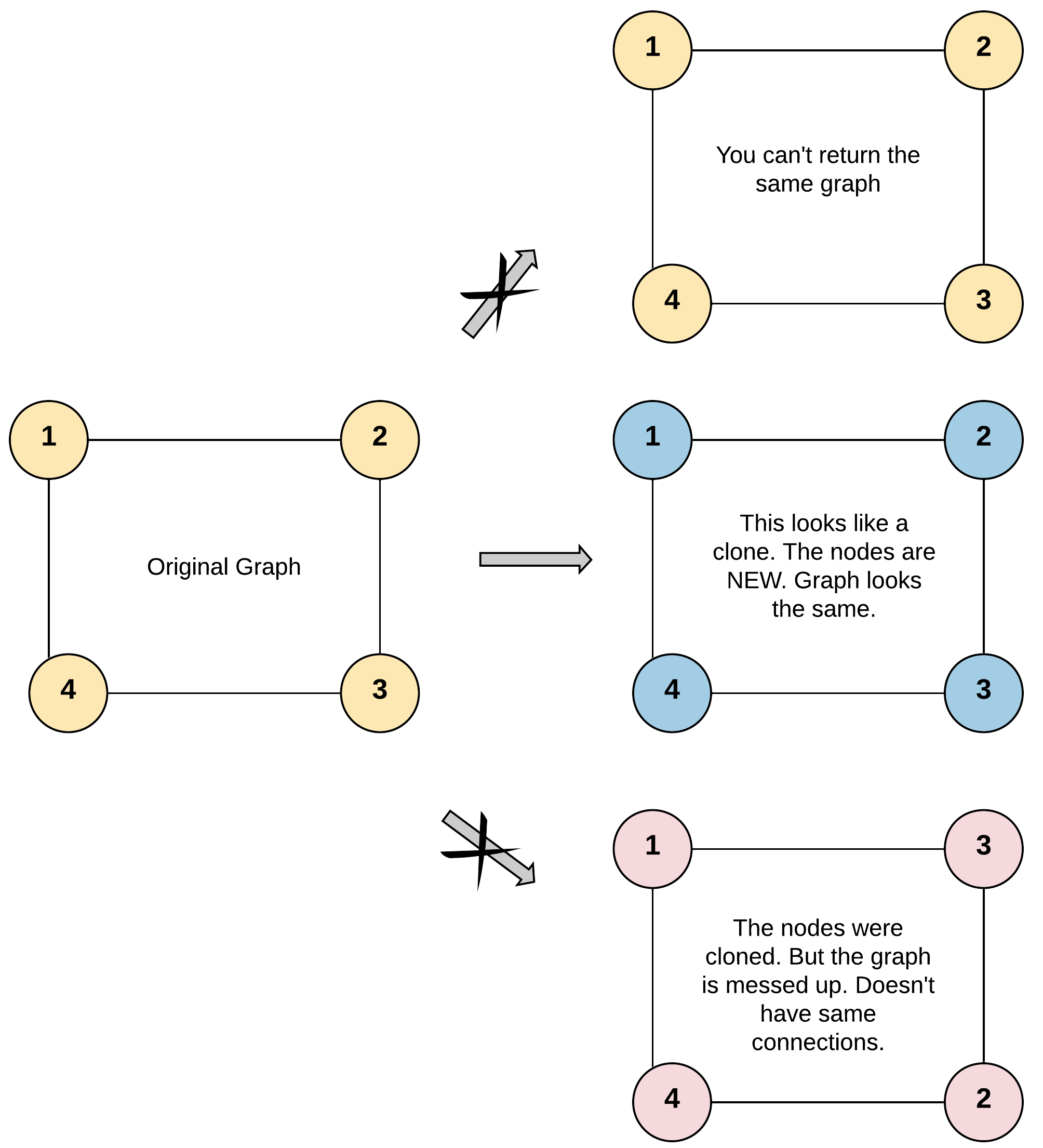
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]

输出：[[2,4],[1,3],[2,4],[1,3]]

解释：

图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

思路：

本题就是考察图的遍历，图的遍历方法有深度优先遍历(DFS)和广度优先遍历(BFS)两种方法。而关于这两种方法的复现大家想必也比较熟悉，网上也有诸多资料。此处我想讲讲如何构建本题所用的测试样例。

题目中是给出了测试样例，但是它给的是邻接列表形式，不是代码给定的Node节点正规格式。当然了，以邻接列表形式给出能更形象的表示出图，但是我们自己在做题时肯定是想着自己构建出正确的测试样例出来，这样不管是解题还是测试都会很方便。我在网上查了很多资料，结果都没有看到构建简单无向图的方法，这让我有些受挫，本着方便他人的心态，我挠破脑皮终于想到了构建测试样例的方法。

构建测试样例代码如下：

def createGraph(edges):
    """
    构建无向图
    :param edges: List[List[int]] -> 图中所有边的集合
    :return: Node -> 无向图
    """
    lookup = {}
    for edge in edges:
        if edge[0] not in lookup:
            lookup[edge[0]] = Node(edge[0])
        if edge[1] not in lookup:
            lookup[edge[1]] = Node(edge[1])
        lookup[edge[0]].neighbors.append(lookup[edge[1]])
        lookup[edge[1]].neighbors.append(lookup[edge[0]])
    return lookup[edges[0][0]]

代码并不复杂，关键就是定义出一个lookup字典来保存每个节点的相关信息，当遍历到该节点时直接取出即可。

我觉得这是本题的关键，此处解决了，后面的解题也就很快了。我用的是深度优先遍历方法，核心也是定义出一个lookup字典来保存每个节点的相关信息。

代码如下：

class Node(object):
    def __init__(self, val = 0, neighbors = []):
        self.val = val
        self.neighbors = neighbors

class Solution(object):
    def cloneGraph(self, node):
        """
        :type node: Node
        :rtype: Node
        """
        lookup = {}

        def dfs(node):
            
            if not node: return
            print(node.val)
            if node in lookup:
                return lookup[node]
            clone = Node(node.val, [])
            lookup[node] = clone
            for n in node.neighbors:
                clone.neighbors.append(dfs(n))

            return clone

        return dfs(node)

def createGraph(edges):
    """
    构建无向图
    :param edges: 图中所有边的集合
    :return: 无向图
    """
    lookup = {}
    for edge in edges:
        if edge[0] not in lookup:
            lookup[edge[0]] = Node(edge[0])
        if edge[1] not in lookup:
            lookup[edge[1]] = Node(edge[1])
        lookup[edge[0]].neighbors.append(lookup[edge[1]])
        lookup[edge[1]].neighbors.append(lookup[edge[0]])
    return lookup[edges[0][0]]


if __name__ == "__main__":
    edges = [[1, 2], [2, 3], [3, 1]]
    graph = createGraph(edges)
    print(graph)
    cloneGraph = Solution().cloneGraph(graph)
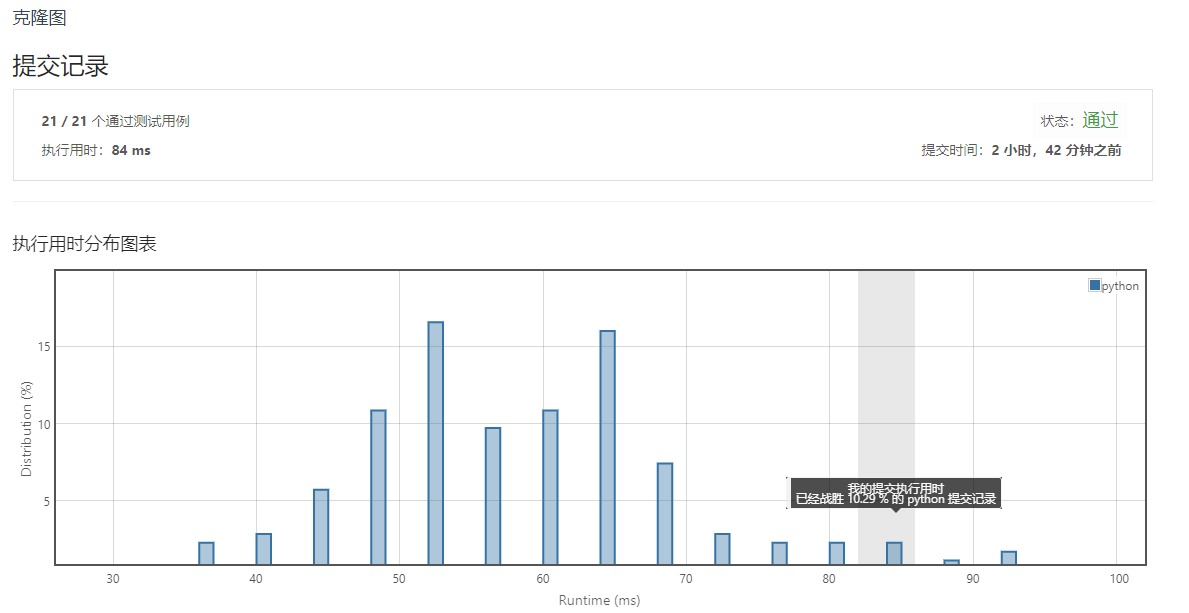
    print(cloneGraph)

执行效率相对较差，在10%左右，属实尴尬了。