简介

在工程实践中，完成一个项目，通常可以分两步走：

1. 产品实现，即完成产品的编码，实现产品需求，能够提供所需的功能；
2. 产品优化，即对产品已有功能进行优化，可以是并发度、延时、qps等各个方面的优化；

当然，也可以两步合一步走，在代码实现的同时，就将产品优化考虑进去，但实际情况，产品往往要求优先提供功能，即该产品要具有某种能力，所以开发周期比较偏短，难以将深层次代码优化一起考虑进去，实际情况一般都是快速迭代，分两步走的方式，甚至可以是实现多个功能后再一起优化。

以上也只是工作中的一些体会，并不代表所有的项目开发情况。

其中，内存缓存（cache） 是我们在进行产品优化过程中，经常会用到的一种手段，举例如下：

微信中发的一条朋友圈动态，动态内容一般都是由 图片 + 文字 的方式呈现，这些内容统统存储在后台服务器中的磁盘中，每有一个人来查看你的朋友圈动态，就需要从磁盘中读取一次，如果你是有5000好友的社交达人，那么极端情况下会有5000次 并发访问 朋友圈的情况，这时，就会出现刷新2分钟都看不到朋友圈动态的情况，你说急不急？

当然，为了防止上述情况的出现，最常用的就是通过内存缓存来进行优化了，将动态内存放到内存中，每访问一次不需要从磁盘读取，只需要从内存读取，内存的访问时间一般在ns级，磁盘的访问时间在ms级，具体时间可查阅相关资料，通过内存缓存大大降低了数据的读取延时，也就不会出现等待2分钟还刷不出来动态地情况了。

然而，内存空间总是有限的，目前无法将所有的数据全部放入内存，只能够将部分热点数据放到内存，同时，热点数据又不是一成不变的，这就会产生将已经过时的热点数据从内存淘汰，再加入新的热点数据的问题，这就是内存缓存中会遇到的淘汰问题，对于内存缓存的淘汰问题，常用的解决算法主要有以下几种：
OPT、FIFO、LRU、2Q、LIRS等等，下面主要来看下每个算法是如何实现的，又具有怎样的优缺点。

缓存淘汰算法

不可能实现的算法 OPT

OPT（OPTimal Replacement，OPT）算法，其所选择的被淘汰的数据将是以后永不使用的，或是在最长（未来）时间内不再被访问的数据。

未来发生的事情是无法预测的，所以该算法从根本上来说是无法实现的，OPT算法对于内存缓存来说，能够提供最高的cache命中（cache hite）率，通过OPT算法也可以衡量其他缓存淘汰的算法的优劣。

无脑算法 FIFO

FIFO（First Input First Output，FIFO）算法算是一种很无脑的淘汰算法，实现起来也很简单，即每次淘汰最先被缓存的数据。

FIFO算法很少会应用在实际项目中，因为该算法并未考虑数据的 “热度”，一般来说，应该是越热的数据越应该晚点淘汰出去，而FIFO算法并未考虑到这一点，所以，该算法的cache命中率一般会比较低。

常见算法 LRU

LRU（Least Recently Used，LRU）算法根据数据的历史访问记录来进行淘汰数据，其核心思想是“如果数据最近被访问过，那么将来被访问的几率也更高”。

LRU最友好的数据模型为具有时间局部性的请求队列，每访问一个已缓存的节点，就将该节点转移到队列头部，每次淘汰时，以此淘汰队列尾部节点，示意图如下：

采用队列实现的话，每转移一个节点，都需要遍历该队列，为了提高查找效率，通常会采用Hashmap+双向链表来实现LRU算法。

当存在热点数据时，LRU的缓存命中率比较高，但是由于未考虑频率因素，偶发性的、周期性的批量操作时缓存效果较差，缓存污染严重。

为了解决LRU算法未考虑频率因素的问题，人们在此基础上又提出了LRU-K算法，其中，K代表最近使用的次数，因此LRU可以认为是LRU-1算法，其核心思想是将 “最近使用过1次”的判断标准扩展为“最近使用过K次”。

相比LRU，LRU-K需要多维护一个访问历史队列，用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候，才将数据放入缓存。当需要淘汰数据时，LRU-K会淘汰第K次访问时间距当前时间最大的数据。

LRU-K算法不仅具有LRU算法的优点，而且LRU-K算法将LRU算法的“访问1次”扩展为“访问K次”，弥补了LRU算法未考虑频率因素的缺点，实际应用中LRU-2是综合各种因素后最优的选择，LRU-3或者采用更大的K值，缓存命中率会增高，但适应性会变差，因为随着K值得增大，需要大量的数据访问才能将历史访问记录清除；同时，LRU-K算法需要维护一个历史访问队列，因此内存消耗也会增加，同时，LRU-K需要将缓存队列的中元素按照访问时间排序，以方便淘汰访问时间最久的元素，所以，该算法也需要额外的O(logN)时间复杂度。

进阶算法 2Q

2Q（Two Queues）算法和LRU-2类似，不同点在于2Q将LRU-2算法中的访问历史队列改为一个FIFO缓存队列，即2Q算法有两个缓存队列：一个是FIFO队列，一个是LRU队列。

当数据第一次访问时，2Q算法将数据缓存在FIFO队列里面，当数据第二次被访问时，则将数据从FIFO队列移到LRU队列里面，两个队列各自按照自己的方法淘汰数据，示意图如下：

2Q算法和LRU-2算法缺点类似，由于维护了两个缓存队列，内存消耗会增加，但是2Q算法的时间复杂度优化到了O(1)。

和LRU-K算法类似，MQ（Muti Queue）是2Q算法的拓展算法，MQ算法将按照数据的访问频率划分成多个队列，不同的队列具有不同的访问优先级，MQ算法总数优先缓存访问次数最多的数据，随着数据的访问频率越高，其所处的队列优先级也越高，当数据从最高优先级访问队列中淘汰出去之后，会重新加入到第一级的访问队列中，以此类推。

但是MQ算法需要维护多个优先级队列以及缓存数据，内存消耗比较大。

进阶算法 LIRS

LRU算法是应用范围很广的cache淘汰算法，但是该算法存在以下几个缺点：

1. 对冷数据突发性访问抵抗能力差，可能会因此淘汰掉热的文件；
2. 对于大量数据的循环访问抵抗能力查，极端情况下可能会出现命中率0%；
3. 不能按照数据的访问概率进行淘汰；

可以说其主要缺点是第三条，其他缺点，都是由于该确定所导致的，所以，在LRU的基础上，又有了LRU-K、2Q、MQ等各种衍生算法，但是这些算法由于要多维护几个缓存队列，会消耗更多的内存资源，为了解决上述的所有问题，后面又提出了一种LIRS缓存淘汰算法。

LIRS算法中，对于每一个缓存数据块，都维护了以下两个变量来衡量数据的访问频率：IRR(Inter-Reference Recency)和R（Recency），IRR为一个数据块最近两次访问期间，有多少个不同的数据块被访问过，当数据块第一次被访问时，IRR初始化为无穷大（inf）。R为数据块最近一次访问到当前时间内有多少不同的数据块被访问过，示例如下：

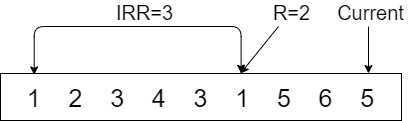
横框内为被访问的数据库标号，对于数据块1来说，两次访问期间，有2、3、4这三个不同的数据块被访问过，所以数据块1的IRR=3，此时，数据块最后一次被访问到当前时间片期间，共有5、6两个不同的数据块被访问过，所以数据块1的R=2。

LIRS算法将数据块分为LIR和HIR两级的方式，会综合比较IRR和R值来进行数据淘汰：

• LIR（Low IRR）：热数据块，具有较小的IRR值，IRR值小，说明数据的访问频率较高；
• HIR（High IRR）：冷数据库，具有较大的IRR值，IRR值较大，说明数据得到访问频率较低；

LIR块一般会常驻cache，不会进行数据淘汰，数据淘汰只发生在HIR数据块中，其中，只有部分数据是缓存在HIR中，HIR数据块又化分为resident-HIR，称为缓存中的数据块集合，和nonresident-HIR，称为未缓存的数据块集合。

内存中缓存的数据量大小为count(LIR)+count(resident-HIR)，当缓存发生未命中时，会优先淘汰resident-HIR中的数据，若缓存命中resident-HIR，则需要更新命中数据块的IRR值，若IRR值比LIR集合中最大的R值要小，则需要将LIR的数据块进行置换，举例如下：

第一列中的ABCDE代表了5个数据块，最底下一行代表数据块访问时间，x表示该数据块在某一时间点被访问，在时间点10时，数据块{A,B,C,D,E}的R值和IRR值分别为：

• R({A,B,C,D,E}) = {1,3,4,2,0}
• IRR({A,B,C,D,E}) = {1,1,inf,3,inf}

假设LIR集合的大小Lirs=2，HIR集合的大小Lhirs=1，则在时间点10，LIR和HIR集合中的数据分别为：

• LIR = {A,B}
• HIR = {C,D,E}

因为E是最后一次访问的数据块，则

• resident-HIR = {E}
• nonresident-HIR = {C,D}

若在11时间点时，再次访问了数据块E，则此时数据块{A,B,C,D,E}的R值和IRR值分别为：

• R({A,B,C,D,E}) = {1,3,4,2,0}
• IRR({A,B,C,D,E}) = {1,1,inf,3,0}

由于IRR(E) < R(B)，则需要将LIR集合与HIR集合进行数据置换，置换后的集合状态为：

• LIR = {A,E}
• HIR = {B,C,D}

因为D是HIR集合中最近一次访问的数据块，则

• resident-HIR = {D}
• nonresident-HIR = {B,C}

上面所说的数据置换操作，一定是HIR中数据的IRR值要小于LIR集合中最大的R值时，才会进行数据置换操作，而不是LIR集合中的IRR值，主要是基于以下两个原因：

1. IRR值其实是基于R值生成的，只是IRR值会落后于R值更新；
2. 基于原因1，如果HIR中的IRR值小于LIR的R值，则HIR中数据块的LIR值肯定会小于LIR数据块的下一个IRR值；

总结

LRU-K，2Q，LIRS三种算法都基于倒数第二次的访问时间，以此推断块的访问频率，从而替换出访问频率低的块。从空间额外消耗来看，除了LRU-K需要记录访问时间外，LIRS需要记录块状态（HIR/LIR等），2Q并不需要太多的访问信息记录，因此2Q>LIRS>LRU-K。从时间复杂度来看，LRU-K是O(logN)，2Q和LIRS都是O(1)，但LIRS的"栈裁剪"是平均的O(1)，因此2Q>LIRS>LRU-K。从实现复杂来看，LIRS只需要两个队列，2Q和LRU-K的完整实现都需要3个队列，因此LIRS>2Q=LRU-K。最后，LIRS是唯一参数不需要去按照实际情况进行调整（尽管仍然有LIR和HIR的cache大小参数），2Q和LRU-K都需要进行细微的参数调整，因此LIRS>2Q=LRU-K。从性能角度来看，LIRS论文看得出还是有一定的提升，LIRS>2Q>LRU-K。

参考资料

The LRU-K Page Replacement Algorithm For Database Disk Buffering
2Q: A Low Overhead High Performance Buffer Management Replacement Algorithm
LIRS: An Efficient Low Inter-reference Recency Set Replacement Policy to Improve Buffer Cache Performance
LRU-K，2Q，LIRS算法介绍与比较
cache 淘汰算法：LIRS 算法

最后

以上就是优雅指甲油为你收集整理的内存缓存（cache）常用淘汰算法简介缓存淘汰算法总结参考资料的全部内容，希望文章能够帮你解决内存缓存（cache）常用淘汰算法简介缓存淘汰算法总结参考资料所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。