1. 首页
  2. 文章中心
  3. 编译原理

编译原理实验五：对算术表达式的递归下降分析

66 阅读 0 评论
我是靠谱客的博主 无辜老虎，最近开发中收集的这篇文章主要介绍编译原理实验五：对算术表达式的递归下降分析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

实验要求

【任务介绍】根据给定的上下文无关文法，分析任意一个算术表达式的语法结构。

【输入】任意的算术表达式。

【输出】与输入对应的一颗语法树或者错误。

【题目】设计一个程序，根据给定的上下文无关文法，构造一颗语法树来表达任意一个算术表达式的语法结构。要求：

1.基础文法：

<Expr> → <Term> <Expr1> 
<Expr1> → <AddOp> <Term> <Expr1> | empty 
<Term> → <Factor> <Term1> 
<Term1> → <MulOp> <Factor> <Term1> | empty 
<Factor> → id |number | ( <Expr> ) 
<AddOp> → + | - 
<MulOp> → * | /

2.语法分析方法采用递归子程序法。

3.输入：形如x*1+2的算术表达式，有+、-、*、/ 四种运算符，运算符的优先级、结合规则和括号的用法遵循惯例，有变量、整数两种运算对象。为简化问题，变量和整数均为只含有1个字符的单词，忽略空格等非必要的字符。

4.输出：输入正确时，输出其对应的语法树，树根标记为；输入错误时，输出error。

编译环境和语言

编程语言：C++

IDE：vs 2019

实验原理分析

对于给定文法定义：

<Expr> → <Term> <Expr1> 
<Expr1> → <AddOp> <Term> <Expr1> | empty 
<Term> → <Factor> <Term1> 
<Term1> → <MulOp> <Factor> <Term1> | empty 
<Factor> → id |number | ( <Expr> ) 
<AddOp> → + | - 
<MulOp> → * | /

起始点为，因为采用的是LL(1)文法，所以需要不断左递归遍历，直到递归到终结字符，才会回溯，继续走另一条路，以此类推，直到最终回溯到。

对于LL(1)文法，即分析表不含多重定义入口的文法，换言之，直到不得不用右部表达式代替左部表达式的时候，再进行替换，形如：

<Expr> → <Expr><Term1> | <Expr><Term2>

就会导致不断的左递归而无法停止，这是因为在右部表达式的最左边，而我们又是使用的左递归，因此这就不是LL(1)文法。

程序关键部分分析

定义

string str = "";  //用来存储算术表达式
int location = 0;  //用来定位算术表达式
bool flag = true;  //用来判断该算术表达式是否合法
string tree_map[100];  //用来存储语法树
const int width = 3;  //设置间隔为3

int draw_line(int row, int num);
void string_out(string s, int row, int column);
void word_out(char ch, int row, int column);
int tree_out(string s, int row, int loc);
void print_tree();
int Expr(int row, int column);
int Expr1(int row, int column);
int Term(int row, int column);
int Term1(int row, int column);
int Factor(int row, int column);
bool AddOp(char ch);
bool MulOp(char ch);

关键部分分析

首先是draw_line(int row, int num)函数，用来画横线隔开兄弟节点，长度为num：

int draw_line(int row, int num) {  //用来画横线,隔开兄弟节点,返回下次开始的起始位置
	int n = tree_map[row].size();
	tree_map[row].append(num, '-');
	return tree_map[row].size();
}

对于string_out(string s, int row, int column)，用来将对应的数据存储到对应的位置上，首先需要判断输入的column是否与对应行数的长度相等，若不想等，则由于string数据类型的特性，必须将这中间部分填充上空格：

void string_out(string s, int row, int column) {  //用来输出字符串
	if (tree_map[row].size() < column) {  //若不等,则说明中间需要填充空格
		int n = column - tree_map[row].size();
		tree_map[row].append(n, ' ');
	}
	tree_map[row].append(s);
}

对于word_out(char ch, int row, int column)，用来存储对应的单个字符，其余与string_out(string s, int row, int column)类似：

void word_out(char ch, int row, int column) {  //用来输出单个字符
	if (tree_map[row].size() < column) {  //若不等,则说明中间需要填充空格
		int n = column - tree_map[row].size();
		tree_map[row].append(n, ' ');
	}
	tree_map[row] += ch;
}

对于tree_out(string s, int row, int loc)，因为是画竖线，为了美观，这里需要根据父节点的长度找到中点，然后填充空格和竖线，至于返回值，是为了方便处理单个字符的位置：

/**画父子节点之间的竖线,s表示父亲节点的字符,loc表示父亲节点的起始位置
* 返回值用于处理单个字符的位置
*/
int tree_out(string s, int row, int loc) {
	int n1 = s.size() / 2;
	int n2 = loc + n1 - tree_map[row].size();
	tree_map[row].append(n2, ' ');
	tree_map[row] += '|';
	return n1 + loc;
}

对于print_tree()，将tree_map数组中的数据按行输出：

void print_tree() {
	for (int i = 0; i < 100; i++) {
		if (tree_map[i].size() != 0) {
			cout << tree_map[i] << endl;
		} else break;
	}
}

然后便是根据提供的文法定义声明的函数，都是首先存储该文法的名称以及对应的竖线，再继续递归下降，其中返回值用来处理每一行画横线的长度：

int Expr(int row, int column) {
	if (flag) {
		string_out("<Expr>", row, column);
		tree_out("<Expr>", ++row, column);
		int num1 = Term(++row, column);
		column = draw_line(row, num1 + width);
		int num2 = Expr1(row, column);
		return num1 + num2 + width + 6;
	}
}

int Expr1(int row, int column) {
	if (flag) {
		string_out("<Expr1>", row, column);
		tree_out("<Expr1>", ++row, column);
		if (AddOp(str[location])) {  //若第一个字符为+或-
			location++;
			string_out("<AddOp>", ++row, column);
			int loc = tree_out("<AddOp>", row + 1, column);
			word_out(str[location - 1], row + 2, loc);
			column = draw_line(row, width);
			int num1 = Term(row, column);
			column = draw_line(row, num1 + width);
			int num2 = Expr1(row, column);
			return num1 + num2 + width * 2 + 7;
		} else {  //否则输出为empty
			string_out("empty", ++row, column);
			return 7;
		}
	}
}

int Term(int row, int column) {
	if (flag) {
		string_out("<Term>", row, column);
		tree_out("<Term>", ++row, column);
		int num1 = Factor(++row, column);
		column = draw_line(row, num1 + width);
		int num2 = Term1(row, column);
		return num1 + num2 + width + 6;
	}
}

int Term1(int row, int column) {
	if (flag) {
		string_out("<Term1>", row, column);
		tree_out("<Term1>", ++row, column);
		if (MulOp(str[location])) {  //若第一个字符为*或/
			string_out("<MulOp>", ++row, column);
			int loc = tree_out("<MulOp>", row + 1, column);
			word_out(str[location], row + 2, loc);
			location++;
			column = draw_line(row, width);
			int num1 = Factor(row, column);
			column = draw_line(row, num1 + width);
			int num2 = Term1(row, column);
			return num1 + num2 + width * 2 + 7;
		} else {  //否则输出为empty
			string_out("empty", ++row, column);
			return 7;
		}
	}
}

int Factor(int row, int column) {
	if (flag) {
		string_out("<Factor>", row++, column);
		int loc = tree_out("<Factor>", row++, column);
		if (isalpha(str[location])) {  //若是字母则为变量
			word_out(str[location], row, loc);
			location++;
			return 8;
		}
		else if (isdigit(str[location])) {  //若为数字
			word_out(str[location], row, loc);
			location++;
			return 8;
		}
		else if (str[location] == '(') {  //若为(,则需要等)
			word_out(str[location], row, loc);
			location++;
			column = draw_line(row, width);
			int num1 = Expr(row, column);
			if (str[location] != ')') {  //若一直没有),则说明该算术表达式错误
				flag = false;  
				return 0;
			}
			else {
				int loc1 = draw_line(row, num1 + width);
				word_out(str[location], row, loc1);
				location++;
				return num1 + width * 2 + 8;
			}
		}
	}
}

bool AddOp(char ch) {
	if (ch == '+' || ch == '-')return true;
	return false;
}

bool MulOp(char ch) {
	if (ch == '*' || ch == '/')return true;
	return false;
}

最后便是main()函数，首先在输入的算术表达式最后加上一个#来表示结束标志，然后启动Expr(0, 0)，其中(0, 0)即为string数组的起始位置，然后若最后一个字符为#，则说明完整遍历了整个算术表达式，便可以输出该语法树，否则直接输出Error：

int main() {
	cout << "请输入一个算术表达式:";
	cin >> str;
	str.resize(str.size() + 1);
	str[str.size() - 1] = '#';  //将#号设置为结束标志
	Expr(0, 0);
	if (str[location] == '#') {
		cout << "Correct!" << endl;
		cout << "接下来输出该算法表达式的语法树：" << endl;
		print_tree();
	}
	else cout << "Error!" << endl;
	return 0;
}

程序测试

输入数据：

1+2*（3-1）

运行结果如下：

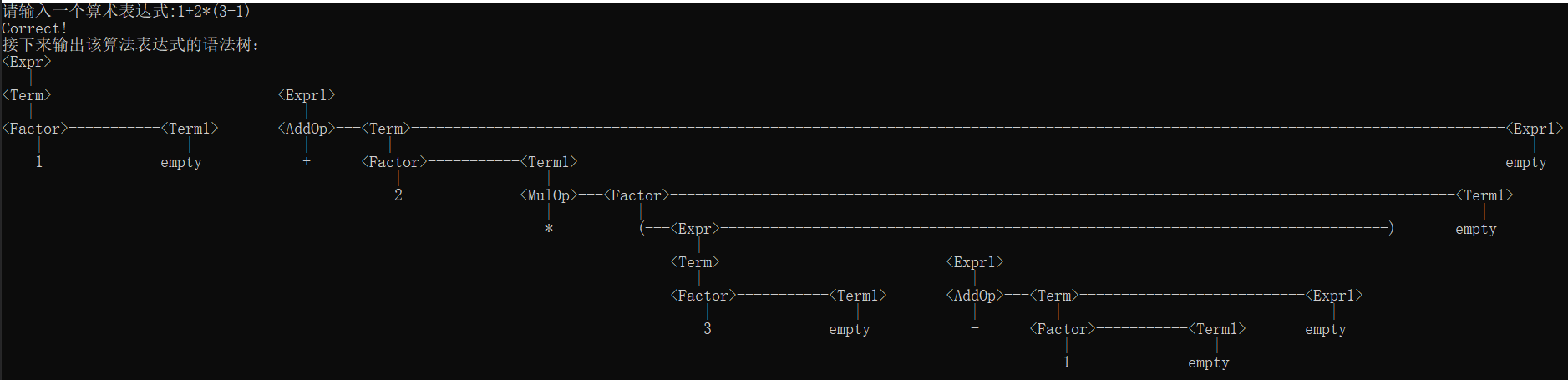
在这里插入图片描述

总结

对于构造语法树，我想到的方法是用一个string数组来存储每一行的数据，因为是递归下降，所以我的相关文法函数都是有返回值的，用来记录每一行画横线的长度，然后在不同行数记录对应的数据。

以起始点Expr文法为例：

int Expr(int row, int column) {
	if (flag) {
		string_out("<Expr>", row, column);
		tree_out("<Expr>", ++row, column);
		int num1 = Term(++row, column);
		column = draw_line(row, num1 + width);
		int num2 = Expr1(row, column);
		return num1 + num2 + width + 6;
	}
}

返回值中，num1是从Term文法得到的长度，num2是从Expr1文法得到的长度，width为Term和Expr1之间的间隔，然后6为的字符长度，如此便能够确定每次输出横线的个数以保证不会出现覆盖，但是也正因此，我的语法树的列数会非常庞大，从上面的测试用例也可以发现，仅仅只是一个很简单的算术表达式，输出的语法树的列数都已经很庞大了。

完整代码

#include<iostream>
#include<cctype>
using namespace std;

string str = "";  //用来存储算术表达式
int location = 0;  //用来定位算术表达式
bool flag = true;  //用来判断该算术表达式是否合法
string tree_map[100];  //用来存储语法树
const int width = 3;  //设置间隔为3

int draw_line(int row, int num);
void string_out(string s, int row, int column);
void word_out(char ch, int row, int column);
int tree_out(string s, int row, int loc);
void print_tree();
int Expr(int row, int column);
int Expr1(int row, int column);
int Term(int row, int column);
int Term1(int row, int column);
int Factor(int row, int column);
bool AddOp(char ch);
bool MulOp(char ch);

int draw_line(int row, int num) {  //用来画横线,隔开兄弟节点,返回下次开始的起始位置
	int n = tree_map[row].size();
	tree_map[row].append(num, '-');
	return tree_map[row].size();
}

void string_out(string s, int row, int column) {  //用来输出字符串
	if (tree_map[row].size() < column) {  //若不等,则说明中间需要填充空格
		int n = column - tree_map[row].size();
		tree_map[row].append(n, ' ');
	}
	tree_map[row].append(s);
}

void word_out(char ch, int row, int column) {  //用来输出单个字符
	if (tree_map[row].size() < column) {  //若不等,则说明中间需要填充空格
		int n = column - tree_map[row].size();
		tree_map[row].append(n, ' ');
	}
	tree_map[row] += ch;
}

/**画父子节点之间的竖线,s表示父亲节点的字符,loc表示父亲节点的起始位置
* 返回值用于处理单个字符的位置
*/
int tree_out(string s, int row, int loc) {
	int n1 = s.size() / 2;
	int n2 = loc + n1 - tree_map[row].size();
	tree_map[row].append(n2, ' ');
	tree_map[row] += '|';
	return n1 + loc;
}

void print_tree() {
	for (int i = 0; i < 100; i++) {
		if (tree_map[i].size() != 0) {
			cout << tree_map[i] << endl;
		} else break;
	}
}

int Expr(int row, int column) {
	if (flag) {
		string_out("<Expr>", row, column);
		tree_out("<Expr>", ++row, column);
		int num1 = Term(++row, column);
		column = draw_line(row, num1 + width);
		int num2 = Expr1(row, column);
		return num1 + num2 + width + 6;
	}
}

int Expr1(int row, int column) {
	if (flag) {
		string_out("<Expr1>", row, column);
		tree_out("<Expr1>", ++row, column);
		if (AddOp(str[location])) {  //若第一个字符为+或-
			location++;
			string_out("<AddOp>", ++row, column);
			int loc = tree_out("<AddOp>", row + 1, column);
			word_out(str[location - 1], row + 2, loc);
			column = draw_line(row, width);
			int num1 = Term(row, column);
			column = draw_line(row, num1 + width);
			int num2 = Expr1(row, column);
			return num1 + num2 + width * 2 + 7;
		} else {  //否则输出为empty
			string_out("empty", ++row, column);
			return 7;
		}
	}
}

int Term(int row, int column) {
	if (flag) {
		string_out("<Term>", row, column);
		tree_out("<Term>", ++row, column);
		int num1 = Factor(++row, column);
		column = draw_line(row, num1 + width);
		int num2 = Term1(row, column);
		return num1 + num2 + width + 6;
	}
}

int Term1(int row, int column) {
	if (flag) {
		string_out("<Term1>", row, column);
		tree_out("<Term1>", ++row, column);
		if (MulOp(str[location])) {  //若第一个字符为*或/
			string_out("<MulOp>", ++row, column);
			int loc = tree_out("<MulOp>", row + 1, column);
			word_out(str[location], row + 2, loc);
			location++;
			column = draw_line(row, width);
			int num1 = Factor(row, column);
			column = draw_line(row, num1 + width);
			int num2 = Term1(row, column);
			return num1 + num2 + width * 2 + 7;
		} else {  //否则输出为empty
			string_out("empty", ++row, column);
			return 7;
		}
	}
}

int Factor(int row, int column) {
	if (flag) {
		string_out("<Factor>", row++, column);
		int loc = tree_out("<Factor>", row++, column);
		if (isalpha(str[location])) {  //若是字母则为变量
			word_out(str[location], row, loc);
			location++;
			return 8;
		}
		else if (isdigit(str[location])) {  //若为数字
			word_out(str[location], row, loc);
			location++;
			return 8;
		}
		else if (str[location] == '(') {  //若为(,则需要等)
			word_out(str[location], row, loc);
			location++;
			column = draw_line(row, width);
			int num1 = Expr(row, column);
			if (str[location] != ')') {  //若一直没有),则说明该算术表达式错误
				flag = false;  
				return 0;
			}
			else {
				int loc1 = draw_line(row, num1 + width);
				word_out(str[location], row, loc1);
				location++;
				return num1 + width * 2 + 8;
			}
		}
	}
}

bool AddOp(char ch) {
	if (ch == '+' || ch == '-')return true;
	return false;
}

bool MulOp(char ch) {
	if (ch == '*' || ch == '/')return true;
	return false;
}

int main() {
	cout << "请输入一个算术表达式:";
	cin >> str;
	str.resize(str.size() + 1);
	str[str.size() - 1] = '#';  //将#号设置为结束标志
	Expr(0, 0);
	if (str[location] == '#') {
		cout << "Correct!" << endl;
		cout << "接下来输出该算法表达式的语法树：" << endl;
		print_tree();
	}
	else cout << "Error!" << endl;
	return 0;
}

最后

以上就是无辜老虎为你收集整理的编译原理实验五：对算术表达式的递归下降分析的全部内容，希望文章能够帮你解决编译原理实验五：对算术表达式的递归下降分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(44)

相关文章

【编译原理11】递归下降法分析算术表达式Problem Description
【编译原理11】递归下降法分析算术表达式Problem Description
语法分析：算术表达式递归下降分析程序设计
语法分析：算术表达式递归下降分析程序设计
递归下降法判断算术表达式的正确性 c要求主函数输入输出
递归下降法判断算术表达式的正确性 c要求主函数输入输出
编译原理学习笔记——第六讲 语法分析：自顶向下分析（递归下降分析程序）1. 构造递归下降分析器2. 扩充的巴科斯范式和语法图3. JavaCC简介
编译原理学习笔记——第六讲 语法分析：自顶向下分析（递归下降分析程序）1. 构造递归下降分析器2. 扩充的巴科斯范式和语法图3. JavaCC简介
编译原理实验五：对算术表达式的递归下降分析
编译原理实验五：对算术表达式的递归下降分析
递归下降法的语法分析器-3.1-编译原理
递归下降法的语法分析器-3.1-编译原理
编译原理语法分析器实验报告
编译原理语法分析器实验报告
【编译原理】 基于递归下降法实现语法分析器
【编译原理】 基于递归下降法实现语法分析器

评论列表共有 0 条评论

立即
投稿
返回
顶部