最接近的三数之和

问题描述

给定一个包括n个整数的数组nums和一个目标值target。找出nums中的三个整数，使得它们的和与target最接。返回这单个数的和。假定每组输入只存在唯一的答案。
例如，给定数组nums=[-1,2,1,-4],和target=-1.
与target最接近的三个数的和为2。（-1+2+1=2）

思路

暴力法

最简单的思路当然是暴力循环，将所有的三数之和求出，然后逐个比较和target的差值，最终返回差值最小的三数之和。显然这种解法时间复杂度都不是最优的。

正确思路

排序加双指针，这种思路可以有效降低时间复杂度。
首先对所有的的值进行排序，使用Arrays.sort()。然后固定一个值，双指针分别指向该值的下一个值和末尾值，然后通过三数之和和target比较调节双指针的位置，更新三数之和与target的最小差。逐个遍历固定序列中的每一个值，最终就可以得出最接近三数之和的问题。

进一步优化

以上思路是我在解题失败后，查看答案学到的思路。我的最初想法是首先要缩短序列范围，不应该将所有的数都去求和并比较，然而当我缩短序列范围之后，还是面临着要去比较三数之和和目标值的差，我采用的是暴力枚举法，不幸的是时间超时（没有达到leetcode的解题时间限制）。
但是当我看到答案之后，我马上就想到了可以采用两种思路结合的方法大大降低答案中的耗时。
也就是先将序列长度缩短，然后对缩短后的序列进行双指针法解题。事实证明我的思路是完全正确的。

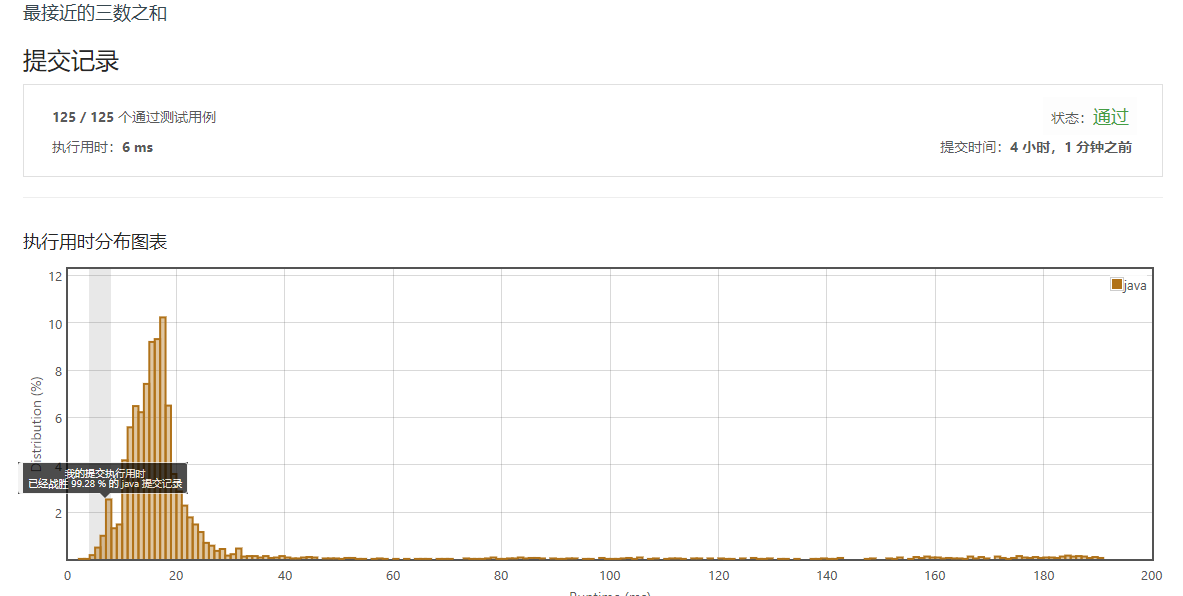
具体操作

缩减序列范围

思路如下：首先对序列排序，排序后从末端开始缩减范围，逻辑如下：

     Arrays.sort(nums);
     int l=nums.length-1;
     int i=0;
     int cha = nums[0]+nums[1]+nums[l];
     while(l>1&&cha>target) {
      l--;
      cha =nums[0]+nums[1]+nums[l];//如果最小的两个数加上nums[l]依然比target大，则说明nums[l]无法找到两个值相加等于target
     }
     if (l<nums.length-1) {
      l++;
     }
     int[] n2=Arrays.copyOfRange(nums,0,l+1);

如果最小的两个数加上nums[l]依然比target大，则说明nums[l]无法找到两个值相加等于target，那也就是说在序列排序过的情况下，我们可以放弃这些值，只保留最小的nums[l]，因为大一点也有可能和target的差最小。
同理，从首端的范围缩减思路相同：

	l=n2.length-1;
     cha =n2[0]+n2[l-1]+n2[l];
     while(i<l-1&&cha<target) {
      i++;
      cha =n2[i]+n2[l-1]+n2[l];//如果最大的两个值的和和n2[i]相加依然比target小，那么无法找到两个值之和与n2[i]相加等于target
     }
     if (i>=1)
      i--;
     int[] n3=Arrays.copyOfRange(n2,i,l+1);

如果最大的两个值的和和n2[i]相加依然比target小，那么无法找到两个值之和与n2[i]相加等于target，那么我们依然只保留最后的n2[i],之前的值全部舍弃。通过这种方式，我们从两端缩减了一大部分数值。

双指针法

之后就可以在缩减后的序列上使用双指针法：

int ans=n3[0]+n3[1]+n3[2];
     for(int t=0;t<n3.length;t++) {
      int start=t+1;
      int end=n3.length-1;
      while(start<end) {
       int sum = n3[t]+n3[start]+n3[end];
       if(Math.abs(target-ans)>Math.abs(sum-target))
        ans=sum;
       if(sum>target)
        end--;
       else if(sum<target)
        start++;
       else
        return sum;
      }
     }
     return ans;

通过以上的两种方式结合，我们实现了进一步降低解法的时间消耗。

最终代码

import java.util.Arrays;
class Solution {
    public int threeSumClosest(int[] nums, int target) {
	Arrays.sort(nums);
	int l=nums.length-1;
	int i=0;
	int cha = nums[0]+nums[1]+nums[l];
	while(l>1&&cha>target) {
		l--;
		cha =nums[0]+nums[1]+nums[l];
	     }
	if (l<nums.length-1) {
		l++;
		}
	int[] n2=Arrays.copyOfRange(nums,0,l+1);
	l=n2.length-1;
	cha =n2[0]+n2[l-1]+n2[l];
	while(i<l-1&&cha<target) {
		i++;
		cha =n2[i]+n2[l-1]+n2[l];
		}
	if (i>=1)
		i--;
	int[] n3=Arrays.copyOfRange(n2,i,l+1);
	int ans=n3[0]+n3[1]+n3[2];
	for(int t=0;t<n3.length;t++) {
		int start=t+1;
		int end=n3.length-1;
		while(start<end) {
			int sum = n3[t]+n3[start]+n3[end];	
			if(Math.abs(target-ans)>Math.abs(sum-target))
				ans=sum;
			if(sum>target)
				end--;
			else if(sum<target)
				start++;
			else
				return sum;
				}
			}
	return ans;	
	}
}
	```

最后

以上就是儒雅秋天为你收集整理的算法实现——最接近的三数之和问题求解最接近的三数之和的全部内容，希望文章能够帮你解决算法实现——最接近的三数之和问题求解最接近的三数之和所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。