第一章 绪论

计算

给出例子：绳索计算机及其算法、尺规计算机机器算法

绪论

第一节：算法

计算==信息处理：借助某种工具，遵照一定规则，以明确而机械的形式进行
所谓算法：即特定计算模型下，旨在解决特定问题的指令序列。
算法有穷性：序列的例子说明算法的有穷性。
好的算法的要求：
①简单输入，大规模输入，一般性输入，退化的输入，任意合法的输入
②能辨别不合适的输入并做适当处理，不致非正常退出
③可读性：结构化，命名，注释等
④效率：速度尽可能快，存储空间尽可能少。

实例

hailStone，学习递归算法的编写！

第二节：计算模型

<数据结构，算法> 计算–>应用

算法分析的两个方面：
①正确性：功能与问题要求是否一致；数学证明？
②成本：运行时间+所需存储空间；如何度量，比较？
考察：Ta(P)=算法A求解问题实例P的计算成本
观察：问题实例的规模往往是决定计算成本的主要因素
通常：规模接近，计算成本也接近；规模扩大，计算成本亦上升。

用算法A求解某一问题规模为n的实例，所计算的成本 T(n)
如何定义T(n):规模同为n的所有实例中，只关注最坏者，或者成本最高的。

同一问题有多种算法，如何评判其优劣？
不同的算法：程序员，语言，编译器，体系结构，操作系统，不同规模类型的输入。
解决：抽象出理想的平台或模型，不再依赖上述因素，从而准确的描述算法。

图灵机：

RAM：

T(n)：算法为求解规模为n的问题，所需要执行的基本操作次数。

第三节：大O记号

渐进分析：问题规模足够大，计算成本如何增长？
需执行的基本操作次数T(n)，需占用的存储单元数S(n) ?
big-O notation:

常系数，低次项忽略；更简洁，但依然反应前者的增长趋势。
f(n)与n的图像：

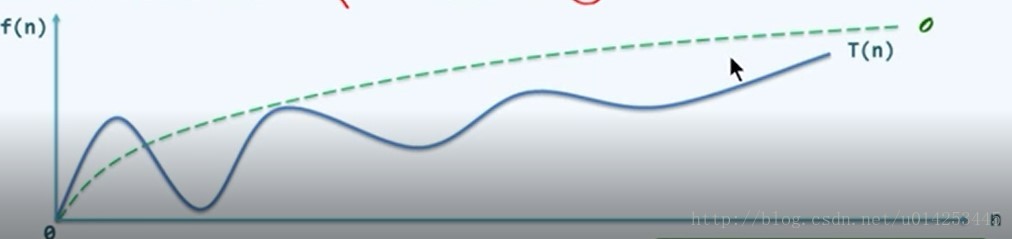
算法复杂度的意义：复杂度分级相当于无穷大的阶，反映了在规模n趋于无穷大的过程中，算法代价增长的速度。算法的复杂度，决定了一些算法是否真正能用于实际。具体使用的机器是否提供了足够多的存储，算法在实际要求的时间内能否完成。
大Ω记号，下确界。
代码段对应于常数执行时间：无循环、无分支转向、无递归调用。满足这些，执行时间就是常数O(1)

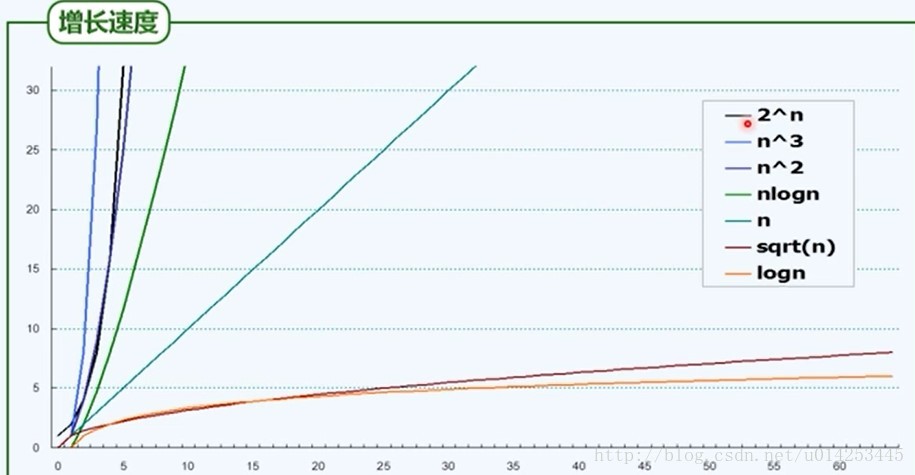
对数O(logn^C)：常底数无所谓；常数次幂无所谓；对数多项式；复杂度无限接近于常数
多项式O(N^C)：一般的取最高次幂
大部分是从O(n)到O(n^c)
指数O(2^n) T(n)=a^n

实例 2—Subset

S包含n个正整数，∑S=2m ，问是否有子集T，满足∑T=m ？ 对应美国大选选举人制是否出现同票的问题
像这样两个子集的划分问题是NPC问题。NP-complete
就目前的计算模型，不存在可在多项式时间内回答此问题的算法。

第四节 算法分析

两个主要任务：正确性(不变性 x 单调性)+复杂度
高级语言的基本指令，均等效于常数条RAM的基本指令
算法分析的目的是推导算法的复杂度，最主要技术是构造和求解递归方程
一般递归算法

def  recur(n):
     if n==0:
        return g(...)
        somework
        for i in range(a):
            x=recur(n/b)
            somework
        somework

递归方程：
T(n)=O(n^k)+a * T(n/b)

复杂度分析的主要方法
①迭代：级数求和
②递归：递归追踪+递推方程
③猜测+验证
1、算术级数：与 末项的平方，同阶。——-循环与级数：j+=2013，压缩； n^2
2、幂方级数：比 幂次 高出一阶。
3、几何级数：与 末项 同阶 2^n –> 2^n+1；——j<<=1，n
4、收敛级数：都是常数 O(1)
5、未必收敛，长度有限：调和级数–（logn） 对数级数–（nlogn）

无论输入规模多大，某算法的时间复杂度或执行时间不变。例如：取非极端元素 O(1)

实例 代码

一、冒泡排序：给定n个整数，将它们按序排列。
扫描交换：依次比较每一对相邻元素，如有必要就交换；若整次的扫描都没有进行交换，则排序完成；否则就再做一次扫描交换。

二、BOTEC back of the envelope calculation 封底估算实例

第五节 迭代和递归

数组求和的迭代：时间复杂度，空间复杂度
空间复杂度：除了输入参数，计算所需的空间
减而治之：为求解一个大规模的问题，可以将其划分为两个子问题，其一平凡，另一规模缩减，分别求解子问题，由子问题的解，得到原问题的解。

实例

数组求和：线性递归。O(n)

递归跟踪（recursion trace）分析：检查每个递归实例，累计所需时间，总和就是算法的执行时间。
利用递推方程来计算复杂度T(n)
数组倒置：任给A[0,n]将其前后颠倒
二分递归：T(n)=各层递归实例所需时间之和

max2，求最大的两个下标：求出最大值，然后由该下标作为下标界点，除去后分两部分找下一个最大值；取左部分的最大值，与右部分比较。无论如何比较，总的比较次数是 ( 2n-3 )
递归+迭代

动态规划

一、fib()递归

递归跟踪来查看复杂度
fib()递归版的低效在于，各递归实例均被大量重复的调用。
解决方法A：（记忆：memoization）
将已计算过实例的结果制表备查
解决方法B：（动态规划：dynamic programming）
颠倒计算方向：自顶而下递归，为自底而上迭代
二、LCS递归
子序列：由序列中若干字符，按原相对次序构成
最长公共子序列：两个序列公共子序列中的最长者
对于序列A[0,n]和B[0,m]，LCS(A,B) 无非三种结果
0）若n= -1 或 m= -1 则取作空序列（”“）
1）若A[n]=’X’=B[m], 则取作LCS( A[0,n),B[0,m) )+ ‘X’ 减而治之
2）若A[n]≠ B[m],则在 LCS( A[0,n],B[0,m) ) 与 LCS( A[0,n),B[0,m] )中取更长者。
单调性：无论如何，每经过一次比对，原问题的规模必可减小；具体的，作为输入的两个序列，至少其一的长度缩短一个单位。
最好情况(不出现第2种情况)下，原问题将分解为两个子问题，在随后进一步导出的子问题，可能雷同。

补充python数据结构与算法

1）python中各种组合数据对象都没有预设最大元素个数，根据元素个数增长自动扩充存储空间；即时再删除元素，表占用的存储空间也不会再变小。
2）python的自动存储管理系统。全局变量，这个值始终占用存储空间；但当被赋值或者局部变量，表对象可以被回收。
python容易构造，通常也容易写错误的程序，开销太大，生成大量不必要的数据对象。应该关注程序的空间和时间开销。
python这样的编程系统提供了许多非常有用的高级功能，但是要想有效的使用，有必要了解数据结构的深入情况！

一些典型的数据结构：

集合结构：把一组数据包装为一个整体，最简单的一类数据结构。
序列结构：元素明确的先后关系，线性，有方向性。
层次结构：数据元素分属不同层次，上层元素可以关联着一个或者多个下层元素。
树形结构：层次结构中最简单的一种关系。根，下层元素。
图结构：数据结构元素之间可以任意复杂相互联系。
也可认为图结构包含了前面几类结构，把那些结构看作图的受限形式。
算法和程序中的数据结构：
结构性和功能性的数据结构：栈，队列，优先队列，字典等
在计算机内存里表示数据元素之间的联系：
①利用数据元素的存储位置隐式表示；序列中元素线性关系。
②把数据元素之间联系也看做一种数据，显示存储内存中。

python变量和对象
几个标准数据类型：list，tuple，dict等！

最后

以上就是年轻保温杯为你收集整理的第一章 绪论的全部内容，希望文章能够帮你解决第一章 绪论所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。