Leetcode 刷题笔记：哈希表篇

基本概念

哈希表：根据关键码的值而直接进行访问的数据结构

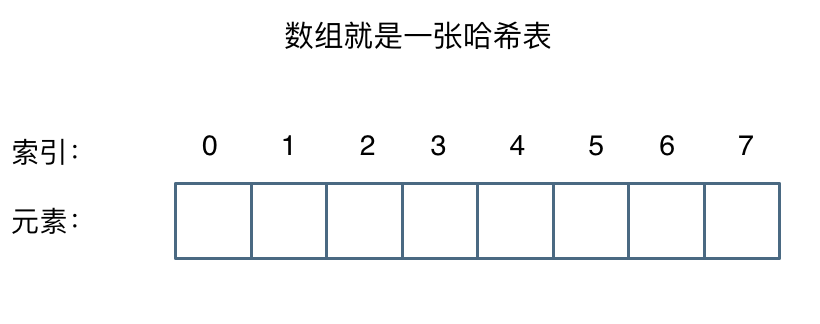
那么哈希表能解决什么问题呢，一般哈希表都是用来快速判断一个元素是否出现集合里。 

哈希函数：

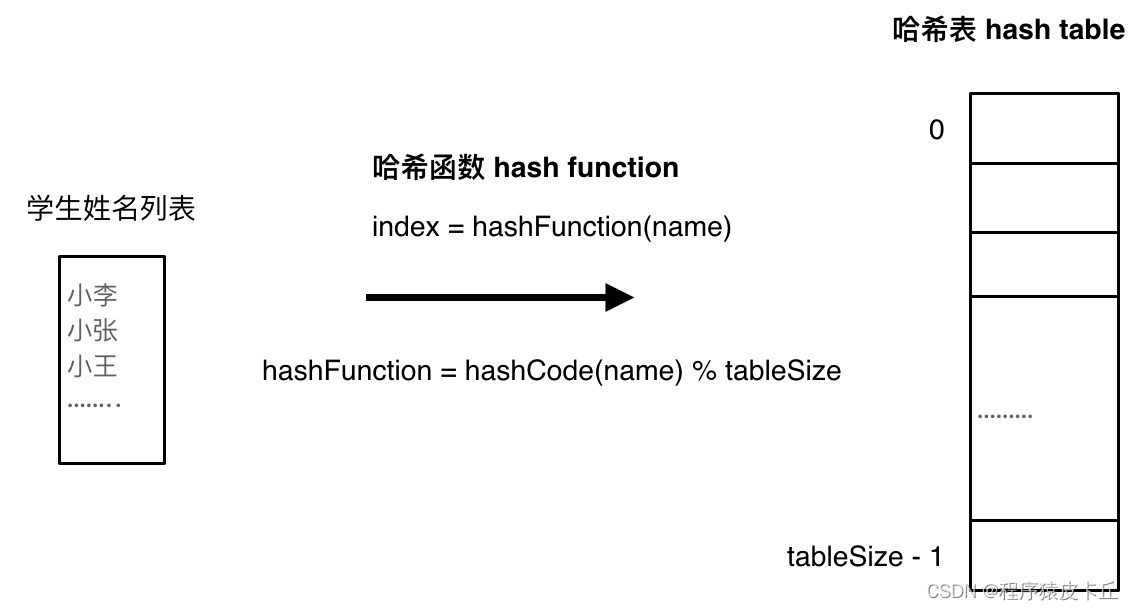
 哈希碰撞：

一般哈希碰撞有两种解决方法， 拉链法和线性探测法。

 

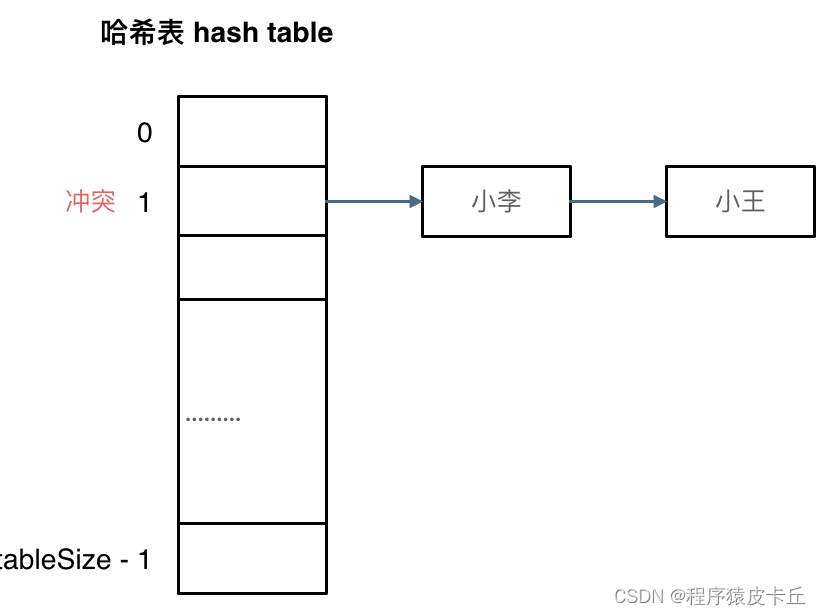
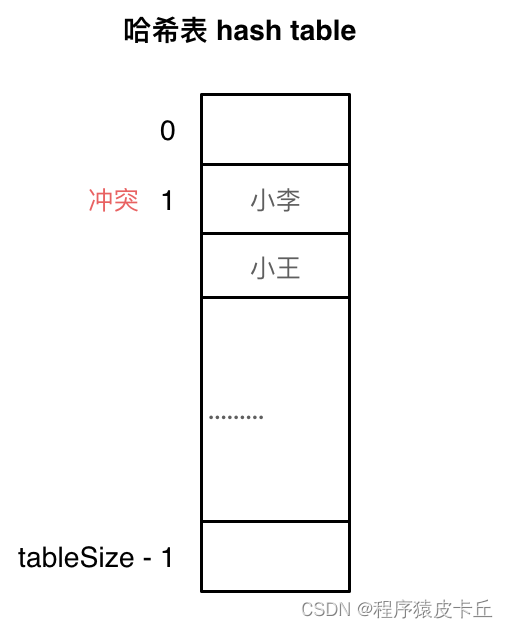
常见的三种哈希结构：

数组array，集合set，映射map。

在C++中，set 和 map 分别提供以下三种数据结构，其底层实现以及优劣如下表所示：

集合	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::set	红黑树	有序	否	否	O(log n)	O(log n)
std::multiset	红黑树	有序	是	否	O(logn)	O(logn)
std::unordered_set	哈希表	无序	否	否	O(1)	O(1)

std::unordered_set底层实现为哈希表，std::set 和std::multiset 的底层实现是红黑树，红黑树是一种平衡二叉搜索树，所以key值是有序的，但key不可以修改，改动key值会导致整棵树的错乱，所以只能删除和增加。

映射	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::map	红黑树	key有序	key不可重复	key不可修改	O(logn)	O(logn)
std::multimap	红黑树	key有序	key可重复	key不可修改	O(log n)	O(log n)
std::unordered_map	哈希表	key无序	key不可重复	key不可修改	O(1)	O(1)

std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底层实现是红黑树。同理，std::map 和std::multimap 的key也是有序的（这个问题也经常作为面试题，考察对语言容器底层的理解）。

当我们要使用集合来解决哈希问题的时候，优先使用unordered_set，因为它的查询和增删效率是最优的，如果需要集合是有序的，那么就用set，如果要求不仅有序还要有重复数据的话，那么就用multiset。

那么再来看一下map ，在map 是一个key value 的数据结构，map中，对key是有限制，对value没有限制的，因为key的存储方式使用红黑树实现的。

虽然std::set、std::multiset 的底层实现是红黑树，不是哈希表，但是std::set、std::multiset 依然使用哈希函数来做映射，只不过底层的符号表使用了红黑树来存储数据，所以使用这些数据结构来解决映射问题的方法，我们依然称之为哈希法。 map也是一样的道理。

这里在说一下，一些C++的经典书籍上 例如STL源码剖析，说到了hash_set hash_map，这个与unordered_set，unordered_map又有什么关系呢？

实际上功能都是一样一样的， 但是unordered_set在C++11的时候被引入标准库了，而hash_set并没有，所以建议还是使用unordered_set比较好，这就好比一个是官方认证的，hash_set，hash_map 是C++11标准之前民间高手自发造的轮子。

---

1. Leetcode 242 有效的字母异位词（题解）

难度：⭐️

这道题目比较简单，就是创建一个哈希表，先遍历s并记录到表中（键值+1），然后遍历t，检查每个元素是否在表中，如果不在返回false，如果在，键值-1。最后遍历一遍哈希表，如果有键值不为0的情况，返回false，否则返回true。具体代码。时间复杂度O(k)，空间复杂度O(26)。（当k足够大时，键最多有26种情况）

这道题目也可以用数组来写（因为已知索引范围）。具体代码。数组相比哈希表而言，在索引范围确定且较小时，效率更高。（因为不需要每次通过计算哈希函数来确定索引，且哈希表一开始申请空间的效率远低于数组）

另外一种解法是先对两个string排序，然后判断是否相等。具体代码。时间复杂度O(klogk)，空间复杂度O(logk)。这里解释一下，快速排序的每次调用时，只需要O(1)的空间，但递归调用栈的平均深度是logn（最坏情况n），所以在一般情况下，空间复杂度是O(logk)。

有一点值得注意的是，数组（哈希表）方法虽然时间复杂度看起来更低，其实是O(k+26)，当实例中如果k<<26时，k+26不见得比klogk要快。当然，如果k足够大，O(k+26)=O(k)。

---

2.Leetcode 49字母异位词分组

难度：⭐️⭐️⭐️

这道题的核心思想，是使用哈希表的键来存储每一种异位词anagram，用值来存储这种异位词所有的字符串（vector<string>）。具体存储键时，有两种方式：

1.排序：遍历每个输入字符串，并将其排序后新字符串，作为键。如果已在哈希表中，则更新键值，否则新创建一个键。这种方式的时间复杂度为O(nklogk)，空间复杂度为O(nk)。具体代码。

2.计数：遍历每个输入字符串，统计各个字符出现个数，将其拼成字符串返回，作为键。这种方式时间复杂度降低为O(n*(k+26))，空间复杂度O(nk+26c), c为哈希表中键的个数，O(26)代表键的长度，当n和k都足够大时，可忽略26c，时间复杂度为O(nk)，空间复杂度为O(nk)。具体代码。

我一开始没有想到用哈希表来存储，而是直接建了一个二维向量vector<vector<string>> res，然后每次遍历输入字符串时，再遍历一次这个二维向量中第一维中的每个元素的第一个值res[i][0]，将其与输入值strs[n]比较，如果和已有的异位词相同，则res[i].push_back(strs[n])，否则res.push_back(vector<string>({strs[n]}))。我分别用计数和排序来实现，前者时间复杂度O(n2*(k+26))，后者O(nklogk+n2k)，前者空间复杂度为O(26)，后者O(k)。我这里之所以写成O(26)而不是O(1)，因为很多实际情况下，k比26还要小。

我的这种方法，空间复杂度少了O(n)，但代价是时间复杂度多了O(n)倍。实际运行时，排序勉强通过，计数直接超时。

// 其实我这种方法，把二维向量当作哈希表，相当于每次都手动遍历了一遍哈希表中所有的键res[i]（时间复杂度O(n)），而非像原有哈希表那样，直接通过哈希函数找到键res[i]的索引位置（时间复杂度O(1)）。这也就是我的方法时间复杂度多了O(n)的原因。

---

3.Leetcode 438 找到字符串中所有字母异位词

难度：⭐️⭐️⭐️

这道题目用到了滑动窗口的思想，首先建立一个数组来统计字符串p中各个字符的出现个数（遍历字符串，将数组中对应字符位置的值+1），然后取p.size()作为s中滑动窗口的大小，完成滑动窗口的初始化（遍历窗口中每个元素，将数组中对应字符位置的值-1）。接下来便可以滑动窗口来遍历s了，每次先判断当前窗口是否已构成异位词（数组中各个字符索引的值为0），如果是，则将窗口起始位置索引加入到结果vector<int> res中。然后将窗口向右移动一个字符长度，直到滑动窗口末端到s.size()-1的位置停止。具体代码。

这个方法的时间复杂度为O(p+(s-p)*min(p,26)),其中s和p为字符串s和p的长度，在每次滑动窗口判断异位词时：a)我们可以遍历整个数组索引，判断每个索引的值是否为0，b)也可以直接遍历p中每个字符，查看其在数组中对应索引中的值是否为0（每次滑动窗口后的异位词判定，只需判断p出现过的字符在数组中对应索引的值是否为0，并不需要关注数组中p没出现过的字符，因为窗口的长度等于p的长度，一旦窗口中包含p没有的字符，那么数组中必有p中某个字符对应的索引值不为0）。具体采用哪种方法，取决于p和26的相对大小，因此这里复杂度用的是min(p,26)。空间复杂度为O(26)。

采用数组的方法，每次滑动窗口移动过程中，判定异位词的遍历过程，进行了一些不必要的操作（如：采用遍历整个数组的方法，遍历了数组中p中没出现字符的值；采用遍历字符串p的方法，多次遍历了数组中p的重复字符的值）

一种改进方法，是将数组替换为哈希表。这样只会记录p中出现过的字符的个数，每次滑动窗口时，如果新加入窗口的字符不在哈希表中，可直接忽略，判定异位词时，也只需要遍历哈希表中的每个键，而不需要遍历整个数组或者整个字符串p。具体实现代码。

这种方法的时间复杂度O(p+(s-p)*c),其中c为字符串p中字符种类数。空间复杂度为O(c)。

看了官方题解后，发现还有一种改进方法，可以将每次滑动窗口判定异位词的时间复杂度从O(min(26, p))或者O(c)降低至O(1)。具体思想就是建立一个整形变量dif,记录哈希表中键值不为0的个数。在初始化滑动窗口时，初始化dif的值，然后每次滑动窗口时，只需要判定一下更新后的窗口两端，是否会改变了dif的值。这样每次只需要判断dif是否为0，就知道是否为异位词了，而不需要再去遍历数组/哈希表。

这种方法的时间复杂度O(p+p+c+(s-p))=O(s+p+c)，空间复杂度为O(c)。

---

4. Leetcode 349两个数组的交集（题解）

难度：⭐️

这道题目比较简单，直接建立两个哈希表unordered_set，分别统计nums1和nums2的数字种类，然后遍历两个表，返回共同的键即可。具体代码。时间复杂度O(m+n)，空间复杂度O(m+n)

优化版本是只使用一个哈希表unordered_set来统计nums1，然后用另外一个unordered_set来保存结果，然后遍历nums2，找到相同数字便写入到结果set中，最后返回答案。具体代码。注意代码中直接调用了构造函数(iter::begin(), iter::end())，将vector初始化为set，或将set初始化为vector。

本题也可以使用数组来解答（因为题目限定了nums中数组的大小范围[1,1000]，所以我们可以建立一个int arr[1000]。具体代码。时间复杂度O(m+n)，空间复杂度O(1000)

本题还有一种做法是排序+双指针，先将两个数组排序，然后用两个指针分别指向数组头部，然后依次遍历并比较两个指针元素值大小，小的一个指针向右移动一位，如果相等，且不等于pre（用于保存上次相等值），则插入结果set，同时更新pre，及两个指针同时向后移动一位，当一个指针越界后，停止遍历。这个方法返回的结果，是已经排序后的答案。具体代码。该方法的时间复杂度O(nlogn+mlogm)，空间复杂度，位快速排序递归层数需要的栈空间。

Tips:什么时候适合用数组or哈希表？

答：使用数组来做哈希的题目，题目都限制了数值的大小。如242有效的字母异位词。

直接使用set 不仅占用空间比数组大，而且速度要比数组慢，set把数值映射到key上都要做hash计算的。不要小瞧这个耗时，在数据量大的情况，差距是很明显的。

但如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。

所以具体使用哪种方式更优，要根据具体实际情况来定。

---

5.Leetcode 350两个数组的交集II

难度：⭐️

这道题算是上道题的一个变体，要求返回全部交集（含重复），所以采用一个哈希表unorder_map来计算nums1中各数字出现的次数，然后遍历nums2各数字，每当在哈希表中找到且次数>0时，将其插入到待返回值vector中，同时次数-1。具体代码。时间复杂度O(m+n)，空间复杂度O(min(m,n))。

一个小的优化细节，首先判断nums1和nums2的长度，将小的数组插入到哈希表中，这样便可以将空间复杂度由O(m+n)降低到O(min(m,n))。

和上道题同理，本题也可以采用排序+双指针的方法，不过更推荐哈希表方法，效率更高。

---

6.Leetcode 202 快乐数（题解）

难度：⭐️⭐️

这道题本身并不算难，分析时间复杂度/空间复杂度却相当困难，下面分别来进行说明。

首先本题可以拆解成两部分：1.找到下一个数字findnext() 2.判断是否为快乐数。这里主要讨论第二部分的实现方法。

方法一：哈希表

将每次findnext(n)的结果计入哈希表中，然后将其值赋给n，继续循环，直到n==1或者set.find(n)!=set.end()为止。具体实现代码。

关于复杂度分析，可详见官方题解。对于任意一个数n，计算findnext()的时间复杂度为O(logn)。当n很大时，findnext(n)的结果会远小于n。值得一提的是，findnext(999)=243，所以当n<243后，findnext(n)的值永远不会超过243，所以进入循环前最多会再遍历243次，每次调用findnext()时间复杂度最大为3.

因此，该方法时间复杂度O(243*3+logn+loglogn+…)=O(logn)，空间复杂度O(logn)，即存放n本身需要的内存空间大小，可通过去掉前面较大（>243）的几个数，将空间复杂度降至O(1)。

//这里我其实有点小疑问，本题的logn是10为底的，考虑到n的大小范围，O(logn)甚至比O(243*3)还要小，那这种情况下，时间复杂度是够应该以O(243)为主呢？

方法二：双指针

可将本问题看作判断链表中是否有环。因此可以设置两个指针，快指针每次2步fastIndex=findnext(findnext(fastIndex))，慢指针每次1步slowIndex=findnext(slowIndex)。当fastIndex==1或fastIndex==slowIndex时，结束循环。具体实现代码。

时间复杂度最坏情况为遍历到最后为1（或出现循环），因此类似于方法一，时间复杂度为O(logn)，由于只用了两个指针，空间复杂度为O(1)。

方法三：散列表

可以通过数学分析+暴力解法得出，所有可能的循环情况，都会包含以下这一种循环形式：4→16→37→58→89→145→42→20→4，因此，可建立一个散列表来存放这几个值，每次计算findnext()时，只需判断结果值是否在这个散列表中，这样就不用将每个计算到的值都插入哈希表中，相比方法一大大节省了空间。具体实现代码。

本方法时间复杂度O(logn)，空间复杂度O(1)。

---

7.Leetcode 1两数之和（题解）

难度：⭐️

终于刷到第一题了。在前面已经做了哈希表的几道题后，对这道题的解法又有了新的认知。

首先想到的是暴力解法，两层for循环，时间复杂度O(n2)，空间复杂度O(1)。具体代码。

接下来我们就应该想到使用哈希表了。

因为我们不仅要知道元素有没有遍历过，还有知道这个元素对应的下标，需要使用 key value结构来存放，key来存元素，value来存下标，那么使用map正合适。

再来看一下使用数组和set来做哈希法的局限。

• 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。
• set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x 和 y的下标。所以set 也不能用。

此时就要选择另一种数据结构：map ，map是一种key value的存储结构，可以用key保存数值，用value在保存数值所在的下标。

接下来如何用哈希表来实现呢？我首先想到的思路是，先遍历一遍整个数组，将每个元素的值和数组索引作为键值对加入哈希表中。然后遍历整个哈希表for(auto m:map)，直到找到target-m.first值，返回其对应的索引以及m的索引即可。

但这样写的话有一个问题，如果遇到重复元素，如何处理其在哈希表中值呢？我的想法是用multimap来实现重复值的存入，每次查找时，用multimap::equal_range(target-m.first)来返回一个区间[lower_bound, upper_bound)，前者为第一个>=target-m.first的元素迭代器，后者为第一个>target-m.first的元素迭代器。这样只要lower_bound!=upper_bound，且lower_bound->second!=m.second || (lower_bound++!= upper_bound &&(lower_bound++)->second!=m.second)，则表明找到了一个不等于m自身的迭代器。返回{m.second, lower_bound(或lower_bound++)->second}即可。这种方法的时间复杂度O(nlogn)，空间复杂度O(n)。具体代码。

可以看到，multi_map虽然解决了重复元素问题，但对每个键进行了排序，造成了额外的时间开销。有没有更好的方法呢？

用unordered_multimap可以省去排序的过程，时间复杂度为O(n)，空间复杂度为O(n)。但是目前的方法都是先对整个数组全部遍历后再进行查找，有没有更简单的方法呢，比如在遍历的同时进行查找是否可行？

如果用unordered_map，如何解决重复元素的统计问题呢？

一个巧妙的思路是，只在哈希表中存放已遍历过的元素。这样只需要遍历一次数组，每次遍历到数组元素arr时，先查找是否target-arr值已在哈希表中，如果有的话，直接返回结果，否则将其值和索引插入哈希表。这样也就避免了重复值插入哈希表的情况出现。而且也不用将所有元素都存入哈希表，节省了时间和空间开销。时间复杂度O(n)，空间复杂度O(n)。具体代码。

此外，这种方法还可以保证每次找到的结果（索引对）不会重复，因为其中一个索引为刚遍历到的新数组索引。这在需要返回全部结果的问题中，会很有帮助。

那么干脆将本题扩展一下，如果需要返回全部结果，该如何实现呢？

还是上文提到的两个思路：

1. 用multimap，每次找到target-m.first后，用迭代器iter遍历[lower_bound, upper_bound)中所有不等于m的键值对（iter->second!=m.second），并在m.second<iter.second时（避免索引对重复），将其保存到结果中。时间复杂度平均情况O(nlogn)，最坏情况O(n2)，比如[1,1,1,1,1] target=2。每次查找时，需要遍历整个哈希表o(n)，而一般情况下这里只需要o(1)。空间复杂度O(n)。具体实现代码。

当然，也可以用unordered_multimap来实现，具体思路同上，时间复杂度平均情况为O(n)，最坏情况为O(n2)，空间复杂度为O(n)。具体实现代码。

此外，得益于multimap对键值的排序，我们也可以直接用双指针的思想，直接遍历一次哈希表得到结果，而不用根据每次遍历的值去查找哈希表中匹配的另一个值。具体思路如下：令iter1=multimap.begin(), iter2=multimap.end()--，分别向中间遍历，如果两数和iter1->first+iter2->first<target，则iter1++，如果>target，则iter2--，如果==target，则将索引对按从小到大的顺序保存到结果向量vector<vector<int>> res中。同时iter1++, iter2--。直到iter1==iter2时结束遍历。（这里有个小细节，multimap::iterator是bidirectional iterator而不是random access iterator，所以不能用iter1-1，或者iter1<iter2这样的运算符。所以在循环结束条件判定时，要格外注意写法）。具体实现代码。

2.用unordered_map<int, vector<int>>，首先完整遍历一遍数组，将相同数组元素值的索引保存在vector<int>中，接着再遍历一遍数组（只需遍历nums[i]<=target/2，即一半的部分，因为另一半一定能匹配到，这样也可以避免重复的索引对），每次找到target-nums[i]值时，分别遍历map[nums[i]]和map[target-nums[i]]的vector<int>中所有保存的索引的值，两两匹配并保存在结果向量中。（注意一种特殊情况，当两数相等时，map[nums[i]指向的是同样的vector<int>，注意索引对去重问题）正如上文提到的，这种方法基本不用进行重复判定，时间复杂度也更佳，应该更优考虑。时间复杂度平均情况O(n)，最坏情况O(n2)，空间复杂度O(n)。具体实现代码。

---

8.Leetcode 454四数相加II（题解）

难度：⭐️⭐️⭐️

这道题将输入数组增加为4个，但相比上一题取同一个数组中的两个元素，本题每个数组中的元素相互独立，所以不用考虑索引重复（自身或相互重复）的问题。

用暴力解法时间复杂度O(n4)，空间复杂度O(1)，时间显然代价太大。我自己想到的思路是，先将两个数组中的元素nums1[i]和nums[j]的和sum1存到一个哈希表中，然后计算另外两个数组nums3和nums4中元素的和sum2，然后查找-sum2是否在哈希表中，如果在，统计其出现的次数并添加到结果count中。

那么究竟用哪种哈希表结构实现呢？

因为两数和会有重复值，所以我一开始想到的思路是multiset，用键来保存前两个数组中各元素之和，然而这种方法进行了不必要的排序（多了O(logn)复杂度），同时在之后查找哈希表中元素出现次数时，还需要对equal_range返回的区间进行遍历，来计算重复个数count，极端情况下（如表中各元素相同）遍历的复杂度高达O(n2)。因此，这种方法的平均时间复杂度O(n2logn)，最坏时间复杂度O(n4)，空间复杂度为O(n2)。具体代码。

那么有没有更好的统计重复键出现个数的方法呢？答案是有的。我们可以使用unordered_map，因为本题不需要返回索引位置，所以键值对的第二个元素（value），我们可以用来存放两数和出现的个数。这样当我们之后遍历哈希表时，对于重复的键值，可以直接获得其出现的个数，并添加到返回值count中，而不需要像multiset那样遍历区间来统计个数。此外，unordered_map也避免了对键排序产生的不必要的时间复杂度。这种方法的时间复杂度为O(n2)，空间复杂度为O(n2)。具体代码。

反思了一下这两道题，我都是一开始用的multiset而没想到unordered_map，主要是没想清楚map的value应该存放什么（上题存放索引，本题存放重复个数）。在后面的题目中，应该多发散一下思考问题的方式。

---

9.Leetcode 383赎金信（题解）

难度：⭐️

这道题很简单，直接用数组或者哈希表unordered_map可解。时间复杂度O(n)。哈希表空间复杂度O(c)，数组空间复杂度O(26)，c为magazine中出现的字符种类数。由于本题最多只需要统计26个字符，使用数组避免了反复计算hash函数的开销，效率更高一些。

一些同学可能想，用数组干啥，都用map完事了，其实在本题的情况下，使用map的空间消耗要比数组大一些的，因为map要维护红黑树或者哈希表，而且还要做哈希函数，是费时的！数据量大的话就能体现出来差别了。 所以数组更加简单直接有效！

补充一个暴力解法的思路：遍历ransom中的每个字符，找到magazine中相同的字符，则erase该字符，如果没找到则返回false，否则遍历结束返回true。时间复杂度O(n3)，空间复杂度O(1)。

---

10.Leetcode 15三数之和（题解）

难度：⭐️⭐️⭐️⭐️

这道题算是难度较大的一道题目了，首先按照之前的思路，用哈希表解答，但发现非常困难。难点在于三元组的去重。我们在两数之和那道题目的扩展讨论中，返回了数组中所有和为0的索引对，那时也只需要进行索引去重。而这道题目要求返回值三元组，因此还需要进行值去重。

我的思路是建立两张哈希表，先索引去重，找到所有和为0的索引三元组，然后在此基础上，再对数值去重。a)首先用unordered_map<int, vector<int>>记录第一个数的值和对应的索引数组，然后用两层for循环遍历第二三个数j,k（循环初始条件可保证j<k），然后在哈希表查找-(j+k)的值对应的索引组，从返回的索引数组中，找到index<j的索引，组成三元组(index, j ,k)。b)对于每个索引不重复的三元组，还要判值三元组是否重复，于是用另一个unordered_map<string,vector<int>>来去重复。首先将nums[index], nums[j], nums[k]的值按从小到大排序，然后中间加上#（如：1#5#8）形成字符串，作为键，再检查哈希表中是否有相同的键，如果没有，则将三元组{1,5,8}作为键的值，加入哈希表中，这样便可以保证哈希表中每个键值的三元组不重复。具体代码。这种方法的时间复杂度O(n3)，运行时还是会提示超时。

题解的哈希表做法，时间复杂度为O(n2)，反思了一下，这道题不像Leetcode 1两数之和，并没有要求返回索引三元组，只需要返回值三元组。也就是说数组中原本的元素排列（索引顺序）并不重要，于是我们便可以先对数组进行排序，这样有利于我们后面进行值去重。我们只需要保证排序后的新数组中，满足题目条件要求的索引三元组不重复即可（比如可以在循环时，控制三个相加数的索引大小为递增顺序，即可完成索引去重）

索引去重的具体思想是，首先用一层for循环i，遍历第一个相加数nums[i]，接下来的一层循环，就转换为两数之和问题了，即[i+1,nums.size()-1]区间里，求解两数之和为-nums[i]的所有不重复的索引。我们可以从i+1开始for循环j，将已经访问过的数组元素（作为第二个相加数）放入哈希表，每次遍历j时（第三个相加数），判断-(nums[i]+num[j])是否在哈希表中，如果找到，则将值三元组{nums[i], -(nums[i]+nums[j]), nums[j]}插入到结果向量res中。在这个过程中，由于数组nums已被排序，找到的第二个相加数-(nums[i]+nums[j])肯定比还没加入哈希表的第三个相加数nums[j]索引更小，所以值三元组对应的索引三元组，一定是单调递增的。这也就保证了整个循环遍历过程中，找到的三元组索引不会重复。（如果还不理解的话，你可以把这种思想类比成暴力解法的三层for循环，每次找到的三元组索引，一定满足i<j<k）

值去重的具体思想，由于数组已经按照顺序排列，我们得到的每个值三元组（三个相加数）一定是单调递增的（不会出现[-1,0,1], [0,-1,1]这样的重复），因此我们只需要保证三个相加数自身不重复即可，第一个相加数去重的判定，当i>0时，如果nums[i]!=nums[i-1]，则continue。可以这样理解：假设这两个数相等，那么nums[i]可能组成的所有值三元组，相比nums[i-1]，就少了{nums[i-1], nums[i], -(nums[i-1]+nums[i])}这种情况，而这种情况在遍历nums[i-1]时就已经考虑，所以nums[i-1]包含了nums[i]的全部可能的三元组。

第二、三个相加数去重的判定，有两种方案。

先说下我自己的解法（详细注释代码）。首先在unordered_set中，键唯一，这样我们就已经保证了第二个相加数不重复存入哈希表。重点是第三个数，当遍历j时，如果在哈希表中找到了第二个数，则将值三元组{nums[i], -(nums[i]+nums[j]), nums[j]}加入到结果向量res中。如果后续遍历的nums[j+1]==nums[j]，就应该直接跳过，不会重复加入res。因此，我们需要设置一个int变量cur_val，来保存最后一次加入结果向量时nums[j]的值，这样后续如果nums[j+1]==cur_val，就忽略res.push_back操作。

再说下题解（具体代码）的方法，感觉没有我的直观。题解的思路是，每当遍历j时找到了第二个相加数，就直接把它从哈希表中erase()，这样后续即便nums[j+1]==nums[j]，由于哈希表中已经没有了符合三数和为0的第二个相加数，所以会find失败，也就不会加入结果向量res中了。这样便通过哈希表键唯一和erase()，分别完成了第二个和第三个相加数的去重。然而这种方法，会有一个特殊情况。如果遍历到的第二个数和第三个数的值正好相等，比如[-2,1,1,1,1]，i=0，首先j遍历到1时，哈希表存入了值1，当j=2，找到了符合条件的第二个数，将值三元组{-2,1,1}加入结果向量，并从哈希表中erase(1)。问题来了，当j=3时，会再次向哈希表中加入1，j=4时，判断找到第二个数并再次将值三元组加入res。因此，题解中加入了if(j>i+2 && nums[j]==nums[j-1] && nums[j-1]==nums[j-2]) continue;的条件语句，就是为了应对这种情况，避免将相同的值erase之后又重复加入哈希表，完成了对第二个相加数的完美去重。当然，也可以换种方式来简单理解：我们现在只需要返回两个相加数，因此如果数组nums中出现了三个以上的相同值，其实我们已经用不上了那么多了，因此第三个重复值开始便已经没有了意义，应该continue掉。

综上，改进后的哈希表解法，在确保索引去重（索引三元组单调递增）的基础上，直接用两层for循环（第一个数去重）+一个哈希表（后两个数去重），完成了值去重。时间复杂度为O(n2)，空间复杂度为O(n)。

此外，上述代码中还有一些小细节，比如第一层循环i时，如果nums[i]>0则直接break，因为后面两数都会比0大，三数之和不可能为0。节省了不必要的时间开销。这类细节还有一些，具体可参见代码注释。

其实这道题目使用哈希法并不十分合适，因为在去重的操作中有很多细节需要注意，在面试中很难直接写出没有bug的代码。

而且使用哈希法 在使用两层for循环的时候，能做的剪枝操作很有限，虽然时间复杂度是O(n^2)，也是可以在leetcode上通过，但是程序的执行时间依然比较长 。

接下来我来介绍另一个解法：双指针法，这道题目使用双指针法 要比哈希法高效一些，那么来讲解一下具体实现的思路。具体代码。

动画效果如下：

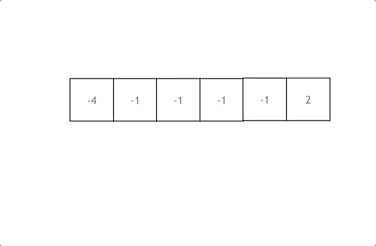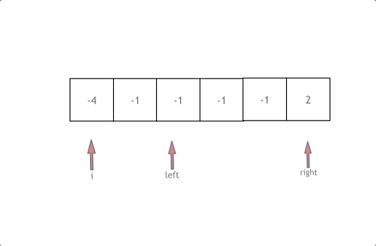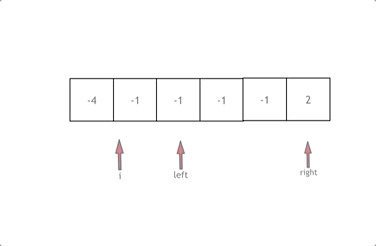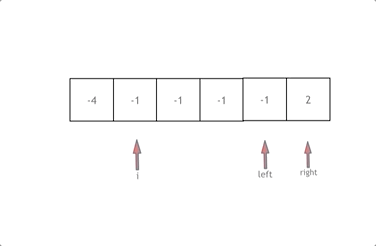
拿这个nums数组来举例，首先将数组排序，然后有一层for循环，i从下标0的地方开始，同时定一个下标left 定义在i+1的位置上，定义下标right 在数组结尾的位置上。

依然还是在数组中找到 abc 使得a + b +c =0，我们这里相当于 a = nums[i]，b = nums[left]，c = nums[right]。

接下来如何移动left 和right呢， 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了，因为数组是排序后了，所以right下标就应该向左移动，这样才能让三数之和小一些。

如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了，left 就向右移动，才能让三数之和大一些，直到left与right相遇为止。

如果nums[i] + nums[left] + nums[right] = 0说明三数之和正好，将值三元组保存到结果向量中，并让left向右移动，right向左移动。

如何进行去重操作呢？

索引去重：根据本题定义，三个相加数的索引一定满足i<left<right，可以保证遍历期间得到的满足条件的索引三元组单调递增。

值去重：第一个数：移动i时，如果i>0且nums[i]=nums[i-1]，则continue；这部分和哈希表同理；第二三个数：当三数和等于0时，在left/right移动前，先要进行去重，while(nums[left]==nums[left+1]) left++; while(nums[right]==nums[right-1]) right—;

时间复杂度：O(n2)，空间复杂度：O(logn)。排序的复杂度为O(logn)。比哈希表方法好了很多。

扩展：两数之和（Leetcode 1)能否使用双指针法呢？

两数之和 就不能使用双指针法，因为要求返回的是索引下标， 而双指针法一定要排序，一旦排序之后原数组的索引就被改变了。

如果两数之和 要求返回的是数值的话，就可以使用双指针法了。

---

11.Leetcode 18四数之和（题解）

难度：⭐️⭐️⭐️

本题算是上一道题目的扩展，用的方法也是大同小异，在外面再套一层for循环即可。本题的解法为两层for循环+双指针。有一些额外需要注意的细节：

• 在前面的几层循环时，i只用遍历到nums.size()-相加数个数，就可以了。
• nums.size()是size_type类型，也就是unsigned int，如果直接用i<nums.size()-3作为判断条件，当nums.size()-3表示负数时，会是很大的一个正数，因此这个表达式仍为true，违背了原本的预期。一个规避方法是，在代码开始添加if(nums.size()<=4)，return {}即可。
• 本题target是个变化值，而不像上一题恒为0。因此在剪枝时，我们不能直接用if(nums[i]>target) break; 来判断了，因为如果nums[i]和target都为负，多个负数相加和越来越小（而不像多个正数越加越大），因此其和仍有可能=target。解决方法是改成if(nums[i]>=0 && nums[i]>target) break;
• 多个数int数相加时，极端情况下可能会数据越界，因此需要将求和表达式的结果类型转为long int，以免不必要的错误
• 双指针遍历时，当和=target时，去重的判断条件为while(left<right && nums[left]==nums[left+1]) left++; 如果不写left<right可能会一直向右遍历直到越界。

具体实现代码。时间复杂度O(n3)，空间复杂度O(nlogn)，为快速排序所占用的递归栈空间。

关于剪枝部分，看了官方题解后，发现比我原来的方法更佳精妙，剪枝的范围也更佳精细，可以做到近乎完美剪枝，果断列出，供大家学习参考。优化后的代码​​​​​​​。

这里有个细节：>target的时候，直接break，因为后面的i只会让和更大; <target的时候，只是continue，因为后面的i还有可能让总和更大，有可能会达到target。

一样的道理，五数之和、六数之和等等都采用这种解法，继续在外面套一层for循环即可。

双指针法就是将原本暴力O(n^3)的解法，降为O(n^2)的解法，四数之和的双指针解法就是将原本暴力O(n^4)的解法，降为O(n^3)的解法。两数之和的双指针法将原本O(n2)的解法，降为O(nlogn)的解法（排序部分O(nlogn)，双指针遍历部分O(n)）

之前我们讲过哈希表的经典题目 Leetcode 454四数相加，相对于本题简单很多，因为本题是要求在一个集合中找出四个数相加等于target，同时值四元组不能重复。

而四数相加是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑值重复的问题，只需要保证索引不重复即可，所以相对于本题还是简单了不少！

---

总结

哈希表包含数组、set、map三种实现方式。

数组：当空间大小有限时（如只有小写字母），适合使用，相比setmap省去了哈希函数计算、维护哈希表的时间开销，效率更高。

set：只需判断元素是否重复出现时，适合使用。哈希表中只需要存储键。

map：除了需要判断元素是否重复出现，还需要保存一些额外信息（如两数之和的索引、四数相加的两数和出现次数）时，适合使用。

本文部分内容参考自：代码随想录

最后

以上就是温柔鸡为你收集整理的Leetcode 刷题笔记：哈希表篇的全部内容，希望文章能够帮你解决Leetcode 刷题笔记：哈希表篇所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。