1.题目

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

示例 1：

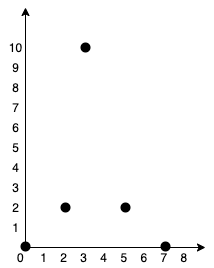
输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
解释：

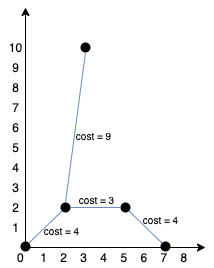
我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。

示例 2：
输入：points = [[3,12],[-2,5],[-4,1]]
输出：18

示例 3：
输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4

示例 4：
输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000

示例 5：
输入：points = [[0,0]]
输出：0

提示：
1 <= points.length <= 1000
-106 <= xi, yi <= 106
所有点 (xi, yi) 两两不同。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/min-cost-to-connect-all-points

2.思路

（1）Kruskal
思路参考Kruskal 最小生成树算法。

3.代码实现（Java）

//思路1————Kruskal
class Solution {
    public int minCostConnectPoints(int[][] points) {
        //一共有 n 个节点
        int n = points.length;
        /*
            生成所有边及权重，并用坐标点在 points 中的索引来表示坐标点
            int[]{坐标点i, 坐标点j, i 和 j 之间的曼哈顿距离}
        */
        List<int[]> edges = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int xi = points[i][0];
                int yi = points[i][1];
                int xj = points[j][0];
                int yj = points[j][1];
                edges.add(new int[]{i, j, Math.abs(xi - xj) + Math.abs(yi - yj)});
            }
        }
        //将边按照权重进行升序排序
        Collections.sort(edges, (a, b) -> {
            //返回值为正，则交换 a 和 b
            return a[2] - b[2];
        });
        //Kruskal 算法
        int res = 0;
        UnionFind uf = new UnionFind(n);
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            int weight = edge[2];
            //选中的边会产生环，则不能将其加入最小生成树中
            if (uf.isConnected(u, v)) {
                continue;
            }
            //如果选中的边不会产生环，则它属于最小生成树
            res += weight;
            //将节点 u 和 v 进行连通
            uf.union(u, v);
        }
        return res;
    }
    
    //并查集
    //并查集
    class UnionFind {
        //记录连通分量(树)的个数
        private int count;
        //节点 x 的根节点是 root[x]
        private int[] root;
    
        //构造函数
        public UnionFind(int n) {
            //初始时每个节点都是一个连通分量
            this.count = n;
            root = new int[n];
            //初始时每个节点的根节点都是其自己，即每棵树中只有一个节点
            for (int i = 0; i < n; i++) {
                root[i] = i;
            }
        }
    
        //将 p 和 q 连通
        public void union(int p, int q) {
            int rootP = find(p);
            int rootQ = find(q);
            if (rootP == rootQ) {
                // p 和 q 的根节点相同，它们本就是连通的，直接返回即可
                return;
            } else {
                root[rootQ] = rootP;
                // 两个连通分量合并成一个连通分量
                count--;
            }
        }
    
        //判断 p 和 q 是否互相连通，即判断 p 和 q 是否在同一颗树中
        public boolean isConnected(int p, int q) {
            int rootP = find(p);
            int rootQ = find(q);
            //如果 p 和 q 的根节点相同，则说明它们在同一颗树中，即它们是连通的
            return rootP == rootQ;
        }
    
        //查找节点 x 的根节点
        public int find(int x) {
            if (root[x] != x) {
                root[x] = find(root[x]);
            }
            return root[x];
        }
    
        //返回连通分量(树)的个数
        public int getCount() {
            return count;
        }
    }
}

最后

以上就是超帅可乐为你收集整理的LeetCode_Kruskal_中等_1584. 连接所有点的最小费用1.题目2.思路3.代码实现（Java）的全部内容，希望文章能够帮你解决LeetCode_Kruskal_中等_1584. 连接所有点的最小费用1.题目2.思路3.代码实现（Java）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。