Project Euler 41-45题

74 阅读 0 评论 49 点赞

我是靠谱客的博主义气牛排，最近开发中收集的这篇文章主要介绍Project Euler 41-45题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

第41题

这里写图片描述
题目来源ProjectEuler
该题求由1-n的数字的全排列构成的数中，最大的素数。
显然n小于等于九。而若n=9，则 $sum_{i=1}^9i=45$ ，是9的倍数，所以 $n leq 8$ 。
我们利用prev_permutation()函数，求一个全排列的上一个全排列，而运行 $len!$ 次后将会回到初始排列。我们枚举全排列的长度，由长至短依次检验，一旦成功则输出并结束程序。

#include<bits/stdc++.h>
using namespace std;

bool check(long long x){
    for (long long i=2;i*i<=x;i++){
        if (x%i==0) return false;
    }
    return true;
}

int main(){
    int f[10]={1,};
    for (int i=1;i<=9;i++)  f[i]=f[i-1]*i;  
    char x[]={'1','2','3','4','5','6','7','8',''};
    int ans=0;
    for (int maxx=8;maxx>=1&&!ans;maxx--){
        for (int i=1;i<=f[maxx]&&!ans;i++){
            prev_permutation(x,x+maxx);
            long long tmp=0;
            for (int j=0;j<maxx;j++){
                tmp=tmp*10+x[j]-'0';
            }
            if (check(tmp)) ans=tmp;
        }
    }
    cout<<ans<<endl;
    return 0;
}

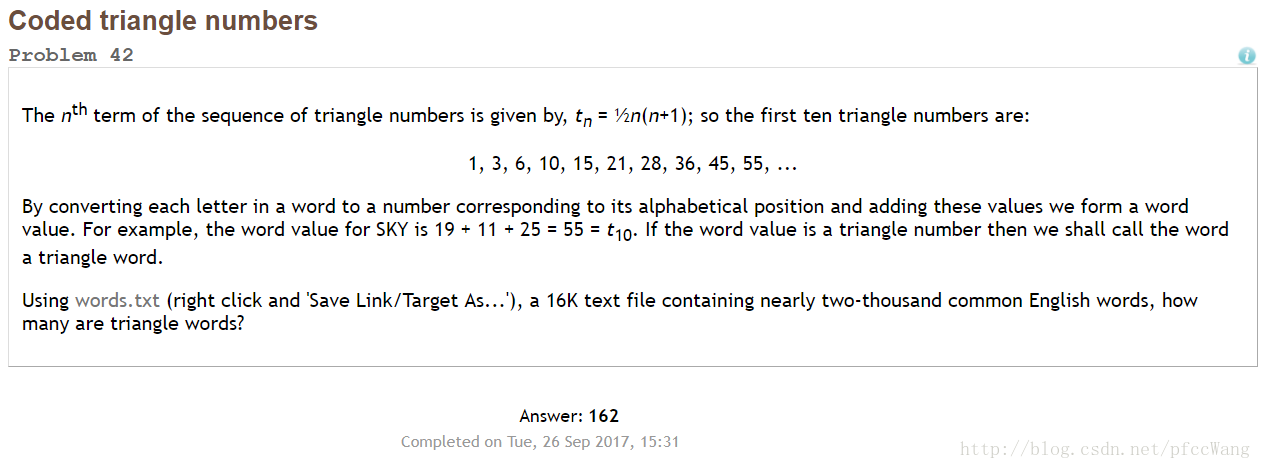
第42题

这里写图片描述
题目来源ProjectEuler
题中words.txt的地址
该题求给定的文件中，单词在26字母表中位置之和（初始位置pos[A]=1）是否为triangle number。

先算出一百个triangle number，然后读入单词，若满足条件则ans++

#include<bits/stdc++.h>
using namespace std;

int main(){
    int num[10000];
    for (int i=1;i<=100;i++)    num[i*(i+1)/2]=1;
    freopen("../in.in","r",stdin);
    char tmp[100000];
    int ans=0;
    scanf("%s",&tmp);
    for (int i=1,sum=0;tmp[i];i+=3,sum=0){
        for (;tmp[i]!=34;i++)   sum+=tmp[i]-'A'+1;
        if(num[sum])    ans++;  
    }
    cout<<ans<<endl;
    return 0;
}

第43题

这里写图片描述
题目来源ProjectEuler

求0-9构成的所有全排列构成的数中，满足如题7个等式的所有数的和。利用next_permutation()模拟一遍即可。

#include<bits/stdc++.h>
using namespace std;

int prime[10]={0,2,3,5,7,11,13,17,19,};

int main(){
    int num[11]={1,0,2,3,4,5,6,7,8,9,};
    int maxn=3628800-362880;
    long long ans=0;
    for (int tmp=0,boolean=1,i=1;i<=maxn;boolean=1,tmp=0,i++){
        for (int tmp=0,j=1;j<8&&boolean;tmp=0,j++){
            for (int k=j;k<=j+2;k++){
                tmp=tmp*10+num[k];
            }
            if(tmp%prime[j]!=0) {boolean=0;break;}
        }
        if (boolean){
            long long tmp=0;
            for (int j=0;j<10;j++){
                tmp=tmp*10+num[j];
            }
            cout<<tmp<<endl;
            ans+=tmp;
        }
        next_permutation(num,num+10);
    }
    cout<<ans<<endl;
    return 0;
}

第44题

这里写图片描述
题目来源ProjectEuler

这个题定义了一个数列的通项公式 $P_n=n(3n-1)/2$
求数列中的 $P_A,P_B,P_C,P_D$ ，满足 $P_A=P_B-P_C且P_B+P_C=PD$
这个题我确实没有很好地实现方法，没有办法证明应当找前几位，只是试探性地在前3000项中枚举 $P_B,P_C$ ，然后判断 $P_A,P_D$ 是否在数列中。

#include<bits/stdc++.h>
using namespace std;

int num[10001];
int occur[40000000];

int main(){
    for (int i=1;i<=6000;i++)   num[i]=i*(3*i-1)/2,occur[num[i]]=1;
    int ans=1<<30;
    for (int i=1;i<=3000;i++){
        for (int j=1;j<i;j++){
            if(occur[num[i]+num[j]]&&occur[num[i]-num[j]]){
                ans=min(ans,num[i]-num[j]);
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}

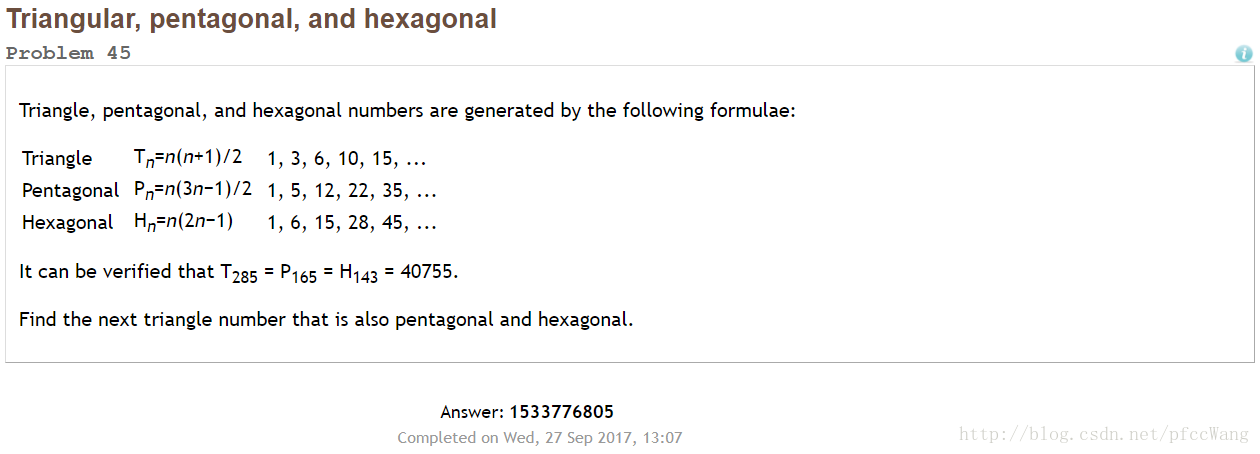
第45题

这里写图片描述
题目来源ProjectEuler

题中给出了三个数列的通项公式，已知 $T_{285}=P_{165}=H_{143}=40755$ ，求下一个出现在三个数列中的数的值。
同样也只能推测这个数不会太大，然后枚举 $H_n$ ，检查这一项是否在前两个数列中。复杂度姑且记为 $O(nlog n)$

#include<bits/stdc++.h>
using namespace std;

bool check1(long long l,long long r,long long aim){
    if (l==r)   return l*(l+1)/2==aim;
    long long mid=l+r;mid>>=1;
    if (mid*(mid+1)/2>=aim) return check1(l,mid,aim);
    else                    return check1(mid+1,r,aim);
}

bool check2(long long l,long long r,long long aim){
    if (l==r)   return l*(3*l-1)/2==aim;
    long long mid=l+r;mid>>=1;
    if (mid*(3*mid-1)/2>=aim)   return check2(l,mid,aim);
    else                        return check2(mid+1,r,aim);
}

int main(){
    for (long long i=144;;i++){
        if (check1(1,i*(2*i-1),i*(2*i-1))&&check2(1,i*(2*i-1),i*(2*i-1))){
            cout<<i*(2*i-1)<<endl;
            break;
        }
    }
    return 0;
}