循环码编码与译码（MATLAB实现）

循环码的定义

循环码是一类满足循环特性的线性分组码，线性分组码对码的选取做了线性约束，而循环码是在线性约束的基础上增加了满足循环性的约束条件，是线性分组码的子类。下面以二元循环码进行说明。
由于 (n,k,d) 线性分组码是 n 维线性空间 V_n 的一个线性子空间 V_n,k ，如果对于 n 重子空间 V_n,k，任何一个 V=(V_n-1,V_n-2,…,V₀)∈V_n,k，恒有 V₁=(V_n-2,V_n-3,…,V₀,V_n)∈V_n,k，则称 V_n,k 为循环子空间或循环码。
实际上，对于一个 (n,k,d) 线性分组码，若其任一码字 C=(c_n-1,c_n-2,…,c₀) 循环移位后得到的码字 C⁽ⁱ⁾=(c_i+1,c_i+2,…,c_n,c₁,c₂,…,c_i) 均为该线性分组码的码字，则称该 (n,k,d) 线性分组码为循环码。
循环码具有规则的代数结构，且是子封闭的，因此用多项式描述更为方便。长度为 n 的循环码可以用一个 n-1 次多项式来表示，称为码多项式，表示为：

左移 i 位后的码多项式为：

码多项式和循环移位后的多项式之间的关系为：

即：

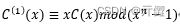
依此类推，可以得到：

以上便是循环码的定义。

循环码的性质

(n,k) 循环码 C 有如下性质：
一、GF(q) 上的 (n,k) 循环码中，存在唯一的一个 n-k 次首一多项式：

每一个码多项式 C(x) 都是 g(x) 的倍式，即循环码的码多项式 C(x) 中次数最低且其常数项为 1 的码多项式有且只有 1 个，为码的生成多项式，记作 g(x)。循环码 C 中的每个码多项式 C(x) 都可以唯一表示成 C(x)=m(x)g(x)。
二、 g(x)，xg(x)，x²g(x)，……，x^k-1g(x) 都是生成多项式，他们的线性组合亦然。
三、GF(q) 上的 (n,k) 循环码的生成多项式 g(x) 一定是 (xⁿ-1) 的因子，反之若 g(x) 的次数为 n-k 且 g(x)|(xⁿ-1)，则该 g(x) 一定生成一个 (n,k) 循环码。
四、循环码的生成矩阵 G 和校验矩阵 H 的正交特性可以用多项式形式表示为 g(x)h(x)=xⁿ-1。因此 h(x) 也是 xⁿ-1 的因子。
五、生成矩阵 G 中的每一行都是另一行经过循环移位之后的结果。

循环码的生成矩阵

根据 (n,k) 循环码的性质 g(x)h(x)=xⁿ-1，若 g(x) 的次数为 n-k 次，以 g(x) 作为生成多项式组成的 (n,k) 循环码的 k 个码多项式 g(x)，xg(x)，x²g(x)，……，x^k-1g(x) 一定是线性无关的，根据线性分组码的定义，这些码多项式可以构成循环码的生成矩阵多项式 G(x)：

从而，(n,k) 循环码的生成矩阵 G 为：

从上式可见，生成矩阵的每一行都是上一行右移一位的结果。

循环码的校验矩阵

定义 (n,k) 循环码的校验多项式为：

根据 g(x)h(x)=xⁿ-1，得到系数方程：

通过解方程组，可以得到 (n,k) 循环码的校验矩阵 H 为：

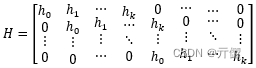
可以验证：

循环码的生成

由于循环码的每个码多项式 C(x) 都是生成多项式 g(x) 的倍式，所以 g(x) 的根是所有码多项式 C(x) 的根，因此可以根据生成多项式的根来定义和生成循环码。
对于 GF(2) 上 (n,k) 循环码的生成多项式 g(x)，一定可以在某个 GF(2) 的扩域上完全分解，也即：

其中，α_i 为多项式 g(x) 的根，且 α_i∈GF(2^m) 。对于无重根的情况，如前所述， (n,k) 循环码的每一个码多项式 C(x) 也以生成多项式 g(x) 的根。因此对于码多项式有：

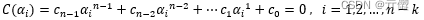
写成矩阵形式，有：

从而得到 (n,k) 循环码的校验矩阵 H：

根据校验矩阵 H 可以得到 (n,k) 循环码的生成多项式 G。
若 α_i 的最小多项式为 m_i(x),i=1,2,…,n-k，则仅只有生成多项式 g(x) 和码多项式 C(x) 均能被这些最小多项式整除时，g(x) 和 C(x) 才能以 α_i,i=1,2,…,n-k 为根。由于生成多项式 g(x) 是码多项式中唯一的次数最低的首一多项式，因此有：

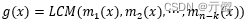
其中，LCM() 为最小公倍数。因此，求 (n,k) 循环码的生成多项式的关键是找出每个根的最小多项式。
由于多项式 xⁿ-1 能够整除生成多项式 g(x)，因此 g(x) 的根也是多项式 xⁿ-1 的根，所有每个根 α_i 的级 e_i,i=1,2,…,n-k 必须能够被 n 整除，从而可知循环码的码长为：

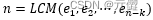
例：求 GF(2³) 上以 α，α²，α⁴ 为根的循环码。最小多项式为 m₁(x)=x³+x+1，以此作为循环码的生成多项式 g(x)，码长 n 为 α 的级数 2³-1=7，生成多项式的次数为 n-k=3，因此生成（7，4）循环码。

循环码的译码

循环码作为线性分组码的子类，自然可以用伴随式进行译码。另外，利用循环码的循环码特性，可以实现更为简单有效的捕错译码。

伴随式译码

循环码的伴随式译码与线性分组码的伴随式译码思想相同，都包括根据接收码字 R 和校验矩阵 H 计算伴随式 S、根据伴随式 S 和编码规则估计错误图样 E 以及根据接收码字 R 和估计的错误图样 E 得到译码码字 C 等步骤。具体可见链接：(https://blog.csdn.net/weixin_45115771/article/details/125559103?spm=1001.2014.3001.5501)

捕错译码

捕错译码的基本思想是通过将接收码字中的错误集中并判断伴随式的重量实现译码，针对系统码的译码使用。
对于 (n,k) 系统循环码（码字中的前 k 个码元为信息元），假设信息多项式为 m(x)，发送码字多项式为 ：

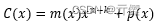
其中，p(x) 为校验元对应的多项式，信道错误图样为：

其中，信息部分的错误图样如下：

校验部分的错误图样如下：

接收码多项式为 R(x)，则伴随式多项式为：

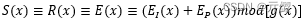
如果错误图样多项式 E(x) 的次数小于等于 n-k-1，则所有错误都集中在校验元上，此时

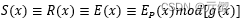
而校验部分的错误图样的次数低于生成多项式的次数 n-k，因此伴随式 S 就是错误图样 E。从而纠错过程就简化为：C^=R+S。
实际上，任一 (n,k,d) 线性分组码的最大最小距离等于 n-k+1。循环码作为线性分组码的一类，有条件限制且纠错能力 t<d。如果码字中出现的所有小于等于 t 个错误出现在连续的 n-k 位，则要求循环码的参数满足信息组长度 k<n/t 或纠错能力 t<n/t。
根据循环码的性质，对于能够纠正 t 个错误的 (n,k) 循环码，经过 i 次循环移位后的接收码多项式 R_i(x) 对应的伴随式 S_i 的重量小于等于 t 的充要条件是所有小于等于 t 个错误都集中再来移位后的码字的后 n-k 位。首先，如果错误已经集中在码字的低 n-k 位，则有：

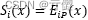
由于该 (n,k) 循环码能够纠正小于等于 t 个错误，如果错误图样是可纠正的，则必有：

从而该错误图样经过 i 次循环移位后的错误图样重量保持不变。另一方面，如果错误图样的重量小于等于 t ，而错误没有集中，则经过 i 次循环移位后的错误图样的次数大于生成多项式的次数，从而有：

由于 C_i(x) 是生成多项式的倍式，因此必是该 (n,k) 循环码的码字，因此其重量要大于等于码的最小距离，另外根据 t=floor((d-1)/2) 可得到：

也即，如果错误没有集中在码字的底 n-k 位，则伴随式的重量必大于 t，与假设条件不符。
根据循环码的伴随式多项式与接收码多项式及循环移位结果之间的对应关系，将接收码多项式 R(x) 及其相应的伴随多项式 S₀(x) 循环 i 次后，如果检测到以为后的伴随式的重量小于等于 t，则认为此时错误已经集中在码字的后 n-k 位其伴随式 S_i=(xⁱS₀(x))mod[g(x)] 就是 xⁱR(x)mod[xⁿ-1] 的伴随式，这样就可以直接在 R 上减去 S 实现纠错，然后利用循环码的循环移位特性，再循环 n-i 次恢复码元原来的顺序，完成纠错译码。

MATLAB仿真实现

1、在matlab中，用一条语句即可实现循环码的编码，如下：

code = encode(msg,n,k,'cyclic',g);

其中，msg待编码信息组， 是n 是码长，k 是信息组长度，g 是生成多项式的系数。

2、循环码的译码（捕错译码）matlab仿真实现如下：

g_len = length(g); % g为(n,k)循环码的生成多项式
shift_reg = zeros(1,g_len-1); % 初始化n+(n-k)=n级缓存器
flag = 1;

% 将接收码字移入n级缓存和伴随式计算电路
for i=1:n
    for j=1:n-1
        cache_mem(n-j+1) = cache_mem(n-j);
    end
    cache_mem(1) = rec(i);
    % 伴随式计算电路根据输入和移位寄存器的值计算伴随式
    temp = shift_reg(g_len-1);
    for j=1:g_len-2
        shift_reg(g_len-j) = rem(shift_reg(g_len--j-1)+temp*g(g_len-j),2);
    end
    shift_reg(1) = rem(rec(i)+temp*g(1),2);
end

% 判断伴随式的重量是否小于等于纠错能力 t
if sum(shift_reg)<=t
    cache_mem = [rem(cache_mem(1:n-k)+shift_reg,2) cache_mem(n-k+1:n)];
    for i=1:n
        code(i) = cache_mem(n-i+1);
    end
else
    i = 1;
    while i<n & flag
        temp1 = cache_mem(n);
        for j=1:n-1
            cache_mem(n-j+1) = cache_mem(n-j);
        end
        cache_mem(1) = temp1;
        temp = shift_reg(g_len-1);
        for j=1:g_len-2
            shift_reg(g_len-j) = rem(shift_reg(g_len-1-j) + temp*g(g_len-j),2);
        end
        shift_reg(1) = temp*g(1);

        if sum(shift_reg)<=t
            cache_mem = [rem(cache_mem(1:n-k)+shift_reg,2) cache_mem(n-k+1:n)];
            flag = 0;
        end
        i = i+1;
    end
    i = i-1;
    if flag
        code = zeros(1,n);
    else
        for j=1:n-i
            temp1 = cache_mem(n);
            for j=1:n-1
                cache_mem(n-j+1) = cache_mem(n-j);
            end
            cache_mem(1) = temp1;
        end

        for i=1:n
            code(i) = cache_mem(n-i+1);
        end
    end
end

需要注意的是，在使用捕错译码算法的时候，其对应的应是系统循环码。

最后

以上就是谦让心情为你收集整理的循环码编码与译码（MATLAB实现）的全部内容，希望文章能够帮你解决循环码编码与译码（MATLAB实现）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。