2D-2D对极几何

今天跟着视觉SLAM十四讲 重新推导了一下2D-2D的对极几何公式,对坐标变化公式$P_{c2}=R\times P_{c1}+t$又有了新的认识
先放上参考链接:https://www.cnblogs.com/houkai/p/6661607.html

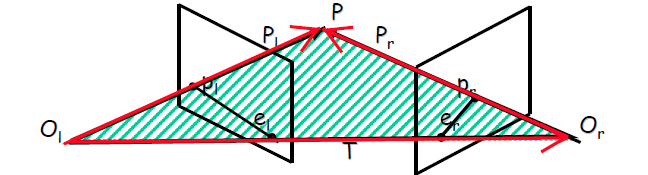
这里面到的这么一个关系:$P_{c2}=R(P_{c1}-T)$($T$是两个相机光心之间的平移,注意此时是在$P_{c1}$的坐标系下的),感觉很难理解,细想之后,搞明白了相机在做变换时候旋转和平移的先后顺序。
我们平时用的公式$P_{c2}=P_{c1}\ast R+t$,实际上是先做了旋转,然后再在旋转后的坐标系下平移$t$,这时的小$t$其实对我们而言并不直观,因为我们更倾向于它在$P_{c1}$坐标系下的表示(我们一般会直接把$P_{c1}$坐标系看作世界坐标系),而$T$则直观很多,它直接表示了$P_{c1}$到$P_{c2}$在世界坐标系($P_{c1}$坐标系)下的位移。再由公式来看：

$P_{c2}=R（P_{c1}-T）=R\times P_{c1}-R\times T=R\times P_{c1}+t$
得到:$t=-R\times T$

这就更直观的看到，其实他们之间的关系就是一个旋转的关系，至于负号，R代表的是光心之间的平移，反映到点的坐标变换时，应该加个负号（例如坐标系整体右移5个单位，坐标系中的点的横坐标都会减5）

总之，我们平时用的$t$，它表示的平移并不是我们直观看到的平移，而是相对与旋转之后的坐标系的平移。

搞清楚了这个，接下来就是对极几何的公式推导了，我直接手写吧：
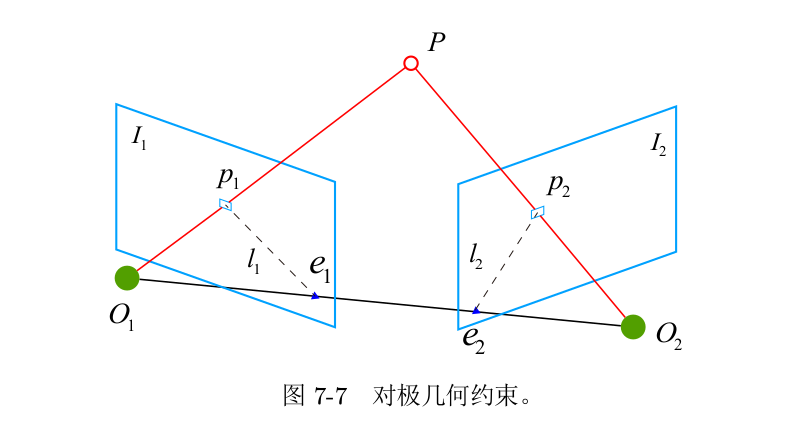
对极几何的约束:

$p_2^T{K}^{-T}t$^$R{K}^{-1}{p}_1=0$

本质矩阵: $E=t$^$R$
基础矩阵: $F=K^{-T}E{K}_{-1}$
则对极几何约束为: $p_2^{T}F{p}_1=0$
根据匹配点的像素,求出E或F,然后求出R和t。

最后

以上就是会撒娇菠萝为你收集整理的2D-2D对极几何的全部内容，希望文章能够帮你解决2D-2D对极几何所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。