2.有限的马尔可夫决策过程

环境：智能体之外所以与之相互作用的事物。
智能体：进行学习及实时决策的机器。

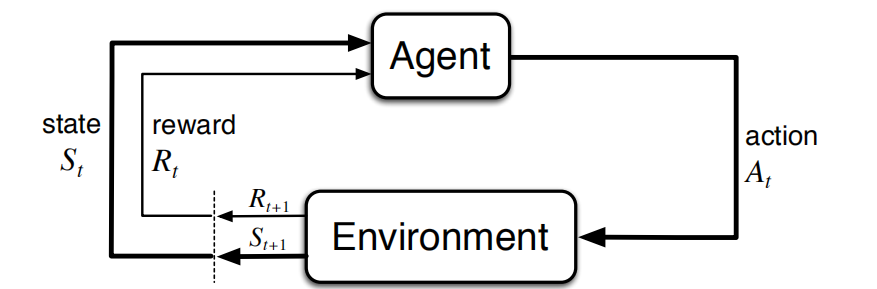
在有限的MDP中，状态，动作和收益的集合（S,A,R）都只有有限个元素。

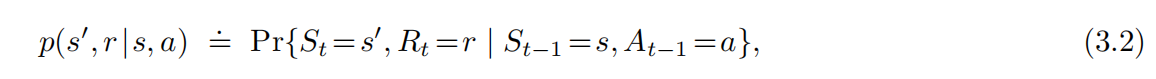
目标和收益

收益：在强化学习中，智能体的目标被形式化表征为一种特殊信号，收益通过环境传递给智能体。收益都是单一的标量数值。
收益假设：我们所有的“目标”或“目的”都可以归结为：最大化智能体接收到的标量信号（称之为收益）累积和的概率期望值

回报和分幕（Episodes）

在最简单的情况下，回报就是收益的总和：

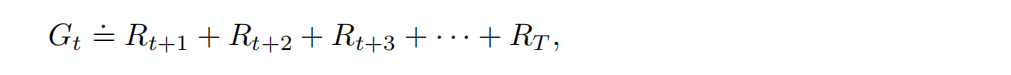
T为最终时刻。
最大期望折扣回报：

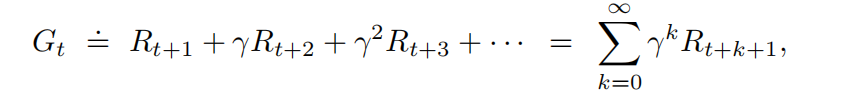
邻接时刻的回报：

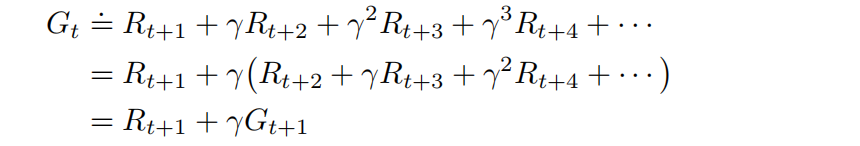
回报：当收益为为常数+1时。

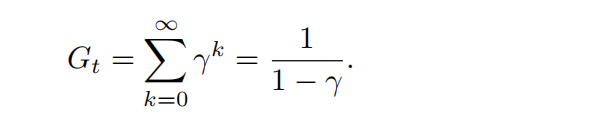
策略和价值函数

价值函数：是状态（动作-状态二元组）的函数，用来评估当前智能体在给定状态下有多好。
“有多好”：是用未来预期的收益来定义的，更确切地说是回报的期望值。
价值函数与特定行为方式相关的，我们称之为策略。
策略：严格来说，是从状态到每个动作的选择概率之间的映射。

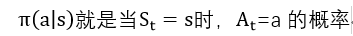
中间的 “|”，只是提醒我们它为每个s∈S都定义了一个 a∈A上的概率分布。而 p的“|”表示条件概率，函数p为每个s和a的选择都指定了一个概率分布。


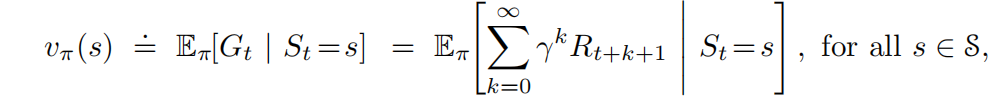
E[·]表示给定策略π时的一个随机变量值，t可以是任意时刻。
类似地，我们把策略π下在状态s下采取动作a的价值记为q（s,a）,根据策略π，从状态s开始，采取动作a之后，所有可能的决策序列的期望回报：

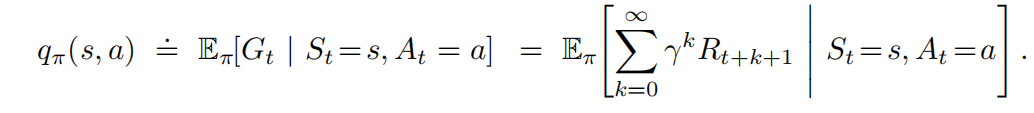
回溯图：

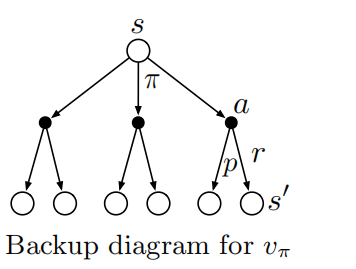
贝尔曼方程

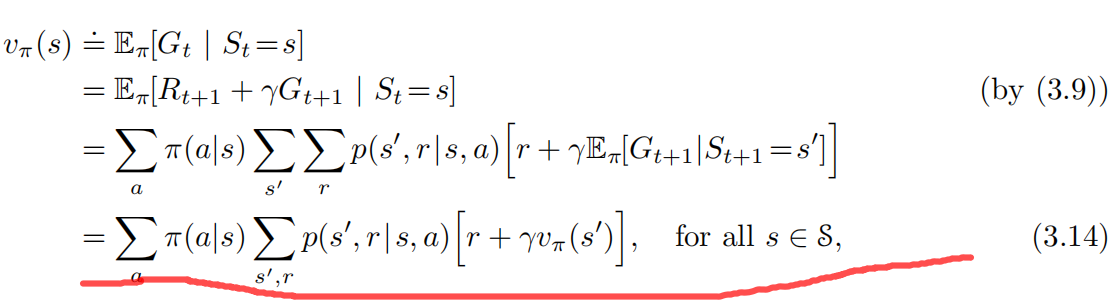
最优策略和最优价值函数

最优策略不止一个。
最优状态价值函数：

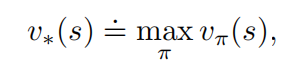
最优动作价值函数：
、
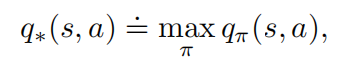用v来表示q：

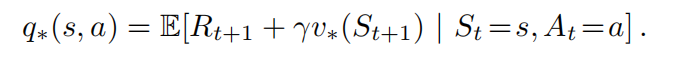
v的贝尔曼最优方程：阐述了一个事实，最优策略下各个状态的价值一定等于这个状态下最优动作的期望回报。

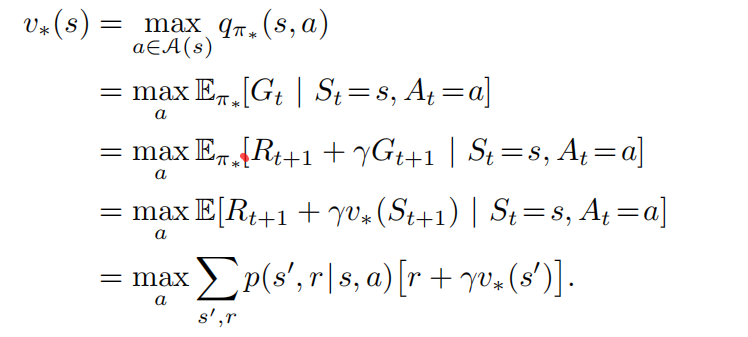
最后两个等式是贝尔曼最优方程的两种形式。
q的贝尔曼最优方程如下：


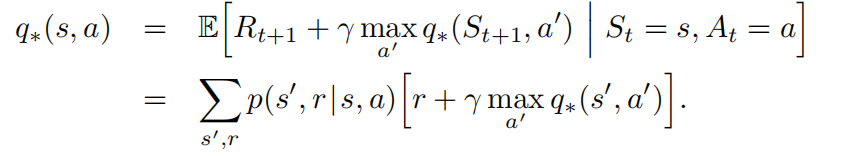
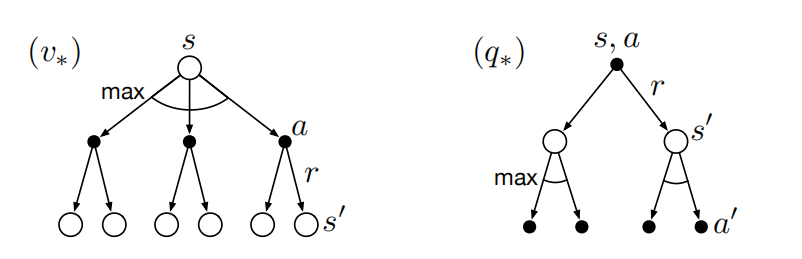
给定策略下取其最大值，max。
一但有了v*，确定最优策略就比较容易。对于v来说没任何贪心策略都是最优的。
定义v的意义在于，我们可以将最优的长期（全局）回报期望值转化为每个状态对应的一个当前局部量的计算。

最优性和近似算法

小结

在强化学习中，智能体及其环境在一连串离散时刻上进行交互。这两者之间的接口定义了一个特殊的任务：动作由智能体选择，状态是做出选择的基础，收益是评估选择的基础。智能体内部的所有事物对于智能体来说是完全可知、完全可控的。策略是智能体选择动作的随机规则，它是状态的一个函数。智能体的目标就是随着时间的推移来最大化总的收益。

最后

以上就是着急薯片为你收集整理的2.有限的马尔可夫决策过程的全部内容，希望文章能够帮你解决2.有限的马尔可夫决策过程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。