一.舍罕王赏麦
【问题描述】
据说印度的舍罕王打算重赏一个宰相,问他有何要求?
这位宰相说:“陛下,请您在这张棋盘的第一个格内赏给我一粒麦子,在第二个格内赏给我两粒麦子,
在第三个格内赏给我四粒麦子,照这样每一格内都比前一个格多一倍,把这棋盘的64个给都放满就行啦。”
舍罕王听后,认为这区区赏金微不足道,于是满口答应道:“爱卿,你所要求的并不多啊,你当然如愿以偿。”
请问:共需要赏赐给这位宰相多少粒麦子?
【设计思路】
通过循环计算当前格子的麦子数及当前所有格子的麦子数之和。
def shehanwang(n):
"""计算舍罕王赏给宰相的麦子数"""
t = 1 # 初始化当前格子的麦子数
s = 1 # 初始化当前所有格子的麦子数之和
# 通过循环计算当前格子的麦子数及当前所有格子的麦子数之和
for _ in range(2, n + 1):
t *= 2 # 计算当前格子的麦子数
s += t # 计算当前所有格子的麦子数之和
return s
print('舍罕王赏赐给宰相的麦子数:', shehanwang(64))
舍罕王赏赐给宰相的麦子数: 18446744073709551615
# 使用列表生成式,一行语句就能搞定
print('舍罕王赏赐给宰相的麦子数:', sum([2 ** i for i in range(64)]))
舍罕王赏赐给宰相的麦子数: 18446744073709551615
二.不重复的三位数
统计0-9这10个数字可以组成多少个不重复的三位数?
设计思路:
根据排列组合的数学知识可知:0-9这10个数字可以组成不重复的三位数的个数为:9 * 9 * 8 = 648
设三位数的百位、十位和个位分别为a、b和c,其取值范围分别为[1,9]、[0,9]和[0,9]
通过三重循环穷举a、b和c的值,在穷举的过程中,只要三者两两不相等,就找到了一个符合条件的解。
counter = 0
# 设三位数的百位、十位和个位分别为a、b和c,其取值范围分别为[1,9]、[0,9]和[0,9]
# 通过三重循环穷举a、b和c的值
for a in range(1, 10):
for b in range(10):
for c in range(10):
# 在穷举的过程中,只要三者两两不相等,就找到了一个符合条件的解
if a != b and b != c and c != a:
counter += 1
print(counter)
648
counter = 0
for a in range(1,10):
for b in range(10):
if a == b:
continue
for c in range(10):
if b != c and c != a:
counter += 1
print(counter)
648
三.角谷猜想
【问题描述】
日本的角谷提出了一个问题,猜想的内容是:对于任意的自然数,反复进行如下运算:
1.若为奇数,则乘以3后加1;
2.若为偶数,则除以2.
总可以得到运算结果1
到目前为止,既不能证明角谷猜想是正确的,也不能举出反例说明角谷猜想是错误的。
对于任意给定的自然数,验证角谷猜想
【设计思路】
通过循环反复进行角谷猜想中的两种运算,当运算结果为1时则退出循环。
def jiaogu(n):
"""对于任意的自然数,验证角谷猜想"""
nc = n
# 通过循环反复进行角谷猜想中的两种运算,当运算结果为1时则退出循环。
while nc != 1:
nc = nc * 3 + 1 if nc % 2 else nc / 2
print('%d符合角谷猜想' % n)
jiaogu(18)
jiaogu(27)
18符合角谷猜想
27符合角谷猜想
四.鸡兔同笼
【问题描述】
在同一个笼子里有若干只鸡和兔,从上面数共有h个头,从下面数共有f只脚。
求笼子里鸡和兔的只数
【设计思路】
设鸡和兔的只数分别为x和y,根据题意可得知如下方程组:
x + y = h (1)
2x + 4y = f (2)
由方程(1)可知,x的取值范围是[1,h - 1],且y = h - x.
通过循环穷举x,在穷举的过程中,只要x满足方程(2),则得到了符合条件的解。
def chicken_rabbit(h, f):
for x in range(1, h):
y = h - x
if 2 * x + 4 * y == f:
print('鸡的只数:%d,兔的只数:%d' %(x,y))
return
chicken_rabbit(35,94)
鸡的只数:23,兔的只数:12
五.百钱买百鸡
【问题描述】:
用100文钱买100只鸡,其中公鸡5文钱1只,母鸡3文钱1只,小鸡1文钱3只。
求各买了几只公鸡、母鸡和小鸡。
【设计思路】
设计思路一:
设计公鸡、母鸡和小鸡的只数分别为x、y和z,根据问题描述可以得到如下方程组:
x + y + z = 100
5x + 3y + z/3 = 100
如果100文钱全买公鸡,最多可买20只,x取值范围:[0,20]
如果100文钱全买母鸡,最多可买33只,y取值范围:[0,33]
如果100文钱全买小鸡,最多可买300只,又因为总共买了100只鸡,所以z的取值范围:[0,100],且z能被3整除
通过三重循环穷举x,y和z的值。
在穷举的过程中,只要x,y和z满足上面的方程组,则得到一组符合条件的解。
for x in range(21):
for y in range(34):
for z in range(0,100,3):
if x + y + z == 100 and 5 * x + 3 * y + z / 3 == 100:
print('公鸡的只数:%d,公鸡的只数:%d,公鸡的只数:%d' % (x, y, z))
公鸡的只数:0,公鸡的只数:25,公鸡的只数:75
公鸡的只数:4,公鸡的只数:18,公鸡的只数:78
公鸡的只数:8,公鸡的只数:11,公鸡的只数:81
公鸡的只数:12,公鸡的只数:4,公鸡的只数:84
设计思路二:(二重循环就行了)
通过二重循环穷举x和y的值
在穷举的过程中,求出z = 100 - x - y,
只要z满足:z >= 0 且 z能被3整除 且5x + 3y + z/3 =100,
则得到一组符合条件的解
for x in range(21):
for y in range(34):
z = 100 - x - y
if z >= 0 and z % 3 == 0 and 5 * x + 3 * y + z / 3 == 100:
print('公鸡的只数:{},公鸡的只数:{},公鸡的只数:{}'.format(x, y, z))
公鸡的只数:0,公鸡的只数:25,公鸡的只数:75
公鸡的只数:4,公鸡的只数:18,公鸡的只数:78
公鸡的只数:8,公鸡的只数:11,公鸡的只数:81
公鸡的只数:12,公鸡的只数:4,公鸡的只数:84
六.谁家孩子跑得最慢
【问题描述】
张家、王家和李家各有三个孩子
一天,三家的九个孩子在一起比赛跑步,规定:
跑第一名得9分,跑第二名得8分,跑第三名得7分,…跑第九名得1分。
比赛结果如下:
1.各家三个孩子的总分相同。
2.第一名是李家的孩子,第二名是王家的孩子。
3.所有孩子的名次没有并列的。
4.各家三个孩子的名次都没有相连的。
求最后一名是谁家的孩子
【设计思路】
由1可知:
各家三个孩子的总分都是:(1+2+3+4+5+6+7+8+9)/3=15
由2可知:
因为第一名是李家的孩子,所以可设李家孩子的分数分别为:9、x、15-(9-x),即:9、x、6-x
其中,x的取值范围:[1,5]
因为第二名是王家的孩子,所以可设王家孩子的分数分别为:8、y、15-(8-y),即:9、y、7-y
其中,y的取值范围:[1,6]
由3和4可知:
x - (6 - x) > 1, y - (7 - y) > 1
通过循环穷举李家三个孩子的分数和王家三个孩子的分数,
在穷举的过程中,定义一个列表存放所有名次对应的分数。
每穷举一次李家三个孩子的分数,就把李家三个孩子的分数从列表中删除;
每穷举一次王家三个孩子的分数,就把王家三个孩子的分数从列表中删除;
列表中剩余的元素即为张家三个孩子的分数,从大到小分别为zhang[2],zhang[1],zhang[0]
因为张家三个孩子的名次也没有相连的,
所以zhang[2] - zhang[1] > 1,且zhang[1] - zhang[0] > 1
def slowest_child():
for li in [[9, x, 6 - x] for x in range(1, 6) if x - (6 - x) > 1]:
scores = list(range(1, 10))
for score in li:
scores.remove(score)
for wang in [[8, y, 7 - y] for y in scores if 7 - y in scores and y - (7 - y) > 1]:
for score in wang:
scores.remove(score)
zhang = scores
if zhang[2] - zhang[1] > 1 and zhang[1] - zhang[0] > 1:
print('李家三个孩子的分数:', li)
print('王家三个孩子的分数:', wang)
print('张家三个孩子的分数:', zhang)
slowest_child()
李家三个孩子的分数: [9, 4, 2]
王家三个孩子的分数: [8, 6, 1]
张家三个孩子的分数: [3, 5, 7]
七.杨辉三角
from IPython.display import Image
Image(filename = 'F:/Jupyter/Python/lizi.jpg', width=400, height=200)

【设计思路】
杨辉三角的特点:
1.第i行有i个数
2.每行的第一个数和最后一个数都是1
3.每行除了第一个数和最后一个数,其余各数都是其两肩上的数之和
如果将所有的数存在一个二维列表L中,则有:
[[1],
[1,1],
[1,2,1],
…
假设要打印n行,
对于特点2,则有:
L[i][0] = L[i][i] = 1(i = 0,1,2,…,n-1)
对于特点3,则有:
当j != 0且j != i时,L[i][j] = L[i - 1][j - 1] + L[i - 1][j]
首先,初始化一个所有元素都为1的n行二维列表,第i行有i个数
然后,根据上述特点3的条件和公式更新二维列表,对杨辉三角中不为1的位置进行更新
最后,根据杨辉三角的格式打印二维列表
打印每行的内容前,先打印一定数量的水平制表符,第i行打印n - i个
打印每行的内容时,除最后一个数之外,每打印一个数之后打印两个水平制表符
对于每行的最后一个数,打印之后换行,准备打印下一行
# 首先,初始化一个所有元素都为1的n行二维列表,第i行有i个数
L = [[1 for j in range(i + 1)] for i in range(9)]
import pprint
pprint.pprint(L)
[[1],
[1, 1],
[1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1]]
# 然后,根据上述特点3的条件和公式更新二维列表,对杨辉三角中不为1的位置进行更新
for i in range(2, 9):
for j in range(i + 1):
if j != 0 and j != i:
L[i][j] = L[i - 1][j - 1] + L[i - 1][j]
import pprint
pprint.pprint(L)
[[1],
[1, 1],
[1, 2, 1],
[1, 3, 3, 1],
[1, 4, 6, 4, 1],
[1, 5, 10, 10, 5, 1],
[1, 6, 15, 20, 15, 6, 1],
[1, 7, 21, 35, 35, 21, 7, 1],
[1, 8, 28, 56, 70, 56, 28, 8, 1]]
# 最后,根据杨辉三角的格式打印二维列表
for i in range(9):
# 打印每行的内容前,先打印一定数量的水平制表符,第i行打印n - i个
print('t' * (8 - i), end = '')
#打印每行的内容时
for j in range(i + 1):
# 除最后一个数之外
if j != i:
# 每打印一个数之后打印两个水平制表符
print('%dtt' % L[i][j], end = '')
# 对于每行的最后一个数,打印之后换行,准备打印下一行
else:
print('%d' % L[i][j])
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
八.谁在说谎
【问题描述】
张三说李四在说谎,李四说王五在说谎,王五说张三和李四都在说谎。
这三人中到底谁说的时真话,谁说的是假话?
【设计思路】
张三说李四在说谎,说明:要么张三说的是真话李四说的是假话,要么张三说的是假话李四说的是真话。
李四说王五在说谎,说明:要么李四说的是真话王五说的是假话,要么李四说的是假话王五说的是真话。
王五说张三和李四都在说谎,说明:要么王五说的是真话张三和李四说的都是假话,要么王五说的是假话张三和李四至少有一个说的是真话。
设True表示某人说的是真话,设False表示某人说的是假话。
设isZhang、isLi和isWang分别表示张三、李四和王五是否在说谎,则其取值范围都为[True,False]
通过三重循环穷举isZhang、isLi和isWang,在穷举的过程中,只要满足已知条件:
isZhang == (not isLi)
and isLi == (not isWang)
and isWang == ((not isZhang) and (not isLi))
即找到谁在说谎
t = [True, False]
for isZhang in t:
for isLi in t:
for isWang in t:
if isZhang == (not isLi)
and isLi == (not isWang)
and isWang == ((not isZhang) and (not isLi)):
print('张三:{zhang}, 李四:{li}, 王五:{wang}'
.format(zhang = '真话' if isZhang == True else '假话',
li = '真话' if isLi == True else '假话',
wang = '真话' if isWang == True else '假话'))
张三:假话, 李四:真话, 王五:假话
九.猴子吃桃
【问题描述】
猴子第一天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。
第二天早上又将第一天剩下的桃子吃掉一半,又多吃了一个。
以后每天早上都吃了前一天剩下的一半后又多吃了一个。
到第10天早上想再吃时,发现只剩下一个桃子了。
求猴子第一天共摘下了多少个桃子。
【设计思路】
设计思路一:递推
第1天的桃子树是第2天的桃子树加1后的2倍,第2天的桃子树是第3天的桃子树加1后的2倍,
……,一般地,第n天的桃子数是第n+1天的桃子树加1后的2倍。
设第n天的桃子数是L(n),则有递推关系L(n)=(L(n+1)+1) * 2,且初始条件为:L(10)=1
根据递推关系和初始条件,L(10)–>L(9)–>L(8)……–>L(1).
def monkey_peach1():
L = [None] * 11
L[10] = 1
for n in range(9, 0, -1):
L[n] = (L[n + 1] + 1) * 2
return L[1]
print('猴子第一天共摘了%d个桃子' % monkey_peach1())
猴子第一天共摘了1534个桃子
设计思路二:递归
设计思路一的递推关系可看做在一个函数体的内部又调用了该函数。
设计思路二的初始条件可看做递归结束条件(递归出口)
def monkey_peach2(day):
if day == 10:
return 1
else:
return(monkey_peach2(day + 1) + 1) * 2
print('猴子第一天共摘了%d个桃子' % monkey_peach2(1))
猴子第一天共摘了1534个桃子
十.汉诺塔
【问题描述】
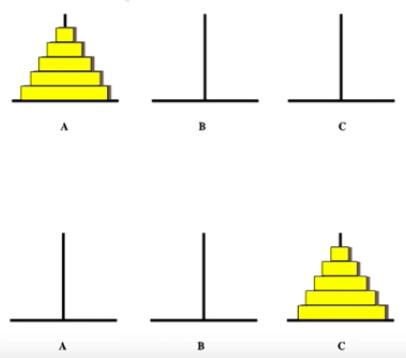
有一个梵塔叫汉诺塔,汉诺塔上有三根柱子A、B和C,
柱子A上有若干圆盘,所有圆盘大小不等,且小的在大的在下。
将柱子A上的所有圆盘借助柱子B移动到柱子C上,移动的过程中每次只能移动一个圆盘,
移动后仍然是小的在上大的在下,如下图所示:
求汉诺塔的三根柱子上所有圆盘的移动过程。
【设计思路】
当柱子A上有2个圆盘时,先将柱子A上面的圆盘从柱子A移动到柱子B,
再将柱子A下面的圆盘从柱子A移动到柱子C,最后将柱子B的圆盘从柱子B移动到柱子C。
当柱子A有三个圆盘时,先将柱子A上面的两个圆盘从柱子A借助柱子C移动到柱子B,
然后将柱子A最下面的圆盘从柱子A移动到柱子C,最后将柱子B的两个圆盘从柱子B借助柱子A移动到柱子C。
一般地,当柱子A有n个圆盘时,从上到下依次编号为1,2,3……n,
先将柱子A上面编号为1至n-1的圆盘从柱子A借助柱子C移动到柱子B,
然后将柱子A最下面编号为n的圆盘从柱子A移动到柱子C,
最后将柱子B的n-1个圆盘从柱子B借助柱子A移动到柱子C。
所求的问题是:将柱子A的n个圆盘借助柱子B移动到柱子C。
结合上面的一般性步骤,很容易想到使用递归。
假设递归函数hanoi(n,A,B,C)用于将n个圆盘从柱子A借助柱子B移动到柱子C,
函数move(m,A,C)用于将编号为m的圆盘从柱子A移动到柱子C,
则上面的一般性步骤可以表示为:
1.当n=1时,调用move(1,A,C),将圆盘从柱子A移动到柱子C。
2.当n>1时,
1).调用hanoi(n-1,A,C,B)
2).调用move(n,A,C),将柱子A最下面编号为n的圆盘从柱子A移动到柱子C;
3).调用hanoi(n-1,B,A,C),将柱子B的n-1个圆盘从柱子B借助柱子A移动到柱子C
from IPython.display import Image
Image(filename = 'F:/Jupyter/Python/lizi1.jpg', width=300, height=150)
def move(m, A, C):
print('移动%d号圆盘,%s ---> %s' % (m, A, C))
def hanoi(n, A, B, C):
if n == 1:
move(1, A, C)
else:
hanoi(n - 1, A, C, B)
move(n, A, C)
hanoi(n - 1, B, A, C)
hanoi(5, 'A', 'B', 'C')
移动1号圆盘,A ---> C
移动2号圆盘,A ---> B
移动1号圆盘,C ---> B
移动3号圆盘,A ---> C
移动1号圆盘,B ---> A
移动2号圆盘,B ---> C
移动1号圆盘,A ---> C
移动4号圆盘,A ---> B
移动1号圆盘,C ---> B
移动2号圆盘,C ---> A
移动1号圆盘,B ---> A
移动3号圆盘,C ---> B
移动1号圆盘,A ---> C
移动2号圆盘,A ---> B
移动1号圆盘,C ---> B
移动5号圆盘,A ---> C
移动1号圆盘,B ---> A
移动2号圆盘,B ---> C
移动1号圆盘,A ---> C
移动3号圆盘,B ---> A
移动1号圆盘,C ---> B
移动2号圆盘,C ---> A
移动1号圆盘,B ---> A
移动4号圆盘,B ---> C
移动1号圆盘,A ---> C
移动2号圆盘,A ---> B
移动1号圆盘,C ---> B
移动3号圆盘,A ---> C
移动1号圆盘,B ---> A
移动2号圆盘,B ---> C
移动1号圆盘,A ---> C
学习参考:
- 图解Python: http://e-learning.51cto.com/course/12803
- Python菜鸟教程:https://www.runoob.com/python/python-tutorial.html
最后
以上就是着急跳跳糖最近收集整理的关于Learn_Python_例子练习13的全部内容,更多相关Learn_Python_例子练习13内容请搜索靠谱客的其他文章。








发表评论 取消回复