求解数组中的逆序对并优化时间复杂度

数组中的逆序对

题目描述

有一组数，对于其中任意两个数组，若前面一个大于后面一个数字，则这两个数字组成一个逆序对。请设计一个高效的算法，计算给定数组中的逆序对个数。

给定一个int数组A和它的大小n，请返回A中的逆序对个数。保证n小于等于5000。

暴力破解

遍历每一个数，比较这个数和它后面的，出现逆序情况计数器就 + 1。

import java.util.*;

public class Main {
	public int count(int[] A,int n) {
		int cnt = 0;
		int len = A.length();
		for (int i = 0; i < len; ++i) {
			for (int j = i + 1; j < len; ++j) {
				if (arr[i] > arr[j]) {
					cnt++;
				}
			}
		}
		return cnt;
	}
}

很明显这种做法假设数组中有 n 个数字，每个数字都要和 O(n) 个数字比较，因此算法的时间复杂度是 O(n^2)。这个显然不够优。

分支思想来优化

以数组 {7，5，6，4} 为例来分析统计逆序对的过程。每次扫描到一个数字的时候。我们不能拿它和后面的每一个数字做比较。否则时间复杂度还是 O(n^2),所以其实可以考虑只比较两个相邻的数字。

逆序对的总数 = 左边数组中的逆序对的数量 + 右边数组中逆序对的数量 + 左右结合成新的顺序数组时出现的逆序对数。

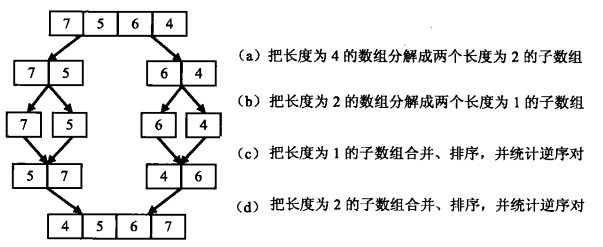
如上图的过程（c）所示，需要注意的是一旦统计了，比如 {7，5} 是一对，就必须对他们排序，防止在以后的统计中再重复统计。

在（d）中合并两个子数组并统计逆序对的具体过程 如下：

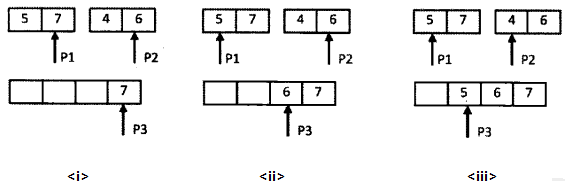
P1 和 P2 分别指向数组最后一个数 (因为在此之前两个长度为 2 的数组已经排好序了，并且统计过逆序对了，所以最后一个数都是两边最大的)。

在 中，P1 大于 P2 ，因此第二个数组中的两个数都比 P1 小，也就是逆序对数 +2，并把 7 复制到辅助数组，向前移动 P1 和 辅助数组的 P3。

在 中，P1 小于当前的 P2，没有逆序对，把当前的 P2 复制到辅助数组即 P3 的位置，并向前移动 P2 和 P3。

在 中，P1 大于当前 P2，存在逆序对，由于当前 P2 是数组中的最后一个数字，也就只可能有一个比 P1 小的，把逆序对 +1，并把 P1 复制到辅助数组，即 P3 的位置，此时 P3 前移，由于 P1 所指的数组已经为空了，所以可以直接按顺序把 P2 所指数组中的值复制到辅助数组。

小结统计两个长度为 2 的子数组之间逆序对的过程

用了两个指针分别指向两个数组的末尾，每次比较这两个对应的数字。如果第一个子数组中的数字大于第二份子数组的数字，则构成逆序对，并且逆序对的数组等于第二个数组中剩余数字的个数；如果第一个数组中的数字小于或等于第二个数组的数字，不构成逆序对。

每一次比较结束的时候，都把较大的数字从后往前复制到辅助数组，确保数字递增排序。复制过后，还要把对应的指针往前移动一位进行下一轮。

详细代码

其实上面的排序过程就是归并排序，可以基于归并排序写出代码

import java.util.*;

public class AntiOrder {
	public int count(int[] A,int n) {
		if (A == null || n == 0) {
			return 0;
		}
		return mergeSortRecursion(A,0,n-1);
	}
	
	public static int mergeSortRecursion(int[] arr,int l, int r) {
		if (l == r) {
			return 0;
		}
		int mid = (l + r) / 2;
		// 逆序对总数 = 左边数组中逆序对 + 右边 + 左右结合成新顺序数组逆序对数量
		return mergeSortRecursion(arr,l,mid) + mergeSortRecursion(arr,mid+1,r) + merge(arr,l,mid,r);
	}
	
	public static int merge(int[] arr, int left, int mid, int right) {
		int[] temp = new int[right - left + 1];
		int index = 0;
		int i = left;
		int j = mid + 1;
		int inverseNum = 0; // 新增，用来累加数组逆序对
		while (i <= mid && j <= right) {
			if (arr[i] <= arr[j]) {
				temp[index++] = arr[i++];
			} else {
				// 当前一个数组元素大于后一个数组元素时，累加逆序对
				// s[i] > s[j] 推导出 s[i]...s[mid] > s[j]
				inverseNum += (mid - i + 1);
				temp[index++] = arr[j++];
			}
		}
		while (i <= mid) {
			temp[index++] = arr[i++];
		}
		while (j <= right) {
			temp[index++] = arr[j++];
		}
		for (int k = 0; k < temp.length; k++) {
			arr[left++] = temp[k];
		}
		return inverseNum；
	}
}

最后

以上就是贤惠小天鹅为你收集整理的求解数组中的逆序对并优化时间复杂度的全部内容，希望文章能够帮你解决求解数组中的逆序对并优化时间复杂度所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。