ACM-ICPC 2018 沈阳赛区网络预赛 F. Fantastic Graph (有上下界可行流)

传送门：https://nanti.jisuanke.com/t/31447

题意：

  一个二分图，左边有n个点，右边有m个点，一共有k条边分别连接左右两个点，问能否取这k条边中部分边，使得所有点的度数都在l~r范围内。

思路：

  有上下界可行流。

建图方法：

  建立一个附加源点ss和附加汇点tt，以及源点s汇点t。

  这里假设上界为r，下界为l。

  对于每条有上下界限制的<u,v>，题目中为<s,x>，<y,t>，做3条边(括号里为容量)<ss,v>(l)，<u,tt>(l)，<u,v>(r-l)。其中前2条边称为附加边，第3条边称为自由边。

  对于没有下界限制的<u,v>，题目中为<x,y>，分别做一条容量为1的边。

  最后由于原图是有源汇的图，因此需要做一条<t,s>(INF)使其转换为无源汇图。

  建图大致如下图所示，其中红线蓝线分别表示一组有上下界限制的<u,v>。

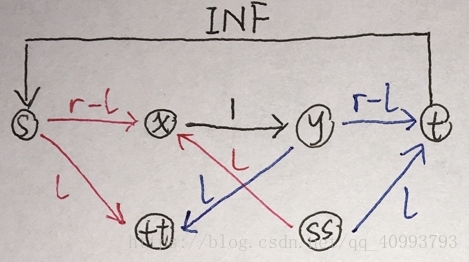
  建完图后，以ss为源点，tt为汇点跑一遍最大流，若等于(n+m)*l（也就是附加边全部满流），则存在可行流。

AC代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cstdlib>
#include<utility>
#include<algorithm>
#include<utility>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<cmath>
#include<map>
#include<ctime>
#include<functional>
#include<bitset>
#define P pair<int,int>
#define ll long long
#define ull unsigned long long
#define lson id*2,l,mid
#define rson id*2+1,mid+1,r
#define ls id*2
#define rs id*2+1
#define Mod(a,b) a<b?a:a%b+b
using namespace std;

const ll M = 998244353;
const ll INF = 1e9 + 10;
const int N = 4010;
const double e = 10e-6;
const int dx[4] = { 0,0,1,-1 }, dy[4] = { 1,-1,0,0 };
const int _dx[8] = { -1,-1,-1,0,0,1,1,1 }, _dy[8] = { -1,0,1,-1,1,-1,0,1 };

struct edge { int to; ll cap; int rev; };
vector<edge>G[N];
int level[N], iter[N];
void addEdge(int from, int to, ll cap)
{
	G[from].push_back(edge{ to,cap,(int)G[to].size() });
	G[to].push_back(edge{ from,0,(int)G[from].size() - 1 });
}
void init()
{
	for (int i = 0; i < N; i++)
		G[i].clear();
}
void bfs(int s)
{
	memset(level, -1, sizeof(level)); level[s] = 0;
	queue<int> que; que.push(s);
	while (!que.empty()) {
		int v = que.front(); que.pop();
		for (int i = 0; i < G[v].size(); i++) {
			edge &e = G[v][i];
			if (e.cap > 0 && level[e.to] < 0) {
				level[e.to] = level[v] + 1;
				que.push(e.to);
			}
		}
	}
}
ll dfs(int v, int t, ll f)
{
	if (v == t) return f;
	int len = G[v].size();
	for (int &i = iter[v]; i < len; i++) {
		edge &e = G[v][i];
		if (e.cap > 0 && level[v] < level[e.to]) {
			ll d = dfs(e.to, t, min(f, e.cap));
			if (d > 0) {
				e.cap -= d;
				G[e.to][e.rev].cap += d;
				return d;
			}
		}
	}
	return 0;
}
ll maxFlow(int s, int t)
{
	ll flow = 0;
	while (1) {
		bfs(s);
		if (level[t] < 0) return flow;
		memset(iter, 0, sizeof(iter));
		ll f;
		while ((f = dfs(s, t, INF)) > 0)
			flow += f;
	}
}

int x, y;

int n, m, k, l, r;

int main()
{
	int cas = 1;
	while (~scanf("%d%d%d", &n, &m, &k)) {
		init();
		int ss = 0, tt = n + m + 3;
		int s = n + m + 1, t = n + m + 2;
		scanf("%d%d", &l, &r);
		while (k--) {
			scanf("%d%d", &x, &y);
			addEdge(x, y + n, 1);
		}
		addEdge(t, s, INF);
		for (int i = 1; i <= n; i++) {
			addEdge(s, i, r - l);
			addEdge(ss, i, l);
			addEdge(s, tt, l);
		}
		for (int i = 1; i <= m; i++) {
			addEdge(i + n, t, r - l);
			addEdge(i + n, tt, l);
			addEdge(ss, t, l);
		}
		printf("Case %d: ", cas++);
		if (maxFlow(ss, tt) == (n + m)*l)
			puts("Yes");
		else
			puts("No");
	}
	return 0;
}

最后

以上就是知性高跟鞋为你收集整理的ACM-ICPC 2018 沈阳赛区网络预赛 F. Fantastic Graph (有上下界可行流)的全部内容，希望文章能够帮你解决ACM-ICPC 2018 沈阳赛区网络预赛 F. Fantastic Graph (有上下界可行流)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。