数据结构------最短路弗洛伊德算法（Flody)一、Foldy代码核心介绍总结

50 阅读 0 评论 33 点赞

我是靠谱客的博主聪慧菠萝，最近开发中收集的这篇文章主要介绍数据结构------最短路弗洛伊德算法（Flody)一、Foldy代码核心介绍总结，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

前言

一、Foldy代码核心介绍

二、Flody代码详解：

三、所有代码：

四、 Foldy算法分析:

总结

前言

如果你要求所有顶点至所有顶点的最短路径问题时，弗洛伊德算法是非常不错的选择。因为它十分简洁。

一、Foldy代码核心介绍

(1) 两个二维数组D[v][w] 和P[v][w]，分别存最短距离和最短路径。

(2) D[v][w] = min(D[v,w] ，D[v][k]+D[k][w])

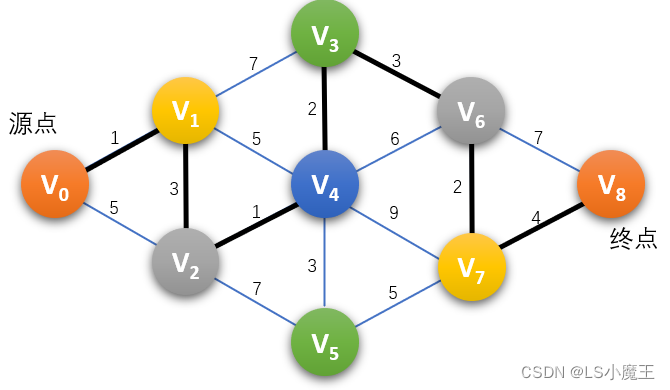
二、Flody代码详解：

/*Floyd算法，求网图G中各顶点v到其余顶点w的最短路径P[v][w]及带权长度D[v][w]*/
void ShortestPath_Floyd(MGraph G,Patharc*P,ShortPathTable* D)
{
	int v, w, k;
	/*初始化D与P*/
	for (v = 0; v < G.numVertexes; v++)
	{
		for (w = 0; w < G.numVertexes; w++)
		{
			(*D)[v][w] = G.arc[v][w];
			(*P)[v][w] = w;
		}
	}
	
	for (k = 0; k < G.numVertexes; k++)
	{
		for (v = 0; v < G.numVertexes; v++)
		{
			for (w = 0; w < G.numVertexes; w++)
			{
				if ((*D)[v][w] > ((*D)[v][k] + (*D)[k][w]))/*如果v->k->w比v->w更短*/
				{
					(*D)[v][w] = (*D)[v][k] + (*D)[k][w];/*更改v->w最小值*/
					(*P)[v][w] = (*P)[v][k];/* 路径设置为经过下标为k的顶点 */
				}
			}
		}
	}
}

三、所有代码：

#include <iostream>
using namespace std;
#define GRAPH_INFINTY 65535
#define MAXVEX 20
#define MAXEDGE 20
typedef struct {
	int vexs[MAXVEX];
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}MGraph;
typedef int Patharc[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];
/*构造图*/
void CreateGraph(MGraph* G)
{
	int i, j;
	/*初始化顶点数和边数*/
	G->numVertexes = 9;
	G->numEdges = 16;
	/*初始化图的顶点编号*/
	for (i = 0; i < G->numVertexes; i++)
	{
		G->vexs[i] = i;
	}
	/*初始化矩阵*/
	for (i = 0; i < G->numVertexes; i++)
	{
		for (j = 0; j < G->numVertexes; j++)
		{
			if (i == j)
				G->arc[i][j] = 0;
			else
				G->arc[i][j] = GRAPH_INFINTY;
		}
	}
	G->arc[0][1] = 1;
	G->arc[0][2] = 5;
	G->arc[1][2] = 3;
	G->arc[1][3] = 7;
	G->arc[1][4] = 5;

	G->arc[2][4] = 1;
	G->arc[2][5] = 7;
	G->arc[3][4] = 2;
	G->arc[3][6] = 3;
	G->arc[4][5] = 3;

	G->arc[4][6] = 6;
	G->arc[4][7] = 9;
	G->arc[5][7] = 5;
	G->arc[6][7] = 2;
	G->arc[6][8] = 7;

	G->arc[7][8] = 4;


	for (i = 0; i < G->numVertexes; i++)
	{
		for (j = i; j < G->numVertexes; j++)
		{
			G->arc[j][i] = G->arc[i][j];
		}
	}

}
/*Floyd算法，求网图G中各顶点v到其余顶点w的最短路径P[v][w]及带权长度D[v][w]*/
void ShortestPath_Floyd(MGraph G,Patharc*P,ShortPathTable* D)
{
	int v, w, k;
	/*初始化D与P*/
	for (v = 0; v < G.numVertexes; v++)
	{
		for (w = 0; w < G.numVertexes; w++)
		{
			(*D)[v][w] = G.arc[v][w];
			(*P)[v][w] = w;
		}
	}
	
	for (k = 0; k < G.numVertexes; k++)
	{
		for (v = 0; v < G.numVertexes; v++)
		{
			for (w = 0; w < G.numVertexes; w++)
			{
				if ((*D)[v][w] > ((*D)[v][k] + (*D)[k][w]))/*如果v->k->w比v->w更短*/
				{
					(*D)[v][w] = (*D)[v][k] + (*D)[k][w];/*更改v->w最小值*/
					(*P)[v][w] = (*P)[v][k];/* 路径设置为经过下标为k的顶点 */
				}
			}
		}
	}
}
int main()
{
	int v, w;
	MGraph G;
	Patharc P;
	ShortPathTable D;
	CreateGraph(&G);
	ShortestPath_Floyd(G, &P, &D);
	cout << "各顶点间最短路径如下" << endl;
	for (v = 0; v < G.numVertexes; v++)
	{
		for (w = v+1; w < G.numVertexes; w++)
		{
			int j = G.vexs[v];
			cout << G.vexs[v] << " -> " << G.vexs[w] << " weight: "<<D[v][w]<<"  path: "<<G.vexs[v];
			while (j!=w)
			{
				cout << " -> " << P[j][w];
				j = P[j][w];
			}
			cout << endl;
		}
		cout << endl;
	}

	return 0;
}