Robotic Sort

Somewhere deep in the Czech Technical University buildings, there are laboratories for examining mechanical and electrical properties of various materials. In one of yesterday’s presentations, you have seen how was one of the laboratories changed into a new multimedia lab. But there are still others, serving to their original purposes. 

In this task, you are to write software for a robot that handles samples in such a laboratory. Imagine there are material samples lined up on a running belt. The samples have different heights, which may cause troubles to the next processing unit. To eliminate such troubles, we need to sort the samples by their height into the ascending order. 

Reordering is done by a mechanical robot arm, which is able to pick up any number of consecutive samples and turn them round, such that their mutual order is reversed. In other words, one robot operation can reverse the order of samples on positions between A and B. 

A possible way to sort the samples is to find the position of the smallest one (P1) and reverse the order between positions 1 and P1, which causes the smallest sample to become first. Then we find the second one on position P and reverse the order between 2 and P2. Then the third sample is located etc. 



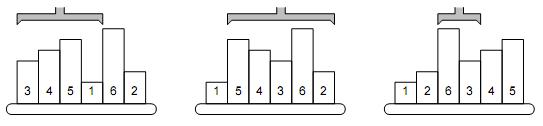
The picture shows a simple example of 6 samples. The smallest one is on the 4th position, therefore, the robot arm reverses the first 4 samples. The second smallest sample is the last one, so the next robot operation will reverse the order of five samples on positions 2–6. The third step will be to reverse the samples 3–4, etc. 

Your task is to find the correct sequence of reversal operations that will sort the samples using the above algorithm. If there are more samples with the same height, their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too.

#include <bits/stdc++.h>
using namespace std;
#define maxn 100005
int pre[maxn], sz[maxn], ch[maxn][2], rev[maxn], rt, tot;
vector<pair<int,int> >g;
bool mySort(pair<int, int> e1, pair<int, int> e2){
if(e1.first == e2.first) return e1.second < e2.second;
return e1.first < e2.first;
}
void newNode(int& r, int fa){
r = ++tot;
pre[r] = fa;
sz[r] = 1;
ch[r][0] = ch[r][1] = 0;
rev[r] = 0;
}
inline void update(int r){
if(!r) return;
swap(ch[r][1], ch[r][0]);
rev[r] ^= 1;
}
inline void pushdown(int r){
if(!r) return;
if(rev[r]){
update(ch[r][1]);
update(ch[r][0]);
rev[r] = 0;
}
}
inline void pushup(int r){
sz[r] = 1 + sz[ch[r][0]] + sz[ch[r][1]];
}
void rotate(int r, int kind){
int y = pre[r];
pushdown(y);
pushdown(r);
ch[y][!kind] = ch[r][kind];
pre[ch[r][kind]] = y;
if(pre[y]){
ch[pre[y]][ch[pre[y]][1] == y] = r;
}
ch[r][kind] = y;
pre[r] = pre[y];
pre[y] = r;
pushup(y);
pushup(r);
}
void splay(int r, int goal){
while(pre[r] != goal){
if(pre[pre[r]] == goal){
rotate(r, ch[pre[r]][0] == r);
}
else{
int y = pre[r];
int kind = ch[pre[y]][0] == y;
if(ch[pre[r]][!kind] == r){
rotate(y, kind);
rotate(r, kind);
}
else{
rotate(r, !kind);
rotate(r, kind);
}
}
}
if(goal == 0) rt = r;
}
void insert(int id){
int r = rt;
while(1){
sz[r]++;
if(id < r){
if(ch[r][0]) r = ch[r][0];
else break;
}
else{
if(ch[r][1]) r = ch[r][1];
else break;
}
}
newNode(ch[r][id >= r], r);
splay(ch[r][id >= r], 0);
}
void remove(){
if(!rt) return;
pushdown(rt);
if(ch[rt][1] == 0){
rt = ch[rt][0];
}
else{
int y = ch[rt][1];
pushdown(y);
while(ch[y][0]){
y = ch[y][0];
pushdown(y);
}
splay(y, rt);
ch[y][0] = ch[rt][0];
pre[ch[rt][0]] = y;
rt = y;
pushup(rt);
}
pre[rt] = 0;
}
int main(){
int n, x;
while(scanf("%d", &n) != EOF && n){
rt = tot = 0;
g.clear();
for(int i = 1; i <= n; ++i){
scanf("%d", &x);
g.push_back(make_pair(x, i));
if(rt == 0){
newNode(rt, 0);
}
else{
insert(i);
}
}
sort(g.begin(), g.end(), mySort);
for(int i = 0; i < g.size() - 1; ++i){
x = g[i].second;
splay(x, 0);
printf("%d ", i + 1 + sz[ch[rt][0]]);
update(ch[rt][0]);
remove();
}
printf("%dn", n);
}
}
/*
题意：1e5个整数，定义一种特殊的排序，每次操作是将第i小的数到下标为i的一段区间整体翻转，每次操作前输出
第i小的这个数的下标。
思路：
平衡树中的翻转操作也是很常见的。类似于线段树中的区间修改操作，用lazy标记区间被修改了，不需要更新到底。
需要往下访问的时候再往下更新，这样可以提高效率，减少重复的更新。
splay中的翻转操作也可以用lazy标记区间被翻转。然后注意在向下访问的时候pushdown一下，否则可能访问到错误的结点。
翻转操作就是将右儿子和左儿子交换一下，然后打个lazy翻转标记。同时在想下访问的时候和rotate的时候注意pushdown
这个标记和维护sz[]数组。
*/

最后

以上就是包容牛排为你收集整理的HDU-1890 Robotic Sort (带翻转、删除操作的splay)Robotic Sort的全部内容，希望文章能够帮你解决HDU-1890 Robotic Sort (带翻转、删除操作的splay)Robotic Sort所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。