递推&&递归

96 阅读 0 评论 64 点赞

我是靠谱客的博主俭朴猫咪，最近开发中收集的这篇文章主要介绍递推&&递归，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

递推&&递归

这两个名词有一点抽象，还是通过例子来具体理解吧。

例题选讲：

题意：

剑指 Offer 10- I. 斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007）

示例 1：

输入：n = 5
输出：5

递推：

class Solution {
    public static int mod = 1000000007;
    public int fib(int n) {
        int[] f = new int[200];
        f[0] = 0;  // 初始值
        f[1] = 1;
        for (int i = 2; i <= n; ++i) // 计算中间过程的值，直到答案出现。
            f[i] = (f[i-1] + f[i-2]) % mod;
        return f[n];
    }
}

就是从问题的边界入手，计算过程中的值，直到得到想要的答案。

也就是一步步的逼近答案。

递归

class Solution {
    public static int mod = 1000000007;
    public int fib(int n) { // 每次调用自己，只是传入的值不一样了。 
        if (n < 2) return n; // 返回边界的值
        return (fib(n-1) + fib(n-2)) % mod;  // 不断的递归调用自己。
    }
}

递归就是不断调用自己的一个过程，如果到达了边界条件就会返回。

本题就是首先询问 n 的答案，但是 n 的答案不知道，所以在此调用自己询问 n-1 n-2 的答案。这样一直调用下去，直到到达边界条件，即 n==0 || n==1的时候,就不会再调用自己了。

递归的两个基本特征就是：

自我调用
终止条件

下图就是递归运行的具体过程。

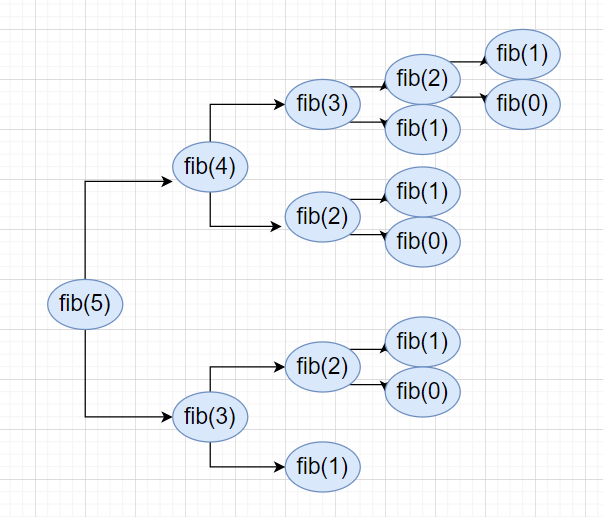
在这里插入图片描述

我们可以看到 fib(2) 调用了好多次，每次又会去访问 fib(0) fib(1)，所以这样会大大的浪费时间，不止是2，对于其他的数也是一样，相同的函数会调用很多次。所以上面的代码如果提交会超时。

如果我们已经得到了 fib(2) 的值，就可以把 fib(2) 的值记录下来，下次如果再访问就直接返回。这样就会很大程度上的节省时间。这个就叫做记忆化。

下面就是优化后的代码。

class Solution {
    public static int[] f = new int[200];
    public static int mod = 1000000007;
    public int fib(int n) {
        if (n < 2) return n;
        if (f[n] != 0) return f[n];  // 如果当前已经有值了，就直接返回。
        return f[n] = (fib(n-1) + fib(n-2)) % mod; // 把 f[n] 的值记录下来，然后返回。
    }
}