二分图又称二部图。
二分图是无向图。
设G=(V,E)是一个无向图。如顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属两个不同的子集。
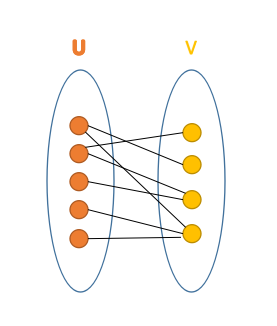
例如这就是一个二分图。 大概就是把顶点分成两堆,每堆内部没有边。
无向图G为二分图的充分必要条件是,G至少有两个顶点, 且其所有回路的长度均为偶数。
最大独立点集:在二分图中,求最少的点集,使得任意两个点之间没有直接边连接。
最小点覆盖:在二分图中,求最少的点集,使得每一条边至少都有端点在这个点集中。
二分图判断:二分图染色。
给一个无向图。要给图上每个顶点染色,并且使任意相邻的顶点染色不同。并且最多用两种颜色。
如果可以进行二分图染色,证明是一个二分图。
如果可以染色,就是如上图,把每一个颜色放入一个堆,就构成了二分图。
模板:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int MAX_V = 205;
vector<int> G[MAX_V]; // 图
int V; // 顶点数
int color[MAX_V]; // 顶点i的颜色 1 或 -1
// 把顶点染成1或-1
bool dfs(int v, int c)
{
color[v] = c; // 把顶点v染成颜色c
for (int i = 0; i < G[v].size(); ++i) {
if (color[G[v][i]] == c) return false;
if (color[G[v][i]] == 0 && !dfs(G[v][i], -c)) return false;
}
return true;
}
void solve()
{
for (int i = 0; i < V; ++i) {
if (color[i] == 0) {
if (!dfs(i, 1)) {
puts("No");
return ;
}
}
}
puts("Yes");
}
int main()
{
int E;
while (scanf("%d%d", &V, &E) == 2) {
int a, b;
for (int i = 0; i < V; ++i) G[i].clear();
memset(color, 0, sizeof color);
for (int i = 0; i < E; ++i) {
scanf("%d%d", &a, &b);
G[a].push_back(b);
G[b].push_back(a);
}
solve();
}
return 0;
}
例:hdu4751
题意:一堆人,每个人单方面认识一些人,希望把这些人分成两堆,使得每一堆的人都相互认识。
题解:把所有不互相认识的人建边,如果是二分图,则可以。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int MAX_V = 105;
bool knows[MAX_V][MAX_V];
vector<int> G[MAX_V];
int V;
int color[MAX_V];
bool dfs(int v, int c)
{
color[v] = c;
for (unsigned i = 0; i < G[v].size(); ++i) {
if (color[G[v][i]] == c) return false;
if (color[G[v][i]] == 0 && !dfs(G[v][i], -c)) return false;
}
return true;
}
void solve()
{
for (int i = 1; i <= V; ++i) {
if (color[i] == 0) {
if (!dfs(i, 1)) {
puts("NO");
return ;
}
}
}
puts("YES");
}
int main()
{
while (~scanf("%d", &V)) {
memset(knows, false, sizeof knows);
for (int i = 0; i <= V; ++i) G[i].clear();
memset(color, 0, sizeof color);
int a;
for (int i = 1; i <= V; ++i) {
while (~scanf("%d", &a) && a)
knows[i][a] = true;
}
for (int i = 1; i <= V; ++i) {
for (int j = i + 1; j <= V; ++j) {
if (!knows[i][j] || !knows[j][i]) {
G[i].push_back(j);
G[j].push_back(i);
}
}
}
solve();
}
return 0;
}
转载于:https://www.cnblogs.com/wenruo/p/5243034.html
最后
以上就是忧伤大炮最近收集整理的关于二分图判断(交叉染色)的全部内容,更多相关二分图判断(交叉染色)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复