CCPC-Wannafly Winter Camp Day8 (Div2, onsite) B：玖凛两开花

66 阅读 0 评论 44 点赞

我是靠谱客的博主合适狗，最近开发中收集的这篇文章主要介绍CCPC-Wannafly Winter Camp Day8 (Div2, onsite) B：玖凛两开花，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目描述

为了拯救重要之人，御原玖音和Rinne Ohara都努力地进行时间机器的研究，为此她们正在学习一些必要的算法。在学习的过程中，她们发现了一个叫做开花（Blossom algorithm，也被称作带花树）的有趣算法。

开花算法可以用来解决一般图最大匹配问题，经过一些修改还可以用来解决一般图最大权匹配问题。原始的开花算法的时间复杂度为O(|V|^2|E|)O(∣V∣2∣E∣)，其中|V|,|E|∣V∣,∣E∣分别为图的点数与边数。有很多人对开花算法进行了优化，如Gabow在《 Data structures for weighted matching and nearest common ancestors with linking》一文中将一般图最大权匹配的时间复杂度优化到了O(|V|(|E|+|V| log |V|))O(∣V∣(∣E∣+∣V∣log∣V∣))。

本着不重复造轮子的心态，Rinne尝试在线搜索开花算法的代码，但是找到的却都是时间复杂度为O(V^3)O(V3)的实现方式。玖音只好自己写出一份代码，对一道例题跑出结果，然后请你检验她的答案对不对。

玖音的题目是这样的：

给出一张点集为VV，边集为EE的无向图GG，点的编号为00至|V|-1∣V∣−1，边(u,v)(u,v)的权值为min(u,v)min(u,v)。一个边集SS是图的一个匹配当且仅当S subseteq ES⊆E，且forall e_1,e_2 in S bigwedge e_1 neq e_2∀e1,e2∈S⋀e1̸=e2，满足e_1,e_2e1,e2无公共端点。对于一个边集SS，定义W_SWS为SS中所有边的权值的集合。对于一个自然数集WW，定义Mex(W)Mex(W)为最小的不属于WW的自然数。求对于图GG的匹配SS，Mex(W_S)Mex(WS)的最大值是多少。

好心的Rinne为了减少你的负担，将题目的做法告诉了你，你只需要实现一个高效的开花算法即可。当然，如果你已经会做这道题了，就可以不用继续看下去了。Rinne给出的做法是这样的：

对于所有的边e in Ee∈E，若其原本的边权为ww，将其改为2^{|V|-w}2∣V∣−w。求出新图的最大权匹配后，设其权值之和为XX，将其二进制表示中的最低|V|+1∣V∣+1位由高位到低位依次写出来，第一个为00的位的出现位置（从00开始编号）就是答案。要想证明正确性又要花费一些时间，不过Rinne是不会骗你的。

Note：公式渲染修正：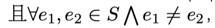

输入描述

第一行两个整数n,m(1 le n le 10 ^4, 1 le m le 2 times 10^4)n,m(1≤n≤104,1≤m≤2×104)，分别代表图的点数与边数。

接下来mm行，每行两个整数u_i,v_i(0 le u_i,v_i < n)ui,vi(0≤ui,vi<n)，代表有一条连接u_i, v_iui,vi的边。保证没有重边和自环。

输出描述

输出共一行一个整数，代表Mex(W_S)Mex(WS)的最大值。

样例输入 1

3 1
1 2

样例输出 1

样例输入 2

样例输出 2

可以发现，如果答案是x，那么小于等于x的点的都要匹配到大于等于x的点，

那么我们把小于x的点放在左边，大于等于x的点放在右边，二分匹配即可

#include <bits/stdc++.h>
using namespace std;
const int maxn= 10010;
int n, m, l, r;
vector <int> G[maxn];
int linker[maxn];
bool used[maxn];
bool DFS(int u)
{
for (auto v : G[u]) if (v >= l && v <= r && !used[v])
{
used[v] = true;
if (linker[v] == -1 || DFS(linker[v]))
{
linker[v] = u;
return true;
}
}
return false;
}
int main()
{
scanf("%d%d",&n,&m);
for (int i = 1, u, v; i <= m; ++i)
{
scanf("%d%d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
int res = 0;
memset(linker, -1, sizeof linker);
for (int i = 0; i < n - 1; ++i)
{
l = i + 1, r = n - 1;
if (linker[i] != -1)
{
memset(used, 0, sizeof used);
if (!DFS(linker[i])) break;
linker[i] = -1;
}
memset(used, 0, sizeof used);
if (DFS(i)) ++res;
else break;
}
printf("%dn", res);
return 0;
}