七大查找算法思想（内含红黑树，B树，B+树分析）

139 阅读 0 评论 92 点赞

我是靠谱客的博主粗暴蜗牛，最近开发中收集的这篇文章主要介绍七大查找算法思想（内含红黑树，B树，B+树分析），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

总结这篇的原因是今天实验室的好几个同学都被问到红黑树的相关问题
于是慌的一批Orz

首先复习一些概念
查找算法分类：
　　1）静态查找和动态查找；
　　　静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。
　　2）无序查找和有序查找。
　　　　无序查找：被查找数列有序无序均可；
　　　　有序查找：被查找数列必须为有序数列。
平均查找长度（Average Search Length，ASL）：需和指定key进行比较的关键字的个数的期望值，称为查找算法在查找成功时的平均查找长度。
　　对于含有n个数据元素的查找表，查找成功的平均查找长度为：ASL = Pi*Ci的和。
　　Pi：查找表中第i个数据元素的概率。
　　Ci：找到第i个数据元素时已经比较过的次数。

1. 顺序查找

基本思想：顺序查找也称为线形查找，属于无序查找算法。从数据结构线形表的一端开始，顺序扫描，依次将扫描到的结点关键字与给定值k相比较，若相等则表示查找成功；若扫描结束仍没有找到关键字等于k的结点，表示查找失败。
最佳使用结构：存储结构为顺序存储或链接存储的线性表。

2.二分查找

基本思想：二分查找也称折半查找，属于有序查找算法。用给定值k先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等则查找成功；若不相等，再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表，这样递归进行，直到查找到或查找结束发现表中没有这样的结点。
最佳使用结构：顺序存储的有序表。

3.插值查找

基本思想：基于二分查找算法，将查找点的选择改进为自适应选择（mid=low+(key-a[low])/(a[high]-a[low])*(high-low)），可以提高查找效率。当然，差值查找也属于有序查找。
最佳使用结构：表长较大，而关键字分布又比较均匀的查找表。

4.斐波那契查找

基本思想：二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。

斐波那契查找与折半查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1，及n=F(k)-1;

开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种

1）相等，mid位置的元素即为所求

2）>，low=mid+1,k-=2;

说明：low=mid+1说明待查找的元素在[mid+1,high]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个。

3）<，high=mid-1,k-=1。

说明：low=mid+1说明待查找的元素在[low,mid-1]范围内，k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个。

5. 树表查找

二叉查找树
基本思想：二叉查找树是先对待查找的数据进行生成树，确保树的左分支的值小于右分支的值，然后在就行和每个节点的父节点比较大小，查找最适合的范围。这个算法的查找效率很高，但是如果使用这种查找方法要首先创建树。
二叉查找树满足：
1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2）若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3）任意节点的左、右子树也分别为二叉查找树。
4）对二叉查找树进行中序遍历，即可得到有序的数列。
=====================================================================
平衡查找树之2-3树
2树：保存一个key(value)，和两个指向左右的节点，左节点也是一个2-3节点，所有的值都比key要小，右节点也是一个2-3节点，所有的值比key要大。
3树：保存两个key(value)，和三个指向左中右的节点，左节点也是一个2-3节点，所有的值均比两个key中的最小的key还要小；中间节点也是一个2-3节点，中间节点的key值在两个跟节点key值之间；右节点也是一个2-3节点，节点的所有key值比两个key中的最大的key还要大。

2-3树性质：
1）如果中序遍历2-3查找树，就可以得到排好序的序列；
2）在一个完全平衡的2-3查找树中，根节点到每一个为空节点的距离都相同。

=====================================================================
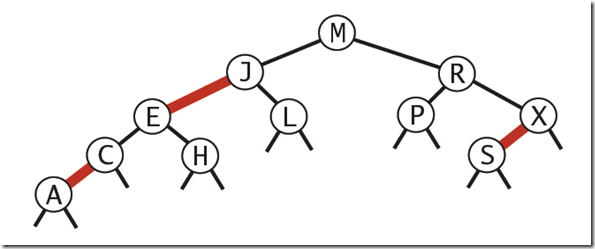
平衡查找树之红黑树
基本思想：红黑树的思想就是对2-3查找树进行编码，尤其是对2-3查找树中的3-nodes节点添加额外的信息。红黑树中将节点之间的链接分为两种不同类型，红色链接用来链接两个2-nodes节点来表示一个3-nodes节点。黑色链接用来链接普通的2-3节点。特别的，使用红色链接的两个2-nodes来表示一个3-nodes节点，并且向左倾斜，即一个2-node是另一个2-node的左子节点。这种做法的好处是查找的时候不用做任何修改，和普通的二叉查找树相同。

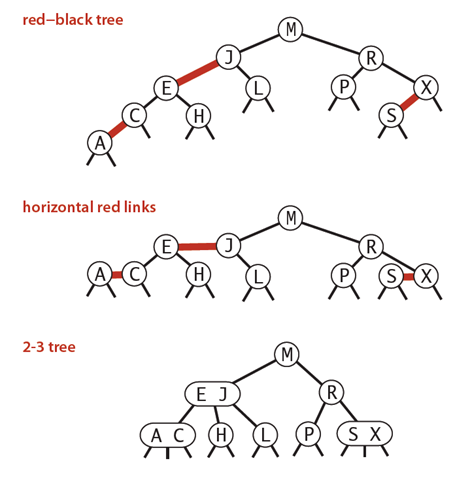
红黑树性质：
1）整个树完全黑色平衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同（即2-3树的从根节点到叶子节点的距离都相等）。
2）红色节点向左倾斜，一个节点不可能有两个红色链接。

=====================================================================
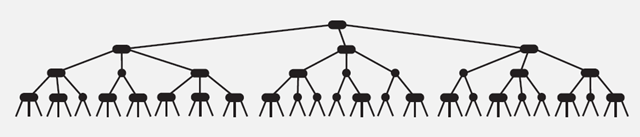
平衡查找树之B树
B树是一个节点可以拥有多于2个子节点的二叉查找树。与自平衡二叉查找树不同，B树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程，从而加快存取速度。普遍运用在数据库和文件系统。

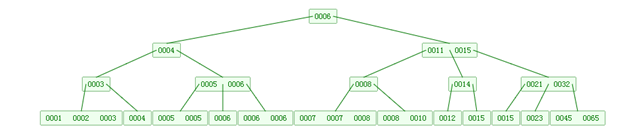
B树性质：
M是B树的阶数
1）B树可以看作是对2-3查找树的一种扩展，即他允许每个节点有M-1个子节点。
2）根节点至少有两个子节点
3）每个节点有M-1个key，并且以升序排列
4）位于M-1和M key的子节点的值位于M-1 和M key对应的Value之间
5）其它节点至少有M/2个子节点
B树优点：由于B树的每一个节点都包含key和value，因此经常访问的元素可能离根节点更近，因此访问也更迅速。
=====================================================================
平衡查找树之B+树
B+树是对B树的一种变形树，它与B树的差异在于：
1）有k个子结点的结点必然有k个关键码；
2）非叶结点仅具有索引作用，跟记录有关的信息均存放在叶结点中。
3）树的所有叶结点构成一个有序链表，可以按照关键码排序的次序遍历全部记录。

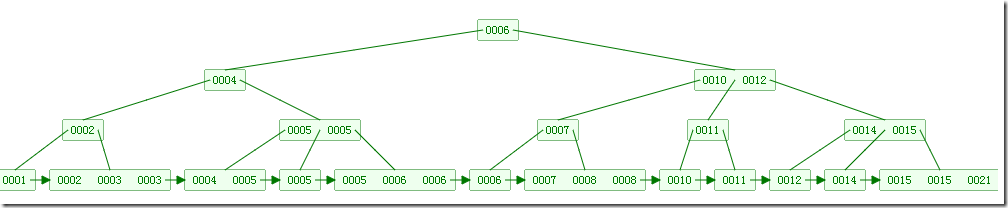
B+树优点：
1）由于B+树在内部节点上不好含数据信息，因此在内存页中能够存放更多的key。数据存放的更加紧密，具有更好的空间局部性。因此访问叶子几点上关联的数据也具有更好的缓存命中率。
2）B+树的叶子结点都是相链的，因此对整棵树的便利只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻，所以缓存命中性没有B+树好。
B树与B+树对比图：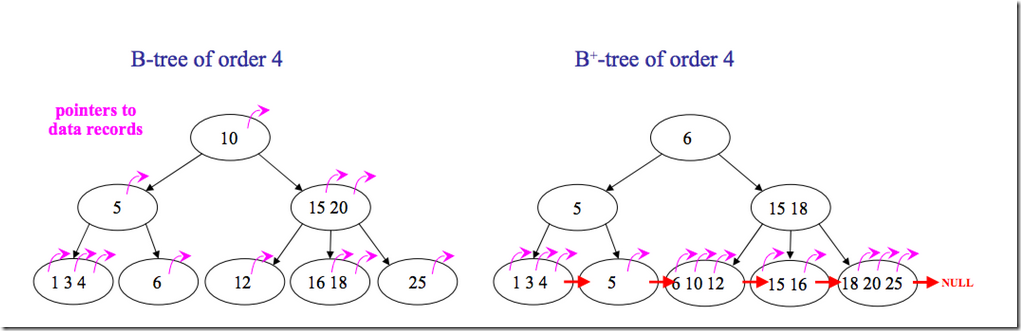

6.分块查找

基本思想：即索引顺序查找。将n个数据元素"按块有序"划分为m块（m ≤ n）。每一块中的结点不必有序，但块与块之间必须"按块有序"；即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都必须小于第3块中的任一元素，……
算法流程：
1）先选取各块中的最大关键字构成一个索引表；
2）查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；然后，在已确定的块中用顺序法进行查找。

7.哈希查找

基本思想：如果所有的键都是整数，那么就可以使用一个简单的无序数组来实现：将键作为索引，值即为其对应的值，这样就可以快速访问任意键的值。这是对于简单的键的情况，我们将其扩展到可以处理更加复杂的类型的键。
算法流程：
1）用给定的哈希函数构造哈希表。
2）根据选择的冲突处理方法解决地址冲突（拉链法和线性探测法）。
3）在哈希表的基础上执行哈希查找。