1.什么是递归

递归算法在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。
递：将递归问题分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决
归：当你将问题不断缩小规模递去的时候，必须有一个明确的结束递去的临界点（递归出口），一旦达到这个临界点即就从该点原路返回到原点，最终问题得到解决。

1.1.递归过程

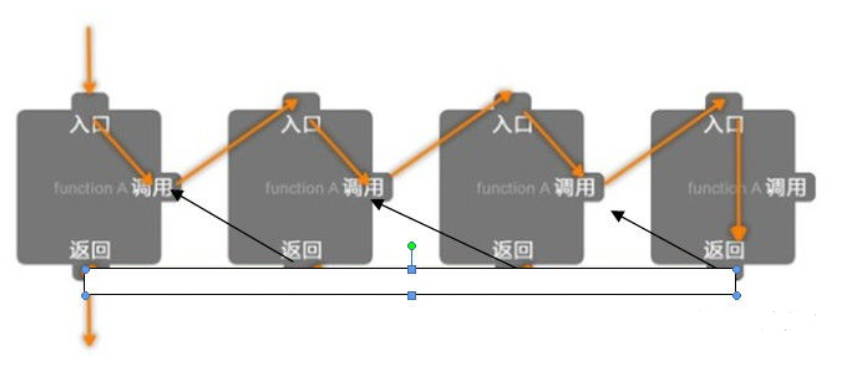
1.2.运用递归的场景

具有以下特征的问题可考虑递归求解：
当问题和子问题具有递推关系，比如杨辉三角、计算阶乘。
具有递归性质的数据结构，比如链表、树、图。
反向性问题，比如取反。
总结下来，最根本的还是要抓住问题本身是否可以通过层层拆解到最小粒度来得解。

2.递归的三要素

2.1.定义函数（明确函数的功能）

定义一个函数，明确该函数的功能是什么。

// 算 n 的阶乘(假设n不为0)
int f(int n){

}

2.2.递归的结束条件

所谓递归，就是会在函数内部代码中，调用这个函数本身，所以，我们必须要找出递归的结束条件，不然的话，会一直调用自己，进入无底洞。也就是说，我们需要找出当参数为多少时，递归结束，之后直接把结果返回，请注意，这个时候我们必须能根据这个参数的值，能够直接知道函数的结果是什么。
如n的阶乘，结束条件为f(1) = 1。

// 算 n 的阶乘(假设n不为0)
int f(int n){
	if(n == 1)
	{
		return 1;
	}
}

2.3.找出函数的等价关系

不断缩小参数的范围，缩小之后，我们可以通过一些辅助的变量或者操作，使原函数的结果不变。

例如，f(n) 这个范围比较大，我们可以让 f(n) = n * f(n-1)。这样，范围就由 n 变成了 n-1 了，范围变小了，并且为了原函数f(n) 不变，我们需要让 f(n-1) 乘以 n。 说白了，就是要找到原函数的一个等价关系式，f(n) 的等价关系式为 n * f(n-1)，即 f(n) = n * f(n-1)。

int f(int n){
	if(n == 1)
	{
		return 1;
	}
	retrun f(n-1)*n;
}

3.案例

3.1.斐波那契数列

斐波那契数列指的是这样一个数列：0、1、1、2、3、5、8、13、21、34。。。。
这个数列从第3项开始，每一项都等于前两项之和。

解题思路：

• 定义函数

	int f(int n);

• 递归结束条件
  当n = 1,2时,f(n) = 1，这个就是递归的结束条件；

• 等价关系
  数列从第3项开始，每一项都等于前两项之和，故f(n) = f(n-1) + f(n -2)

int f(int n)
{
	//结束条件
	if(n <= 2)
	{
		return 1;
	}
	//递归等价公式
	return f(n-1)+f(n-2);
}

3.2.小青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

解题思路：

• 定义函数

int f(int n);

• 递归结束条件
  f(1) = f(0) + f(-1)；
  f(2) = f(1) + f(0)；
  f(0) = 0，按道理是递归结束，不用继续往下调用的，但我们上面的代码逻辑中，会继续调用 f(0) = f(-1) + f(-2)。这会导致无限调用，进入死循环。显然，n=1,2为该递归的结束条件。

• 等价关系
  假设有n级台阶，一次可以跳上1级台阶，也可以跳上2级，则n-1级有f(n-1)种跳法，n-2级有f(n-2)种跳法，n级为n-1级和n-2级跳法的综合，可得f(n) = f(n-1)+f(n-2)。

int f(int n)
{
	if(n<=2)
	{
		return n;
	}
	return f(n-1)+f(n-2);
}

最后

以上就是单身老鼠为你收集整理的五大算法 - 递归算法1.什么是递归2.递归的三要素3.案例的全部内容，希望文章能够帮你解决五大算法 - 递归算法1.什么是递归2.递归的三要素3.案例所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。