1. 首页
  2. 文章中心
  3. 人工智能

感知器与BP神经网络

65 阅读 0 评论
我是靠谱客的博主 搞怪硬币，最近开发中收集的这篇文章主要介绍感知器与BP神经网络，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

文章目录

    • 感知器
      • 一、概念
      • 二、结构图示
      • 三、Matlab代码实现及结果分析
    • BP神经网络
      • 一、概念
      • 二、算法
      • 三、结构图示及公式解析
      • 四、Matlab代码实现及结果分析

感知器

一、概念

感知器是最简单的前向神经网络，主要用于模式分类。感知器只对线性可分的向量集合进行分类。

二、结构图示

单层感知器模型：
单层感知器模型

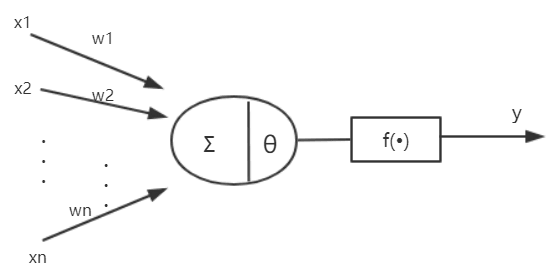
x1,x2, …为感知器的n个输入
w1,w2…为与输入相对应的n个连接权值
θ为阈值
f(•)为激活函数
y为单层感知器的输出

三、Matlab代码实现及结果分析

(一)感知器函数介绍

  • newp函数生成感知器神经网络

net=newp(pr,s,tf,lf)
net:函数返回参数，表示生成的感知器网络
参数pr:输入向量矩阵
参数s:神经元的个数
参数tf:感知器的传递函数,默认hardlim
参数lf:感知器的学习函数，默认learnp

  • train函数进行样本训练

net=train(net,P,T)
参数net:被训练网络
参数P：输入向量
参数T：目标输出

  • learnp函数进行权值和阈值的学习

dW=learnp(W,P,Z,N,A,T,E,D,gW,gA,LP,LS)
dW:权值或阈值增量矩阵
参数W：权值矩阵或阈值向量
参数P：输入向量
参数T：目标向量
参数E：误差向量
其余可忽略，设为[]

（二）感知器神经网络的生成与训练
先生成感知器网络，通过样本训练，确定感知器的权值与阈值。若以t表示目标输出，a表示实际输出，训练的目的就是使t-a经过有限次迭代之后，将收敛到正确的权值与阈值，使e=0。

% 1.1  生成网络
net=newp([0 2],1);%单输入，输入值为[0,2]之间的数
inputweights=net.inputweights{1,1};%第一层的权重为1
biases=net.biases{1};%阈值为1
% 1.2  网络仿真
net=newp([-2 2;-2 2],1);%两个（二维）输入，一个神经元，默认二值激活
net.IW{1,1}=[-1 1];%权重，net.IW{i,j}表示第i层网络第j个神经元的权重向量
net.IW{1,1};
net.b{1}=1;
net.b{1}
p1=[1;1],a1=sim(net,p1)
p2=[1;-1],a2=sim(net,p2)
p3={[1;1] [1 ;-1]},a3=sim(net,p3) %两组数据放一起
p4=[1 1;1 -1],a4=sim(net,p4)%也可以放在矩阵里面
net.IW{1,1}=[3,4];
net.b{1}=[1];
a1=sim(net,p1)
% 1.3  网络初始化
net=init(net);
wts=net.IW{1,1}
bias=net.b{1}
% 改变权值和阈值为随机数
net.inputweights{1,1}.initFcn='rands';
net.biases{1}.initFcn='rands';
net=init(net);%重新初始化
bias=net.b{1}%初始化定义阈值
wts=net.IW{1,1}%初始化定义权值
a1=sim(net,p1)

%2. 感知器神经网络的学习和训练
%1 网络学习
net=newp([-2 2;-2 2],1);
net.b{1}=[0];
w=[1 -0.8]
net.IW{1,1}=w;
p=[1;2];
t=[1];
a=sim(net,p)
e=t-a
%learnp为权值和阈值的学习函数
dw=learnp(w,p,[],[],[],[],e,[],[],[],[],[])
w=w+dw
net.IW{1,1}=w;
a=sim(net,p)%sim为网络仿真函数
net = newp([0 1; -2 2],1);
P = [0 0 1 1; 0 1 0 1];
T = [0 1 1 1];
Y = sim(net,P)
net.trainParam.epochs = 20;%最大训练次数为20
net = train(net,P,T);%P表示输入向量，T表示目标向量
Y = sim(net,P)
 % 2 网络训练
net=init(net);
p1=[2;2];t1=0;p2=[1;-2];t2=1;p3=[-2;2];t3=0;p4=[-1;1];t4=1;
net.trainParam.epochs=1;
net=train(net,p1,t1)
w=net.IW{1,1}
b=net.b{1}
a=sim(net,p1)
net=init(net);
p=[[2;2] [1;-2] [-2;2] [-1;1]];
t=[0 1 0 1];
net.trainParam.epochs=1;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=2;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=20;
net=train(net,p,t);
a=sim(net,p)

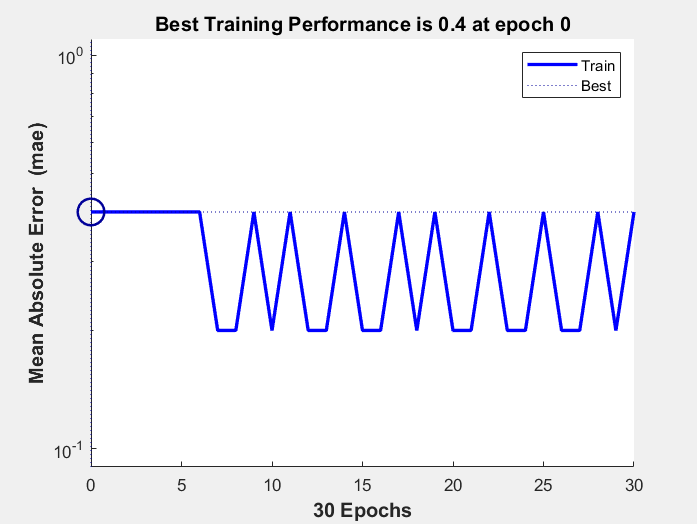
运行结果：
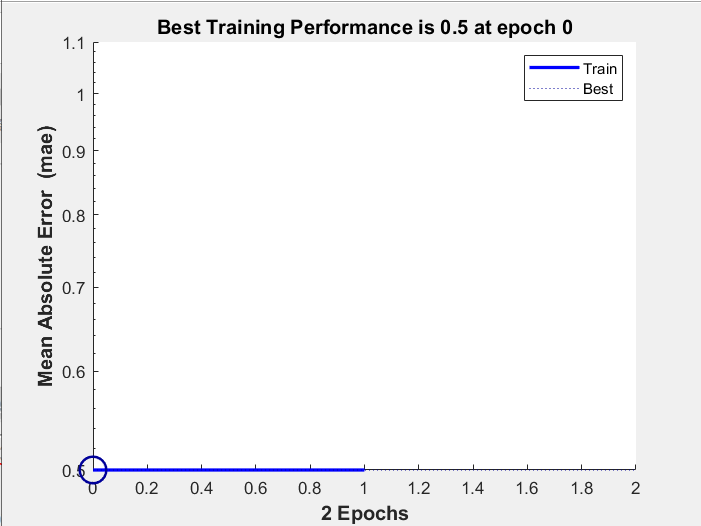
训练相关数据：
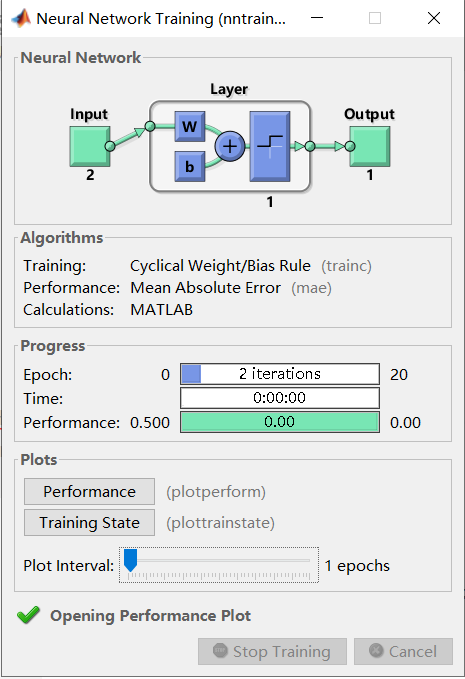
在这里插入图片描述
分析：poch表示迭代次数，此样本中最大次数为20次，Time表示训练时间，Performance为性能指标,此例中为平均绝对误差（mae）（mae为回归模型中一种损失函数）。
在这里插入图片描述
（三）二输入感知器分类可视化问题

 %3. 二输入感知器分类可视化问题
P=[-0.5 1 0.5 -0.1;-0.5 1 -0.5 1];%输入向量
T=[1 1 0 1] %输出向量
net=newp([-1 1;-1 1],1); %生成感知器
plotpv(P,T);  
plotpc(net.IW{1,1},net.b{1});
hold on;
plotpv(P,T);
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1})
net.adaptParam.passes=3;
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpc(net.IW{1},net.b{1})
net.adaptParam.passes=6;
net=adapt(net,P,T)
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1},net.b{1})

plotpc(net.IW{1},net.b{1})
%仿真
a=sim(net,p);
plotpv(p,a)

p=[0.7;1.2]
a=sim(net,p);
plotpv(p,a);
hold on;
plotpv(P,T);
plotpc(net.IW{1},net.b{1})

仿真结果：
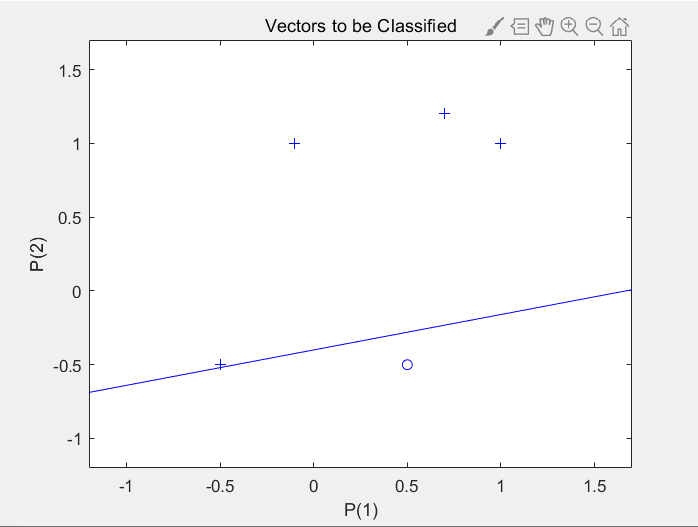
在这里插入图片描述
分析：由图可得分类线将样本分为两类

（四）标准化学习规则训练奇异样本

% 4. 标准化学习规则训练奇异样本
P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1.0 50]
T=[1 1 0 0 1];
net=newp([-40 1;-1 50],1);
plotpv(P,T);%标出所有点
hold on;
linehandle=plotpc(net.IW{1},net.b{1});%画出分类线
E=1;
net.adaptParam.passes=3;%passes决定在训练过程中训练值重复的次数。
while (sse(E))
    [net,Y,E]=adapt(net,P,T);%自适应训练函数
    linehandle=plotpc(net.IW{1},net.b{1},linehandle);
    drawnow;
end;
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%另外一种网络修正学习（非标准化学习规则learnp）
hold off;
net=init(net);
net.adaptParam.passes=3;
net=adapt(net,P,T);
plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%无法正确分类
%标准化学习规则网络训练速度要快！

 % 训练奇异样本
% 用标准化感知器学习规则（标准化学习数learnpn）进行分类
net=newp([-40 1;-1 50],1,'hardlim','learnpn');
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net.adaptParam.passes=3;
net=init(net);
linehandle=plotpc(net.IW{1},net.b{1});
while (sse(e))
[net,Y,e]=adapt(net,P,T);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
end;
axis([-2 2 -2 2]);
net.IW{1}%权重
net.b{1}%阈值
%可正确分类
  1. 未用标准化学习训练结果（分类不正确）：

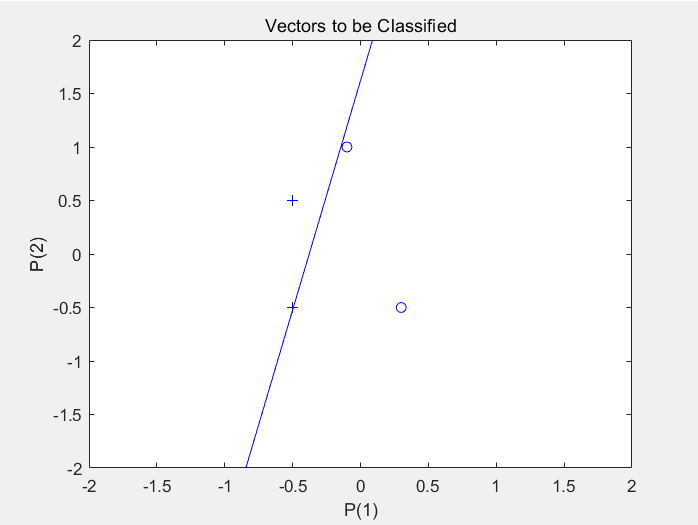
在这里插入图片描述

  1. 标准化学习训练结果（实现正确分类）：

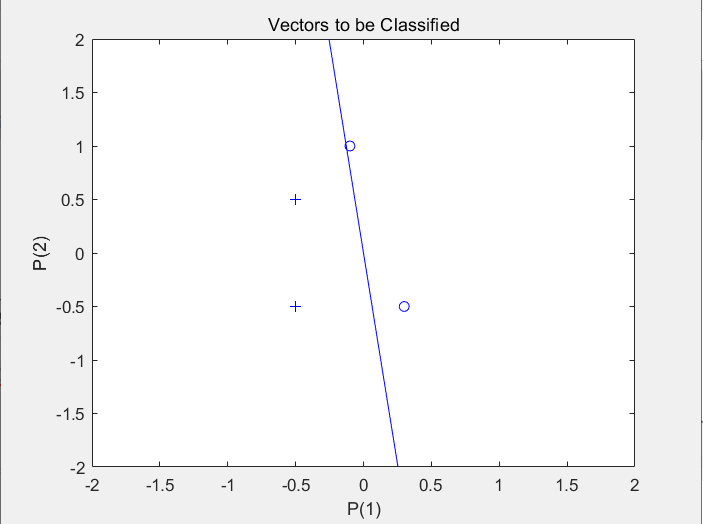
在这里插入图片描述
在这里插入图片描述
（五）多个感知器神经元解决分类问题

 % 5. 设计多个感知器神经元解决分类问题
p=[1.0 1.2 2.0 -0.8; 2.0 0.9 -0.5 0.7]
t=[1 1 0 1;0 1 1 0]
plotpv(p,t);
hold on;
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net=init(net);
while (sse(e))
[net,y,e]=adapt(net,p,t);%自适应训练函数
linehandle=plotpc(net.IW{1},net.b{1},linehandle);%画分类线
drawnow;
end;

训练结果：
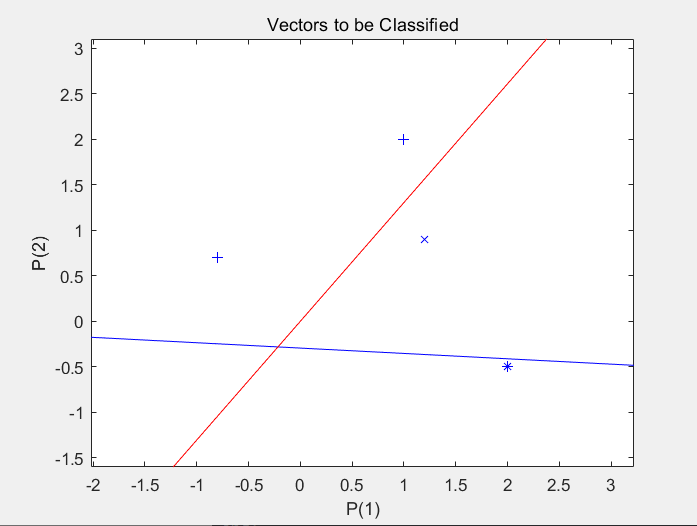
在这里插入图片描述
分析：由图可看出两条分类线清晰的划分出不同类别。

小结：感知器的权值为可变的，这就使得感知器具有可学习的特性。若在输入层和输出层加上多层神经元，可构成多层感知器即多层前向网络。

BP神经网络

一、概念

BP神经网络是根据误差逆传播来训练的多层前馈神经网络。

二、算法

(一)基本思想

BP神经网络学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输人层传入,经过各隐含层逐层处理后,传向输出层。若输出层的实际输出与期望的输出不相等,则转到误差的反向传播过程。误差反向传播是将输出误差以某种形式通过隐含层逐层反传,并将误差分摊给各层的所有神经元,从而获得各层神经元的误差信号,此误差信号作为修正各神经元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程,是周而复始地进行的。权值不断调整的过程,也就是网络的学习训练过程。

(二)算法流程

输入:网络结构参数(层数、结点数等) ;训练数据集 
输出:网络权值与阈值

1.网络权值初始化;
2.对输入训练S={(X1,T1),(X2,T2),…,(Xk,Tk)}；依次通过输入层、隐含层、输出 层,并分别计算误差E:
3.通过误差E反传计算每个神经元的误差信号δ;
4.根据误差信号δ调整网络权值W和结点國值θ;
5.对训练数据不断滚动直至最大滚动次数或误差低于某一阈值为止。

三、结构图示及公式解析

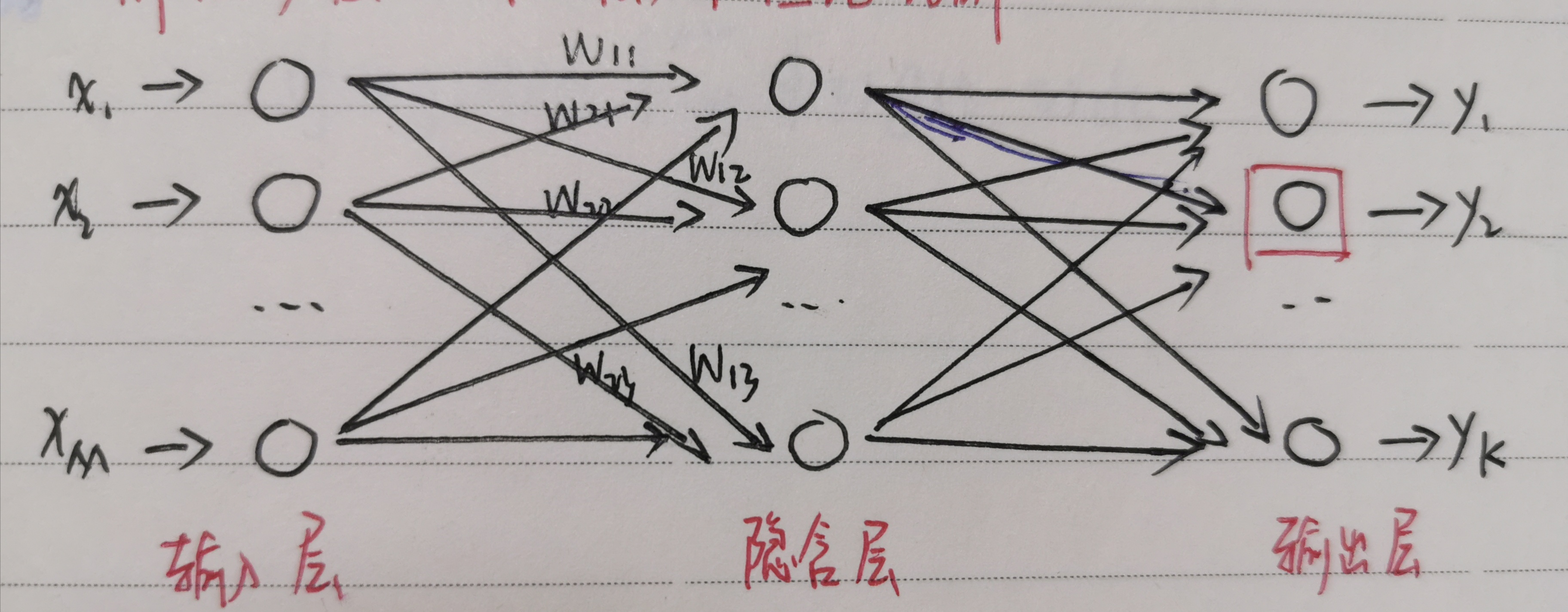
在这里插入图片描述

Xi表示输入
Wij表示权重
Yj表示输出

四、Matlab代码实现及结果分析

（一）函数介绍

  • newff函数
    功能：创建BP网络

net = newfif(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)
P:输入数据矩阵
T:输出数据矩阵
S:隐含层节点数
TF:节点传递函数，包括硬限幅传递函数hardlim,对称硬限幅传递函数hardlims,线性传递函数purelin,正切S型传递函数tansig,对数S型传递函数logsig
BTF:训练函数， ①包括梯度下降BP算法训练函数traingd； ②动量反传的梯度下降BP算法训练函数traingdm；③动态自适应学习率的梯度下降BP算法训练函数traingda, ④动量反传和动态自适应学习率的梯度下降BP算法训练函数traingdx；⑤Levenberg Marquardt的BP算法训练函数trainlm
BLF:网络学习函数，包括①OBP学习规则learngd, ②带动量项的BP学习规则learngdm
PF:性能分析函数，包括均值绝对误差性能分析函数mae, mse
IPF:输入处理函数
OPF:输出处理函数
DDF:验证数据划分函数
一般使用前6个参数，后4个为系统默认参数

  • 神经元激活函数，BP网络常常采用S型对数或者正切函数或线性函数

（1）logsig 函数，S型的对数函数
功能：logsig函数将神经元的输入（范围是整个实数集）映射到区间（0,1）中

A=logsig(N,FP)
info=logsig(code)

N为Q个S维的输入列向量
FP为功能结构参数
A为函数返回值，位于区间（0,1）中

（2）tansig 函数，双曲正切S型传递函数
功能：logsig函数将神经元的输入（范围是整个实数集）映射到区间（-1,1）中

A=tansig(N,FP)
info=logsig(code)

N为Q个S维的输入列向量
FP为功能结构参数
A为函数返回值，位于区间（-1,1）中

（3）purelin 函数 ，线性传递函数
功能：purelin 函数输出等于输入

A = purelin(N,FP)
info = purelin(code)

N为Q个S维的输入列向量
FP为功能结构参数

  • 训练函数-train函数
    功能:用训练数据训练BP神经网络

[net,tr]= train(NET,X,T,Pi,Ai)

net:训练好的网络
tr:训练过程记录
NET:待训练网络
X:输入数据矩阵
T:输出数据知阵
Pi:初始化输入层条件
Ai:初始化输出层条件
一般设置前三个参数，后两个参数用系统默认参数

  • 预测函数-sim函数
    功能:将训练好的BP神经网络预测函数输出

y=sim(net,x)

y:网络预测数据
net:训练好的网络
x:输入的数据

  • 显示函数
    （1）plotes函数
    功能:用来绘制一个单独神经元的误差曲面

plotes(WV,BV,ES,V)

WV:是权值的N维行向量
BV:是M维的阈值行向量
ES:是误差向量组成的M*N维矩阵
V:是视角默认是[-37.5,30]

（2）errsurf函数
功能:用来计算单个神经元的误差曲面

errsurf(P,T,WV,BV,F)

P:是输入行向量
T:是目标行向量
WV:是权值列向量
BV:是阈值列向量
F:是传递函数的名称

(二)BP神经网络创建
代码：

% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}

p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
%net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}

net.IW{1}
net.IW{2}
0.7616+net.b{2}
a-net.b{2}
(a-net.b{2})/ 0.7616
help purelin

p1=[0;0];
a5=sim(net,p1)
net.b{2}
% BP网络
%net=newff([隐层神经元个数，输出层神经元个数]{隐层神经元输出函数，输出层神经元输出函数}，)
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')  % BP神经网络的构建
net.IW{1}
net.b{1}
%p=[1;];
p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}



P=[1.2;3;0.5;1.6]
W=[0.3 0.6 0.1 0.8]
net1=newp([0 2;0 2;0 2;0 2],1,'purelin'); % purelin为输出层传输函数
net2=newp([0 2;0 2;0 2;0 2],1,'logsig');%使用logsig函数激活函数
net3=newp([0 2;0 2;0 2;0 2],1,'tansig');%使用tansig函数激活函数
net4=newp([0 2;0 2;0 2;0 2],1,'hardlim');%使用线性函数激活函数

net1.IW{1}
net2.IW{1}
net3.IW{1}
net4.IW{1}
net1.b{1}
net2.b{1}
net3.b{1}
net4.b{1}


net1.IW{1}=W;
net2.IW{1}=W;
net3.IW{1}=W;
net4.IW{1}=W;

a1=sim(net1,P)
a2=sim(net2,P)
a3=sim(net3,P)
a4=sim(net4,P)

init(net1);
net1.b{1}

运行结果：

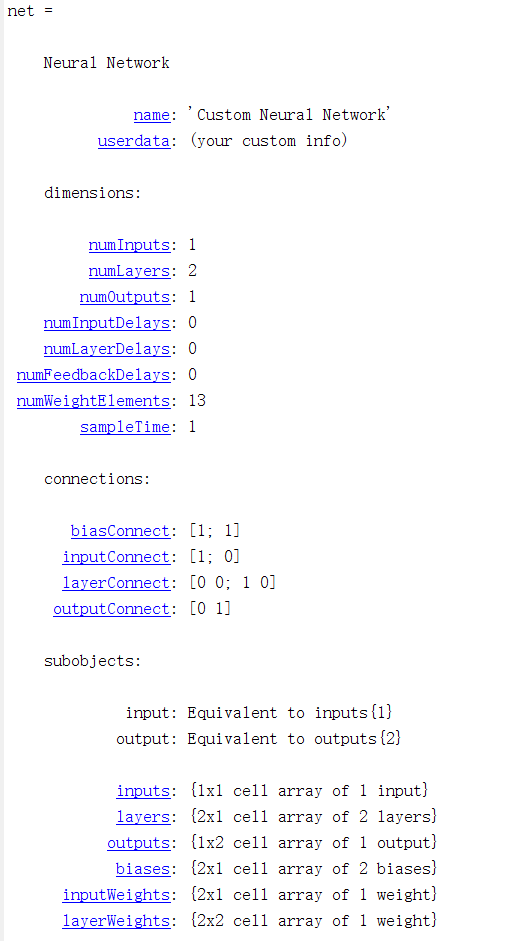
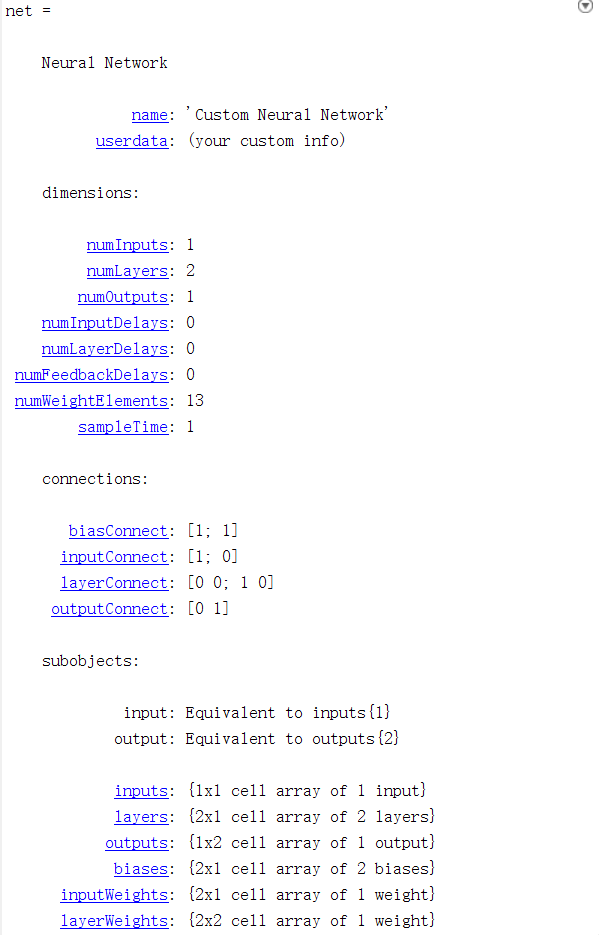
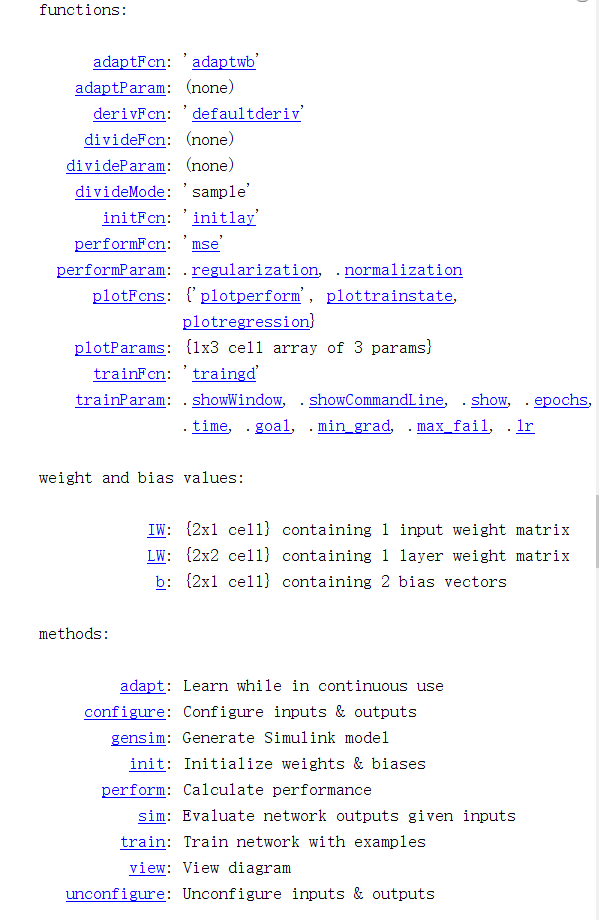
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
(三)训练样本代码
先给出输入数据与输出数据，再构建一个训练网络，再对网络进行训练，对数据仿真预测输出，最后绘图显示数据。
(1）训练样本一

p=[-0.1 0.5]            
t=[-0.3 0.4]            %样本
w_range=-2:0.4:2;
b_range=-2:0.4:2;

ES=errsurf(p,t,w_range,b_range,'logsig');%单输入神经元的误差曲面
plotes(w_range,b_range,ES)%绘制单输入神经元的误差曲面
pause(0.5);
hold off;
net=newp([-2,2],1,'logsig');
net.trainparam.epochs=100;            %最大训练次数
net.trainparam.goal=0.001;            %训练要求精度
figure(2);
[net,tr]=train(net,p,t);              %网络训练
title('动态逼近')
wight=net.iw{1}
bias=net.b
pause;
close;

100次训练相关数据结果：
在这里插入图片描述
分析：Epoch表示迭代次数，此样本中最大次数为100次，Time表示训练时间，Performance为性能指标,此例中为平均绝对误差（mae）（mae为回归模型中一种损失函数）。

函数绘制的误差曲面图：
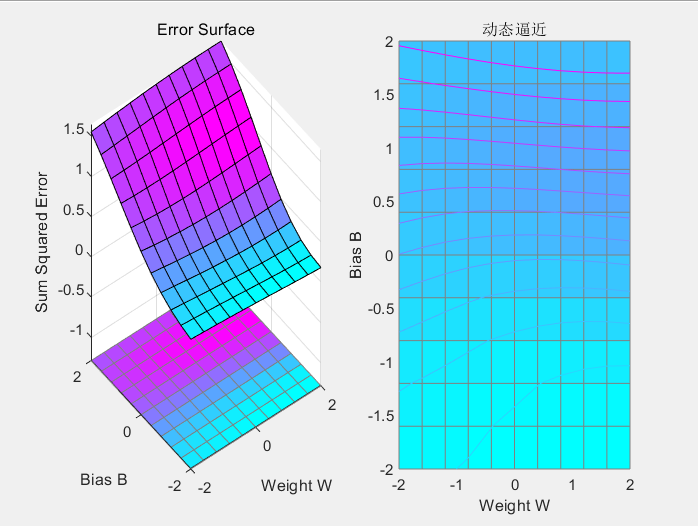
函数绘制的误差曲面图
分析：由errsurf函数计算神经元的误差曲面，并结合权值和阈值确定绘制出误差曲面图。

(2）训练样本二

% 训练
p=[-0.2 0.2 0.3 0.4]          %样本
t=[-0.9 -0.2 1.2 2.0]
h1=figure(1);
net=newff([-2,2],[5,1],{'tansig','purelin'},'trainlm'); %生成神经网络
net.trainparam.epochs=100;             %最大训练次数
net.trainparam.goal=0.0001;            %训练要求精度
net=train(net,p,t);
a1=sim(net,p)
pause;
h2=figure(2);
plot(p,t,'*');
title('样本')
title('样本');
xlabel('Input');
ylabel('Output');
pause;
hold on;
ptest1=[0.2 0.1]
ptest2=[0.2 0.1 0.9]
a1=sim(net,ptest1);     %利用sim函数得到的神经网络仿真
a2=sim(net,ptest2);

net.iw{1}
net.iw{2}
net.b{1} %中间各层神经元阈值
net.b{2} %输出层各神经元阈值

训练结果：
在这里插入图片描述
分析：15次训练后，发现BP神经网络仿真值a1与输出值t已十分接近。

训练数据（训练15次）展示:
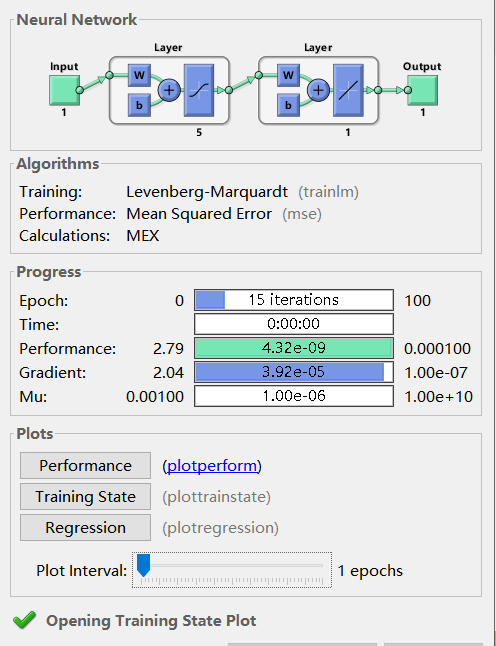
在这里插入图片描述
分析：Neural Network中依次代表的是“输入、隐含层、输出层、输出”，其中隐含层中有5个神经元，Progress中Epoch表示迭代次数，右侧为最大迭代次数100，Performance表示性能，右侧为设定的平均绝对误差，Gradient代表梯度，右侧为设定的梯度，绿色对勾代表性能目标达成。

训练性能分析曲线图：

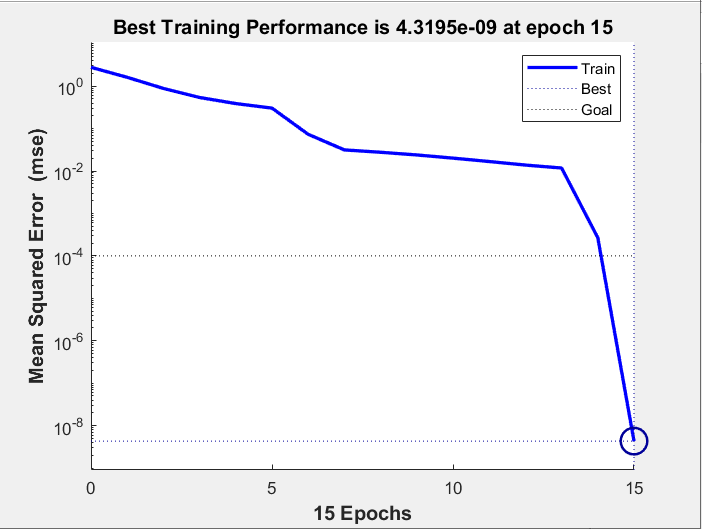
在这里插入图片描述
分析：由图可知，15次训练后，训练结果已十分接近目标值

训练过程其他指标变化图：
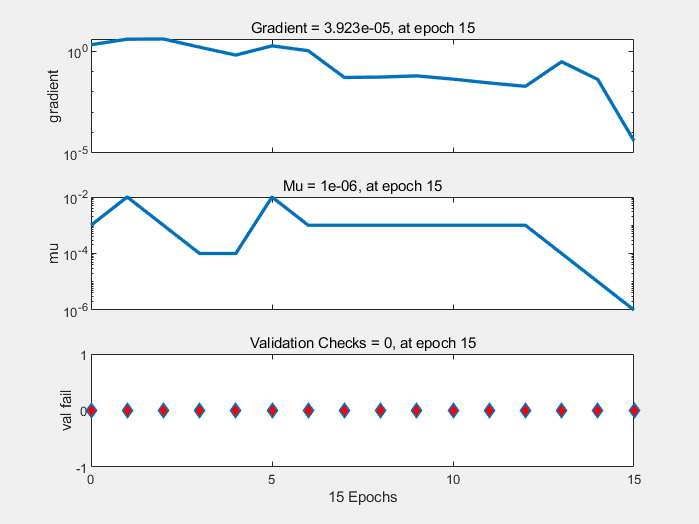
在这里插入图片描述
回归分析图：
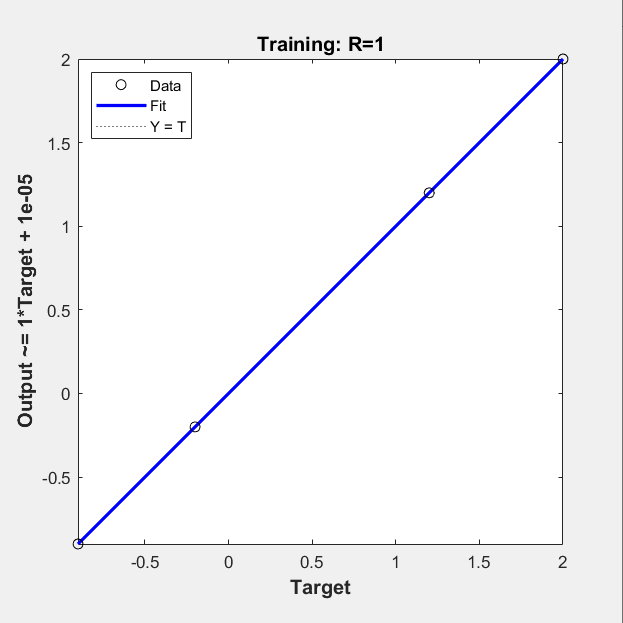
在这里插入图片描述
根据输入输出绘制的样本点图：
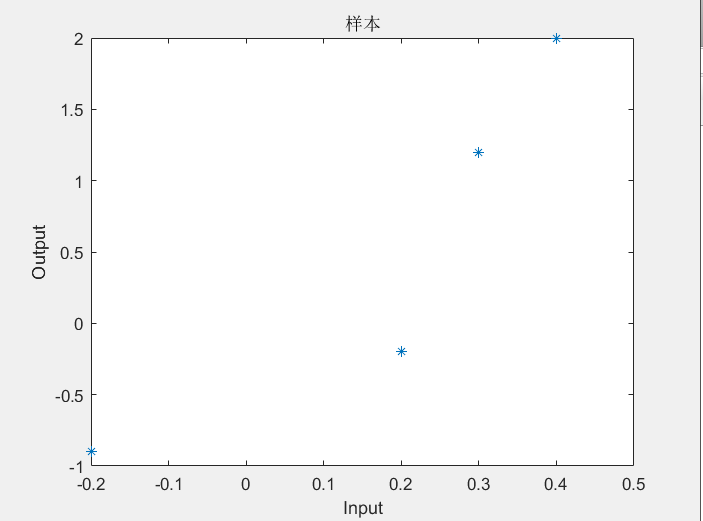
在这里插入图片描述
小结： BP神经网络是目前的主流神经网络学习算法。
优点：

  1. 具有非线性映射能力，理论上可以无限逼近任意复杂函数；
  2. 网络结构简单，计算复杂度低；
  3. 具有较好的容错能力，网络结构部分受损不会对结果产生很大的影响；

缺点：

  1. 权值的初始值会影响训练结果，会出现局部最优解的情况，这就导致很难得到全局最优解。
  2. 激活函数无论对于识别率或收敛速度都有显著的影响。在逼近高次曲线时，S形函数精度比线性函数要高得多，但计算量也要大得多。
  3. 学习率影响着网络收敛的速度，以及网络能否收敛。学习率设置偏小可以保证网络收敛，但是收敛较慢。相反，学习率设置偏大则有可能使网络训练不收敛，影响识别效果。

最后

以上就是搞怪硬币为你收集整理的感知器与BP神经网络的全部内容，希望文章能够帮你解决感知器与BP神经网络所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(43)

相关文章

train
train
基于Matlab的BP神经网络编程过程
基于Matlab的BP神经网络编程过程
bp网络参数说明
bp网络参数说明
神经网络识别仿真实验,神经网络算法实验报告
神经网络识别仿真实验,神经网络算法实验报告
感知器与BP神经网络
感知器与BP神经网络
matlab bestmse,MATLAB中用BP网络算法，performance，training state，regression的图像怎样才算好...
matlab bestmse,MATLAB中用BP网络算法，performance，training state，regression的图像怎样才算好...
神经网络如何识别图像,神经网络和图神经网络
神经网络如何识别图像,神经网络和图神经网络
BP神经网络学习--MATLAB源码详细注释
BP神经网络学习--MATLAB源码详细注释

评论列表共有 0 条评论

立即
投稿
返回
顶部